Bài 45. Đố: Cho 4 đoạn thẳng AB,BC,CD,DA trên giấy kẻ ô vuông như ở hinh 110. Hãy lập luận để giải thích:
a) AB=CD, BC=AD;
b) AB//CD.
Đố. Cho bốn đoạn thẳng AB, BC, CD, DA trên giấy kẻ ô vuông như ở hình 110. Hãy dùng lập luận để giải thích
AB = CD, BC = AD
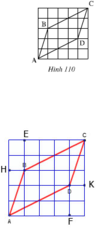
+ ΔAHB và ΔCKD có
HB = KD (=1)
góc AHB = góc CKD(=90º)
AH = CK (=3).
⇒ ΔAHB = ΔCKD(c.g.c)
⇒AB = CD (hai cạnh tương ứng)
+ ΔCEB và ΔAFD có
BE = DF (=2)
góc BEC = góc DFA (=90º)
CE = AF (=4).
⇒ ΔCEB = ΔAFD ( c.g.c)
⇒ BC = AD (hai cạnh tương ứng)
Đố. Cho bốn đoạn thẳng AB, BC, CD, DA trên giấy kẻ ô vuông như ở hình 110. Hãy dùng lập luận để giải thích
AB // CD
ΔABD và ΔCDB có
AB = CD
AD = BC
BD cạnh chung
⇒ ΔABD = ΔCDB (c.c.c)
⇒ góc ABD = góc CDB (hai góc tương ứng)
Vậy AB // CD ( hai gó so le trong bằng nhau )
Cho bốn đoạn thẳng AB, BC, CD, DA trên giấy kẻ ô vuông như ở hình 110. Hãy dùng lập luận để giải thích
a) AB = CD, BC = AD
b) AB // CD
Xét ∆AHB và ∆ CKD có:
HB=KD.
ˆAHB=ˆCKD
AH=CK
=> ∆ AHB = ∆ CKD(c.g.c)
=> AB=CD.( 2 canh tương ứng)
tương tự ∆ CEB = ∆ AFD(c.g.c)
=> BC=AD.
b) ∆ABD và ∆CDB có:
AB=CD(CMT)
BC=AD(CMT)
BD chung.
=> ∆ABD=∆CDB(c.c .c)
=> ˆABD^=ˆCDB( 2 góc tương ứng)
=> AB // CD( hai góc so le trong bằng nhau)
Em bổ sung hình để các bạn giúp nhé
Đố :
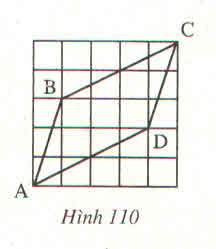
Cho bốn đoạn thẳng AB, BC, CD, DA trên giấy kẻ ô vuông như ở hình 110. Hãy dùng lập luận để giải thích :
a) AB = CD, BC = AD
b) AB // CD
∆AHB và ∆ CKD có:
HB=KD.
AHB^=CKD^
AH=Ck
Nên ∆ AHB = ∆ CKD(c.g.c)
suy ra AB=CD.
tương tự ∆ CEB = ∆ AFD(c.g.c)
suy ra BC=AD.
b) ∆ABD và ∆CDB có:
AB=CD(câu a)
BC=AD(câu a)
BD chung.
Do đó ∆ABD=∆CDB(c.c .c)
Suy ra ˆABD=CDB^
Vậy AB // CD( hai góc so le trong bằng nhau)
Xét ∆AHB và ∆ CKD có:
HB=KD.
ˆAHB=ˆCKD
AH=CK
=> ∆ AHB = ∆ CKD(c.g.c)
=> AB=CD.( 2 canh tương ứng)
tương tự ∆ CEB = ∆ AFD(c.g.c)
=> BC=AD.
b) ∆ABD và ∆CDB có:
AB=CD(CMT)
BC=AD(CMT)
BD chung.
=> ∆ABD=∆CDB(c.c .c)
=> ˆABD^=ˆCDB( 2 góc tương ứng)
=> AB // CD( hai góc so le trong bằng nhau)
Xem thêm tại: http://loigiaihay.com/bai-45-trang-125-sach-giao-khoa-toan-7-tap-1-c42a5103.html#ixzz4nvM2UGda
cho 4 đoạn thẳng như AB BC CD DA trên dấy kẻ ô vuông như như hình 110 (ko vẽ đc) .dùng lập luận để giải thích
AB=CD BC=AD
AB//CD
Bài 45 (SGK tập 1 - trang 125)
Đố :
Cho bốn đoạn thẳng AB, BC, CD, DA trên giấy kẻ ô vuông như ở hình 110. Hãy dùng lập luận để giải thích :
a) AB = CD, BC = AD
b) AB // CD
a)Xét ∆AHB và ∆ CKD có:
HB = KD (= 1 ô)
AHBˆ = CKDˆ
AH = CK (= 3 ô)
=> ∆AHB = ∆CKD(c.g.c)
=> AB = CD (cạnh tương ứng)
Chứng minh tương tự ta đươc: ∆ CEB = ∆ AFD (c.g.c)
suy ra BC=AD.
b) Xét ∆ABD và ∆CDB có:
AB = CD (cmt)
BC = AD (cmt)
BD chung.
=> ∆ABD = ∆CDB (c.c .c)
=> ABDˆ = CDBˆ
Mà hai góc này ở vị trí so le trong
Vậy AB // CD (đpcm)
Bài tập : (bài 45 / trang 125) : Cho bốn đoạn thẳng AB, BC, CD, DA trên giấy kẻ ô vuông như ở hình 110. Hãy dùng lập luận để giải thich :
a. AB = CD, BC = AD.
b. AB // CD.
Hình vẽ thì trong sách nha bạn.
Giải:
a) Xét \(\Delta AHB\) và \(\Delta CKD\) có:
\(HB=KD\)
\(\widehat{AHB}=\widehat{CKD}\)
\(AH=CK\)
Nên \(\Delta AHB=\Delta CKD\left(c.g.c\right)\)
\(\Rightarrow AB=CD\)
Tương tự: \(\Delta CEB=\Delta AFD\left(c.g.c\right)\)
\(\Rightarrow BC=AD\)
b) Xét \(\Delta ABD\) và \(\Delta CDB\) có:
\(AB=CD\left(cmt\right)\)
\(BC=AD\left(cmt\right)\)
\(BD\) là cạnh chung
Nên \(\Delta ABD=\Delta CDB\left(c.c.c\right)\)
\(\Rightarrow\widehat{ABD}=\widehat{CDB}\)
Vậy \(AB\text{ }\) // \(CD\) ( hai góc so le trong bằng nhau )
CHO 4 ĐOẠN THẲNG : AB,BC,CD VÀ DA.TRÊN GIẤY KẺ Ô VUÔNG NHƯ HÌNH DƯỚI. HÃY DÙNG LẬP LUẬN LUẬN ĐỂ GIẢI THÍCH:
A) AB = CD , BC = AD
B) AB SONG SONG VỚI CD
Xét ∆AHB và ∆ CKD có:HB = KD (= 1 ô)AHBˆ = CKDˆAH = CK (= 3 ô)=> ∆AHB = ∆CKD(c.g.c)=> AB = CD (cạnh tương ứng)Chứng minh tương tự ta đươc: ∆ CEB = ∆ AFD (c.g.c)suy ra BC=AD.b) Xét ∆ABD và ∆CDB có:AB = CD (cmt)BC = AD (cmt)BD chung.=> ∆ABD = ∆CDB (c.c .c)=> ABDˆ = CDBˆMà hai góc này ở vị trí so le trongVậy AB // CD (đpcm)
chả bt có khớp ko chứ lười đọc quá