a)Xét ∆AHB và ∆ CKD có:
HB = KD (= 1 ô)
AHBˆ = CKDˆ
AH = CK (= 3 ô)
=> ∆AHB = ∆CKD(c.g.c)
=> AB = CD (cạnh tương ứng)
Chứng minh tương tự ta đươc: ∆ CEB = ∆ AFD (c.g.c)
suy ra BC=AD.
b) Xét ∆ABD và ∆CDB có:
AB = CD (cmt)
BC = AD (cmt)
BD chung.
=> ∆ABD = ∆CDB (c.c .c)
=> ABDˆ = CDBˆ
Mà hai góc này ở vị trí so le trong
Vậy AB // CD (đpcm)
Luyện tập về ba trường hợp bằng nhau của tam giác
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Đố :
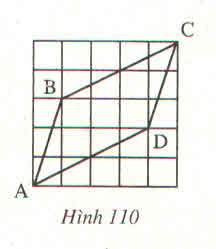
Cho bốn đoạn thẳng AB, BC, CD, DA trên giấy kẻ ô vuông như ở hình 110. Hãy dùng lập luận để giải thích :
a) AB = CD, BC = AD
b) AB // CD
Cho AD // BC và AB // CD. Qua giao điểm M của AC và BD, kẻ một đường thẳng bất kì cắt AD, BC theo thứ tự ở K, E. Chứng minh rằng:
a) AD = BC; b) MA = MC; c) MK = ME
1.Cho tam giác ABC vuông tại A có ABC=1/2 BC. C/m góc B=30 độ 2.Cho điểm M nằm trên đoạn thẳng AB vẽ về 1 phía của AB các tam gác đều AMC và tam gác BMD a)C/M: AD=CB b)Gọi IK theo thứ tự là trung điểm của AD,CD. Tam gác MIK là tam giác gì ?
Cho đoạn thẳng AB. Trên cùng 1 nửa mp AB, vẽ tia Ax và By sao cho BÂx 120 , ABy60.Trên tia By lấy điểm C và trên tia đối của tia Ax lấy điểm D sao cho ADBC.Gọi O là giao điểm của AB và CD
a) C/minh O là trung điểm của mỗi đoạn thẳng AB ; CD
b)Qua O vẽ 1 đường thẳng cắt đường thẳng AD và BC lần lượt ở E và F.C/minh O là trung điểm của EF
c)Gọi M ; N lần lượt là trung điểm của AD, BC. C/minh O là trung điểm của MN
Mik đang cần rất gấp, mong mấy bạn giải dùm mik ( giải chi tiết ra hộ mik nha)
Đọc tiếp
Cho đoạn thẳng AB. Trên cùng 1 nửa mp AB, vẽ tia Ax và By sao cho BÂx= 120 , ABy=60.Trên tia By lấy điểm C và trên tia đối của tia Ax lấy điểm D sao cho AD=BC.Gọi O là giao điểm của AB và CD
a) C/minh O là trung điểm của mỗi đoạn thẳng AB ; CD
b)Qua O vẽ 1 đường thẳng cắt đường thẳng AD và BC lần lượt ở E và F.C/minh O là trung điểm của EF
c)Gọi M ; N lần lượt là trung điểm của AD, BC. C/minh O là trung điểm của MN
Mik đang cần rất gấp, mong mấy bạn giải dùm mik ( giải chi tiết ra hộ mik nha)
Hai đoạn thẳng AB và CD có chung trung điểm I . Chứng minh :
a. Hai tam giác ACI và BDI bằng nhau
b. AC = BD và AD = BC
c. AC // BD và AD // BC
Cho 2 đoạn thẳng AB//CD và AB=CD.(B,C cùng thuộc nửa mp bờ AD). Gọi O là giao điểm của AC và BD. chứng minh:
a)o là trung điểm của AC và BD.
b)AD//BC
c)Kẻ BH vuông góc với AC, DK vuông góc với AC. CM: tam giác ABH=tam giác CDK.
d) BK=DH và BK//BH.
e) Trên AB,CD lần lượt lấy các điểm M và N sao cho BM=DN. CM m,o,n thẳng hàng
Cho tam giác ABC. Từ A, kẻ đường thẳng song song với BC. Từ C, kẻ đường thẳng song song với AB. Hai đường thẳng này cắt nhau tại D.
a, Cm ADBC và ABCD
b, Gọi O là giao của AC và BD. Cm O là trung điểm của AC và BD.
c, Qua O, kẻ đg thẳng bất kì cắt 2 đg thẳng AB và CD lần lượt ở M và N. Cm O là trung điểm của MN.
Giúp mk mọi người ơi!!! Câu a mk làm đc rồi nha!!! Làm câu b và c giúp mk!!! Mk cảm ơn!!!
Đọc tiếp
Cho tam giác ABC. Từ A, kẻ đường thẳng song song với BC. Từ C, kẻ đường thẳng song song với AB. Hai đường thẳng này cắt nhau tại D.
a, Cm AD=BC và AB=CD
b, Gọi O là giao của AC và BD. Cm O là trung điểm của AC và BD.
c, Qua O, kẻ đg thẳng bất kì cắt 2 đg thẳng AB và CD lần lượt ở M và N. Cm O là trung điểm của MN.
Giúp mk mọi người ơi!!! Câu a mk làm đc rồi nha!!! Làm câu b và c giúp mk!!! Mk cảm ơn!!!
Cho tam giác ABC có AB =AC . Gọi M là trung điểm của đoạn thẳng BC .
a) Chứng minh rằng ΔABM =ΔACM .
b) Trên tia đối của tia MA lấy điểm D sao cho MD = MA . Chứng minh rằng AB // CD .
c) Gọi I là trung điểm của đoạn thẳng BD . Trên tia đối của tia IC lấy điểm E sao cho
IE =IC . Chứng minh rằng A B E , thẳng hàng.
Cho tam giác ABC. M là trung điểm của AC. Trên tia đối của tia MB lấy điểm D sao cho BM MD.
a) Chứng minh: Tam giác AMD Tam giác CMB
b) Chứng minh: AB // CD
c) Vẽ CN vuông góc với AD (N in AD) và AP vuông góc với BC ( P in BC) Chứng minh: NDBP
d) Chứng minh: N, M, P thẳng hàng
Đọc tiếp
Cho tam giác ABC. M là trung điểm của AC. Trên tia đối của tia MB lấy điểm D sao cho BM = MD.
a) Chứng minh: Tam giác AMD = Tam giác CMB
b) Chứng minh: AB // CD
c) Vẽ CN vuông góc với AD (N \(\in\) AD) và AP vuông góc với BC ( P \(\in\) BC) Chứng minh: ND=BP
d) Chứng minh: N, M, P thẳng hàng














