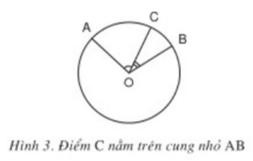
Hãy chứng minh đẳng thức số đo A B ⏜ = sđ A C ⏜ + sđ C B ⏜ trong trường hợp điểm C nằm trên cung nhỏ AB (h.3).
Với ba số a, b, c không âm, chứng minh bất đẳng thức: a + b + c ≥ a b + b c + c a . Hãy mở rộng kết quả cho trường hợp bốn số, năm số không âm.
Cho a/b=c/d. Hãy chứng minh đẳng thức sau:
(a+b)^2/(c+d)^2=ab/cd
Có: a/b=c/d => a/c=b/d
=>(a+b)/(c+d)=a/c
=>(a+b)^2/(c+d)^2=(a/c)^2=a/c.b/d=ab/cd
=> dpcm
Cho a, b, c, p lần lượt là số đo các cạnh và nửa chu vi của một tam giác.
Chứng minh: 1/p-a + 1/p-b + 1/p-c >= 2(1/a + 1/b + 1/c)
Đẳng thức sảy ra khi nào?
Ta sẽ áp dụng BĐT sau vào bài tập này \(\frac{a^2}{m}+\frac{b^2}{n}+\frac{c^2}{p}\le\frac{\left(a+b+c\right)^2}{m+n+p}\)dấu "=" xảy ra khi \(\frac{a}{m}=\frac{b}{n}=\frac{c}{p}\)
Ta có \(p-a=\frac{a+b+c}{2}-a=\frac{a+b+c-2a}{2}\)\(\Leftrightarrow\)\(p-a=\frac{b+c-a}{2}\)
\(\Leftrightarrow\)\(\frac{1}{p-a}=\frac{2}{b+c-a}\).Tương tự\(\frac{1}{p-b}=\frac{2}{a+c-b}\);\(\frac{1}{p-c}=\frac{2}{b+a-c}\)
nên \(\frac{1}{p-a}+\frac{1}{p-b}+\frac{1}{p-c}=2\left(\frac{1}{b+c-a}+\frac{1}{c+a-b}+\frac{1}{a+b-c}\right)\)
Áp dụng BĐT trên ta có \(\frac{1}{b+c-a}=\frac{\left(1+1-1\right)^2}{b+c-a}\ge\frac{1}{c}+\frac{1}{b}-\frac{1}{a}\);\(\frac{1}{a+c-b}\ge\frac{1}{a}+\frac{1}{c}-\frac{1}{b}\);\(\frac{1}{a+b-c}\ge\frac{1}{a}+\frac{1}{b}-\frac{1}{c}\)
Vậy \(\frac{1}{p-a}+\frac{1}{p-b}+\frac{1}{p-c}\ge2\left(\frac{1}{c}+\frac{1}{b}+\frac{1}{a}\right)\)
Kết bạn với mình có gì tiện hỏi nhau nha có gì khó cứ gửi
bài này cũng gần giống nè giúp mk vs
cho a b c là độ dài 3 cạnh tam giác p là nửa chu vi ab/(p-c) + bc/(p-a) + ca/(p-b)>=4p
đây là toán lớp 8 hôm qua cô vừa dạy xog này dễ v
Chứng minh bất đẳng thức cô-si với 3 số a,b,c không âm: \(\dfrac{a+b+c}{3}\ge\sqrt[3]{abc}\). Dấu đẳng thức xảy ra khi a=b=c.
Áp dụng chứng minh bất đẳng thức: \(\left(a+b+c\right)\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge9\)
Bạn tham khảo cách chứng minh tại đây :
Câu hỏi của Nguyễn Huy Thắng - Toán lớp 10 | Học trực tuyến
Áp dụng : Theo BĐT \(AM-GM\) ta có :
\(a+b+c\ge3\sqrt[3]{abc}\)
\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge3\sqrt[3]{\dfrac{1}{abc}}\)
Nhân vế theo vế ta được :
\(\left(a+b+c\right)\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge3\sqrt[3]{abc}.3\sqrt[3]{\dfrac{1}{abc}}=3.3.1=9\)
Dấu \("="\) xảy ra khi \(a=b=c\)
Với 3 số a, b, c không âm, chứng minh bất đẳng thức \(a+b+c\ge\sqrt{ab}+\sqrt{bc}+\sqrt{ca}\)
Hãy mở rộng kết quả cho trường hợp bốn số, năm số không âm
Áp dụng bất đẳng thức Cô-si cho hai số không âm, ta có :
\(\dfrac{a+b}{2}\ge\sqrt{ab}\) (1)
\(\dfrac{b+c}{2}\ge\sqrt{bc}\) (2)
\(\dfrac{c+a}{2}\ge\sqrt{ca}\) (3)
Cộng từng vế bất đẳng thức (1), (2), (3) ta được :
\(a+b+c\ge\sqrt{ab}+\sqrt{bc}+\sqrt{ca}\)
Vậy bất đẳng thức đã được chứng minh
Mở rộng cho bốn số a, b, c, d không âm, ta có bất đẳng thức :
\(a+b+c+d\ge\sqrt{ab}+\sqrt{bc}+\sqrt{cd}+\sqrt{da}\)
Mở rộng cho năm số a, b, c, d, e không âm, ta có bất đẳng thức : \(a+b+c+d+e\ge\sqrt{ab}+\sqrt{bc}+\sqrt{cd}+\sqrt{de}+\sqrt{ea}\)
áp dụng BĐT AM-GM với 2 số không âm
\(a+b\ge2\sqrt{ab}\)
\(b+c\ge2\sqrt{bc}\)
\(a+c\ge2\sqrt{ac}\)
cộng các vế của BĐT ta có
\(2\left(a+b+c\right)\ge2\left(\sqrt{ab}+\sqrt{bc}+\sqrt{ac}\right)\)
chia cả hai vế của BĐT cho 2 ta có đpcm
Trên đường tròn tâm O đường kính AB=2R , lấy điểm C sao cho sđ cung BC=60° . Hai tiếp tuyến với đường tròn vẽ từ B và C cắt nhau tại D .
a) Tính sđ góc BOC và sđ cung nhỏ AC .
b) chứng minh tứ giác OBDC nội tiếp .
c) Tia AC cắt tia BD tại E . Chứng minh D là trung điểm của BE .
d) Biết R=15cm . Tính diện tích hình quạt giới hạn bởi cung nhỏ AC( biết π=3,14)
Với ba số a, b, c không âm, chứng minh bất đẳng thức \(a+b+c\ge\sqrt{ab}+\sqrt{bc}+\sqrt{ca}\)
Hãy mở rộng kết quả cho trường hợp bốn số, năm số không âm
áp dụng bất đẳng thức cô- si, ta có:
\(a+b\ge2\sqrt{ab}\) \(\left(1\right)\)
\(b+c\ge2\sqrt{bc}\) \(\left(2\right)\)
\(c+a\ge2\sqrt{ca}\) \(\left(3\right)\)
Cộng (1),(2),(3) vế theo vế, ta được:
\(2\left(a+b+c\right)\ge2\left(\sqrt{ab}+\sqrt{bc}+\sqrt{ca}\right)\)
\(\Leftrightarrow\) \(a+b+c\ge\sqrt{ab}+\sqrt{bc}+\sqrt{ca}\)
Dấu " = " xảy ra <=> \(a=b=c\)
chứng minh đẳng thức a(b-c)-a(b+d)=-a(c+d)
ta có:a(b−c)−a(b+d)=−a(c+d)
VT(vế trái)=a(b−c)−a(b+d)
=ab−ac−ab−ad
=(ab−ab)−ac−ad
=0−a(c+d)
=−a(c+d)=VP(vế phải)
\(a\left(b-c\right)-a\left(b+d\right)\)
\(=a\left(b-c-b-d\right)\)
\(=a\left(-c-d\right)\)
\(=-a\left(c+d\right)\left(dpcm\right)\)
Ta có: a(b-c)-a(b+d)
=ab-ac-ab-ad
=-ac-ad=-(ac+ad)=-a(c+d)
Vì -a(c+d)=-a(c+d) nên a(b-c)-a(b+d)=-a(c+d)
Chứng minh bất đẳng thức (a + 1)2 ≥ 4a
Chứng minh : (ac + bd)2 + (ad – bc)2 = (a2 + b2)(c2 + d2)
Cho a, b, c là các số dương. Chứng minh : a3 + b3 + abc ≥ ab(a + b + c)
Mn giúp mik vs ;-;
a: \(\Leftrightarrow\left(a+1\right)^2-4a\ge0\)
hay \(\left(a-1\right)^2>=0\)(luôn đúng)
b: \(VT=a^2c^2+2abcd+b^2d^2+a^2d^2-2abcd+b^2c^2\)
\(=a^2\left(c^2+d^2\right)+b^2\left(c^2+d^2\right)\)
\(=\left(c^2+d^2\right)\left(a^2+b^2\right)=VP\)