Tứ giác ABCD có góc ABC + góc ADC = 180o. Chứng minh rằng các đường trung trực của AC, BD, AB cùng đi qua một điểm.

Những câu hỏi liên quan
Tứ giác ABCD có góc A B C + g ó c A D C = 180 o . Chứng minh rằng các đường trung trực của AC, BD, AB cùng đi qua một điểm
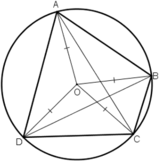
Tứ giác ABCD có 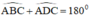
⇒ ABCD là tứ giác nội tiếp
Gọi O là tâm đường tròn ngoại tiếp tứ giác ABCD
⇒ OA = OB = OC = OD = R
Do OA= OC nên ΔOAC cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác. Suy ra, O thuộc đường trung trực của AC.
Do OB= OD nên ΔOBD cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác. Suy ra, O thuộc đường trung trực của BD
Do OA= OB nên ΔOAB cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác. Suy ra, O thuộc đường trung trực của AB.
⇒ O thuộc đường trung trực của AC, BD, AB .
Vậy các đường trung trực của AC, BD, AB cùng đi qua O.
Đúng 0
Bình luận (0)
- Tứ giác ABCD có \(\widehat{ABC}+\widehat{ADC}=180^o\)mà hai góc ABC và ADC là 2 góc ở vị trí đối nhau
=> Tứ giác ABCD là tứ giác nội tiếp
- Gọi O là tâm của đường tròn ngoại tiếp tứ giác ABCD , khi đó OA = OB = OC = OD ( cùng bán kính của đường tròn ( O ))
+) Vì OA = OB nên O thuộc đường trung trực của đoạn thằng AB
+) Vì OA = OC nên O thuộc đường trung trực của đoạn thẳng AC
+) VÌ OD = OB nên O thuộc đường trung trực của đoạn thằng BD
Do đó các đường trung trực của AB , BD cùng đi qua tâm O của đường tròn ngoại tiếp tứ giác ABCD
Tứ giác ABCD có \(\widehat{ABC}+\widehat{ADC}=180^o.\) Chứng minh rằng các đường trung trực của AC, BD, AB cùng đi qua một điểm.
Tứ giác ABCD có tổng hai góc đối diện bằng 180o nên nội tiếp đường tròn tâm O, ta có
OA = OB = OC = OD
Do đó các đường trung trực của AB, BD, AB cùng đi qua O
Đúng 0
Bình luận (0)
Tứ giác ABCD có tổng hai góc đối diện bằng 180o nên nội tiếp đường tròn tâm O, ta có
OA = OB = OC = OD
Do đó các đường trung trực của AB, BD, AB cùng đi qua O
Đúng 0
Bình luận (0)
Tứ giác ABCD có tổng hai góc đối diện =180 độ nên nối tiếp đường tròn tâm O,ta có OA=OB=OC=OD
Do đó các đường trung trực của AB,BD,AC cùng đi qua O
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có AB = AD, BC = CD
a) Chứng minh rằng AC là đường trung trực của đoạn thẳng BD.
b) Biết góc BDA= 110°, góc BCD= 50°. Tính góc ABC, góc ADC.
c) Gọi I là giao điểm của AC và BD, chứng minh ∆ABI = ∆ADI
Cho tam giác ABC có AB=AC. Trên các cạnh AB và AC lấy các điểm D và E sao cho BD=CE. Gọi K là giao điểm của BE và CD.
a) Chứng minh rằng tam giác ADC = tam giác AEB
b) Chứng minh ba đường trung trực của tam giác ABC và trung trực của DE cùng đi qua một điểm
a: Xét ΔADC và ΔAEB có
AD=AE
góc A chung
AC=AB
=>ΔADC=ΔAEB
b: Gọi giao của 3 đường trung trực trong ΔABC là O
=>OB=OC
Kẻ OK vuông góc BC, OK cắt DE tại M
=>OK là trung trực của BC
Xét ΔABC có AD/AB=AE/AC
nên DE//BC
=>OM vuông góc DE tạiM
Xét ΔOBD và ΔOCE có
OB=OC
góc OBD=góc OCE
BD=CE
=>ΔOBD=ΔOCE
=>OE=OD
=>OM là trung trực của DE
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có AB = AD, BC = CD
a) Chứng minh rằng AC là đường trung trực của đoạn thẳng BD.
b) Biết góc BDA = 110°, góc BCD = 50°. Tính góc ABC, ADC.
c) Gọi I là giao điểm của AC và BD, chứng minh ∆ABI = ∆ADI
a: Ta có: AB=AD
nên A nằm trên đường trung trực của BD(1)
Ta có: CB=CD
nên C nằm trên đường trung trực của BD(2)
Từ (1) và (2) suy ra AC là đường trung trực của BD
c: Xét ΔABI vuông tại I và ΔADI vuông tại I có
AB=AD
AI chung
Do đó; ΔABI=ΔADI
Đúng 0
Bình luận (0)
cho tứ giác abcd có đường chéo bd đồng thời là phân giác của góc ABC và ADC . Chứng minh BD là trung trực của AC
Xét ΔABD và ΔCBD có
góc ABD=góc CBD
BD chung
góc ADB=góc CDB
=>ΔABD=ΔCBD
=>AB=CB và DA=DC
=>BD là trung trực của AC
Đúng 0
Bình luận (1)
giúp mình bài này với!Bài 1: Cho tứ giác ABCD có ABAD, CBCD, góc C 60o , góc A100o a, Chứng minh AC là đường trung trực của BD.b, Tính góc B và góc D.Bài 3: Cho tứ giác ABCD có B +D180o , CBCD. Trên tia đối của tia DA lấy điểm E, phân giác ngoài góc A và góc B cắt tại F. Chứng minh AEBC+D2C+D2 và AFBA+B/2Bài 4: Cho tứ giác ABCD có B+D180o , CBCD. Trên tia đối của tia DA lấy điểm E sao cho DEAB. Chứng minh:a, △ABC và △EDC bằng nhaub, AC là phân giác của góc ABài 5: Cho tứ giác ABCD biết số đo của...
Đọc tiếp
giúp mình bài này với!
Bài 1: Cho tứ giác ABCD có AB=AD, CB=CD, góc C =60o , góc A=100o
a, Chứng minh AC là đường trung trực của BD.
b, Tính góc B và góc D.
Bài 3: Cho tứ giác ABCD có <B +<D=180o , CB=CD. Trên tia đối của tia DA lấy điểm E, phân giác ngoài góc A và góc B cắt tại F. Chứng minh <AEB=<C+<D2<C+<D2 và <AFB=<A+<B/2
Bài 4: Cho tứ giác ABCD có <B+<D=180o , CB=CD. Trên tia đối của tia DA lấy điểm E sao cho DE=AB. Chứng minh:
a, △ABC và △EDC bằng nhau
b, AC là phân giác của góc A
Bài 5: Cho tứ giác ABCD biết số đo của các góc A,B,C,D tỉ lệ thuận với 5,8,13,10.
a, Tính số đo các góc của tứ giác ABCD.
b,Kéo dài hai cạnh AB và CD cắt nhau tại E, kéo dài hai cạnh AD và BC cắt nhau tại F. Hai tia phân giác của góc AED và góc AFB cắt nhau tại O. Phân giác góc AFB cắt cạnh CD VÀ AB lần lượt là M và N. CM: O là trung điểm đoạn MN.
Bài 1:
a: Ta có: AB=AD
nên A nằm trên đường trung trực của BD(1)
Ta có: CB=CD
nên C nằm trên đường trung trực của BD(2)
Từ (1) và (2) suy ra AC là đường trung trực của BD
b: Xét ΔBAC và ΔDAC có
AB=AD
AC chung
BC=DC
Do đó: ΔBAC=ΔDAC
Suy ra: \(\widehat{B}=\widehat{D}\)
=>\(\widehat{B}=\widehat{D}=\dfrac{200^0}{2}=100^0\)
Đúng 0
Bình luận (0)
giúp mình bài này với!Bài 1: Cho tứ giác ABCD có ABAD, CBCD, góc C 60o , góc A100o a, Chứng minh AC là đường trung trực của BD.b, Tính góc B và góc D.Bài 3: Cho tứ giác ABCD có B +D180o , CBCD. Trên tia đối của tia DA lấy điểm E, phân giác ngoài góc A và góc B cắt tại F. Chứng minh AEBdfrac{ C+ D}{2} và AFBA+B/2Bài 4: Cho tứ giác ABCD có B+D180o , CBCD. Trên tia đối của tia DA lấy điểm E sao cho DEAB. Chứng minh:a, △ABC và △EDC bằng nhaub, AC là phân giác của góc ABài 5: Cho tứ giác ABCD biết số...
Đọc tiếp
giúp mình bài này với!
Bài 1: Cho tứ giác ABCD có AB=AD, CB=CD, góc C =60o , góc A=100o
a, Chứng minh AC là đường trung trực của BD.
b, Tính góc B và góc D.
Bài 3: Cho tứ giác ABCD có <B +<D=180o , CB=CD. Trên tia đối của tia DA lấy điểm E, phân giác ngoài góc A và góc B cắt tại F. Chứng minh <AEB=\(\dfrac{< C+< D}{2}\) và <AFB=<A+<B/2
Bài 4: Cho tứ giác ABCD có <B+<D=180o , CB=CD. Trên tia đối của tia DA lấy điểm E sao cho DE=AB. Chứng minh:
a, △ABC và △EDC bằng nhau
b, AC là phân giác của góc A
Bài 5: Cho tứ giác ABCD biết số đo của các góc A,B,C,D tỉ lệ thuận với 5,8,13,10.
a, Tính số đo các góc của tứ giác ABCD.
b,Kéo dài hai cạnh AB và CD cắt nhau tại E, kéo dài hai cạnh AD và BC cắt nhau tại F. Hai tia phân giác của góc AED và góc AFB cắt nhau tại O. Phân giác góc AFB cắt cạnh CD VÀ AB lần lượt là M và N. CM: O là trung điểm đoạn MN.
cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau. Gọi E, F lần lượt là trung điểm của AB, BC. Chứng minh rằng đường thẳng đi qua E vuông góc với CD, đường thẳng đi qua F vuông góc với AD và một trong hai đường chéo đồng quy



















