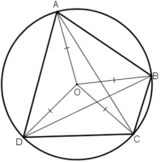
Tứ giác ABCD có 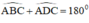
⇒ ABCD là tứ giác nội tiếp
Gọi O là tâm đường tròn ngoại tiếp tứ giác ABCD
⇒ OA = OB = OC = OD = R
Do OA= OC nên ΔOAC cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác. Suy ra, O thuộc đường trung trực của AC.
Do OB= OD nên ΔOBD cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác. Suy ra, O thuộc đường trung trực của BD
Do OA= OB nên ΔOAB cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác. Suy ra, O thuộc đường trung trực của AB.
⇒ O thuộc đường trung trực của AC, BD, AB .
Vậy các đường trung trực của AC, BD, AB cùng đi qua O.
Kiến thức áp dụng
+ Nếu một tứ giác có tổng số đo hai góc đối nhau bằng 180º thì tứ giác đó nội tiếp một đường tròn.










