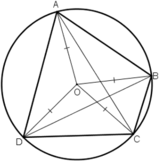
Tứ giác ABCD có 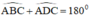
⇒ ABCD là tứ giác nội tiếp
Gọi O là tâm đường tròn ngoại tiếp tứ giác ABCD
⇒ OA = OB = OC = OD = R
Do OA= OC nên ΔOAC cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác. Suy ra, O thuộc đường trung trực của AC.
Do OB= OD nên ΔOBD cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác. Suy ra, O thuộc đường trung trực của BD
Do OA= OB nên ΔOAB cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác. Suy ra, O thuộc đường trung trực của AB.
⇒ O thuộc đường trung trực của AC, BD, AB .
Vậy các đường trung trực của AC, BD, AB cùng đi qua O.
- Tứ giác ABCD có \(\widehat{ABC}+\widehat{ADC}=180^o\)mà hai góc ABC và ADC là 2 góc ở vị trí đối nhau
=> Tứ giác ABCD là tứ giác nội tiếp
- Gọi O là tâm của đường tròn ngoại tiếp tứ giác ABCD , khi đó OA = OB = OC = OD ( cùng bán kính của đường tròn ( O ))
+) Vì OA = OB nên O thuộc đường trung trực của đoạn thằng AB
+) Vì OA = OC nên O thuộc đường trung trực của đoạn thẳng AC
+) VÌ OD = OB nên O thuộc đường trung trực của đoạn thằng BD
Do đó các đường trung trực của AB , BD cùng đi qua tâm O của đường tròn ngoại tiếp tứ giác ABCD











