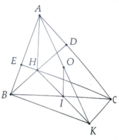
Cho tam giác ABC (AB < AC) có hai đường cao BD và CE cắt nhau tại trực tâm H. Lấy I là trung điểm của BC
a, Gọi K là điểm đối xứng của H qua I. Chứng minh tứ giác BHCK là hình bình hành
b, Xác định tâm O của đường tròn qua các điểm A, B, K, C
c, Chứng minh OI và AH song song
d, Chứng minh BE.BA + CD.CA = B C 2
a, BHCK có I là trung điểm hai đường chéo
b, Ta có ∆ABK, ∆ACK vuông tại B và C nên A,B,K,C nằm trên đường tròn đường kính AK
c, Ta có OI là đường trung bình của ∆AHK => OI//AH
d, Gọi AH cắt BC tại M. Ta có BE.BA = BM.BC và CA.CD = CM.BC => ĐPCM












