Một vật dao động điều hòa với phương trình: x = 6 cos 2 ( 4 π t + π / 6 ) cm. Quãng đường vật đi được trong 0,125 s kể từ thời điểm t = 0 là:
A. 6cm
B. 4,5cm
C. 7,5cm
D. 9cm
Một vật nhỏ dao động điều hòa có phương trình x = 6 cos ( ωt + π 2 ) cm
Pha ban đầu của dao động là:
A. 0 , 25 π rad.
B. π rad.
C. 1 , 5 π rad.
D. 0 , 5 π rad.
Đán án D
+ Pha ban đầu của dao động là 0 , 5 π
\(A^2=x^2+\dfrac{v^2}{\omega^2}\Leftrightarrow16=x^2+\dfrac{\left(20\sqrt{2}\right)^2.10}{10^2.10}\Rightarrow x=\pm2\sqrt{2}\left(cm\right)=\pm\dfrac{\sqrt{2}}{2}A\)
\(\Rightarrow\varphi=\dfrac{\pi}{4}+\dfrac{\pi}{2}\Rightarrow t=\dfrac{3\pi}{4.10\pi}=0,075\left(s\right)\)
: Một vật tham gia đồng thời 2 dao động điều hòa cùng phương ,cùng tần số với các phương trình x1=5cos(20pt - 3ᴫ/4) cm và x2 = 10 cos(20pt + ᴫ/4) cm
a/ X/định phương trình dao động tổng hợp .
b/ X/định v? Của vật khi vật qua vị trí có li độ x= xmax/2 .
a/ Sử dụng máy tính để tổng hợp pt cho lẹ, cơ mà mt mình ko có nên mình xài tay, bạn check lại bằng mt hộ mình
\(x=x_1+x_2=5\left[\cos\left(20\pi t-\dfrac{3\pi}{4}\right)+2\cos\left(20\pi t+\dfrac{\pi}{4}\right)\right]\)
\(\cos\left(20\pi t-\dfrac{3}{4}\pi\right)=-\cos\left(20\pi t+\dfrac{\pi}{4}\right)\Rightarrow x=5\cos\left(20\pi t+\dfrac{\pi}{4}\right)\left(cm\right)\)
b/ \(x=\dfrac{A}{2}\Rightarrow v=\pm\omega\sqrt{A^2-\dfrac{A^2}{4}}=\pm20\pi\sqrt{25-\dfrac{25}{4}}=\pm50\pi\sqrt{3}\left(cm/s\right)\)
Một vật dao động điều hòa có phương trình x = 4 cos(10πt + π/6) cm. Tại thời điểm t = 0 vật có tọa độ bằng bao nhiêu?
Một vật dao động điều hòa với phương trình x = 5 cos ( 10 πt ) Xác định chu kì, tần số dao động chất điểm:
A. f = 10 Hz, T = 0,1s
B. f = 5 Hz, T= 0,2s.
C. f = 5 π Hz , T = 0 , 2 s
D. f = 0.2Hz, T = 5s
Tần số và chu kì của con lắc là f = 5 Hz, T = 0,2 s
Đáp án B
Câu 1 : Một vật thực hiện hai dao động điều hòa với phương trình lần lượt là X1 = 4 cos 6 p t + p trên 3 x 2 = 5 + 6 t + t p cm Hãy xác định vận tốc cực đại mà dao động có thể đạt được #Giup em với ạ cần lắm
Một vật dao động điều hòa dọc theo trục Ox với phương trình vận tốc là overline v = 16π cos(4πt - π/6) cm/ s . Xác định thời điểm lần thứ 2023 vật chuyển động nhanh dần qua vị trí x =2 kể từ lúc bắt đầu dao động
Từ pt \(v=16\pi\cos\left(4\pi t-\dfrac{\pi}{6}\right)=16\pi\cos\left(4\pi t-\dfrac{2\pi}{3}+\dfrac{\pi}{2}\right)\) (cm/s), ta suy ra \(\omega=4\pi\left(rad/s\right)\), lại có \(\omega A=16\pi\Leftrightarrow A=\dfrac{16\pi}{\omega}=4\left(cm\right)\)
\(\varphi_0=-\dfrac{2\pi}{3}\); \(T=\dfrac{2\pi}{\omega}=0,5\left(s\right)\)
Đường tròn lượng giác:
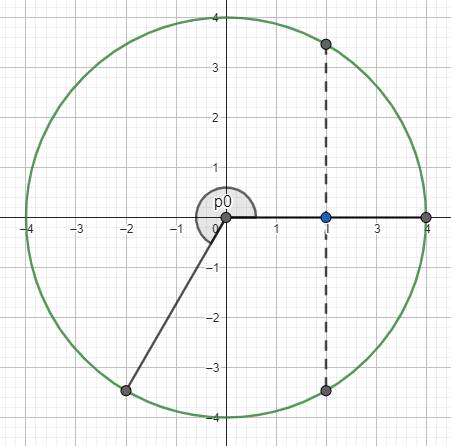
Từ đây, ta có thể thấy tại thời điểm lần thứ 2023 vật chuyển động qua vị trí \(x=2\) kể từ khi dao động, góc quét của vật là \(\Delta\varphi=\dfrac{\pi}{3}+1011.2\pi=\dfrac{6067}{3}\pi\) (rad)
Thời điểm lần thứ 2023 vật chuyển động qua vị trí \(x=2\) kể từ lúc bắt đầu dao động là \(\Delta t=\dfrac{\Delta\varphi}{2\pi}.T=\dfrac{\dfrac{6067}{3}\pi}{2\pi}.0,5=\dfrac{6067}{12}\approx505,58\left(s\right)\)
một vật dao động điều hòa theo phương trình x=4*cos(4*pi*t-pi/6). Kể từ khi vật bắt đầu dao động, vận tốc và gia tốc có giá trị dương trong khoảng thời gian ngắn nhất như thế nào
Vận tốc dương khi vật chuyển động theo chiều dương trục toạ độ.
Gia tốc có hướng về VT cân bằng, nên để gia tốc dương thì vật đi từ biên độ âm về VTCB.
Do vậy, vận tốc và gia tốc đều có giá trị dương khi vật đi từ biên độ âm về VTCB.
Thời gian ngắn nhất là 1/4 T.
Một vật dao động điều hòa theo phương trình: \(x=4\cos\left(6\pi t+\dfrac{\pi}{6}\right)\left(cm\right)\). Vận tốc của vật đạt giá trị \(12\pi\) (cm/s) khi vật đi qua li độ
\(v=x'=6pi\cdot4\cdot cos\left(6pi\cdot t+\dfrac{pi}{6}+\dfrac{pi}{2}\right)\)
\(=24pi\cdot cos\left(6pi\cdot t+\dfrac{2}{3}pi\right)\)
v'=12pi
=>cos(6pi*t+2/3pi)=1/2
=>6pi*t+2/3pi=pi/3+k2pi hoặc 6pi*t+2/3pi=-pi/3+k2pi
=>6pi*t=-1/3pi+k2pi hoặc 6pi*t=-pi+k2pi
=>t=-1/18+k/3 hoặc t=-1/6+k/3
Một vật dao động điều hòa dọc theo trục Ox với phương trình dao động là x = 4 cos ( 2 πt - π / 3 ) cm (t tính bằng s). Lấy π 2 = 10 . Gia tốc của vật khi có li độ bằng 3 cm là
A. ‒12 cm/s2
B. 120 cm/s2
C. ‒1,2 cm/s2
D. ‒60 cm/s2