Tìm tất cả các giá trị của tham số m để phương trình: 1 3 cos 3 x - 3 cos 2 x + 5 cos x - 3 + 2 m = 0 có đúng bốn nghiệm thuộc đoạn 0 ; 2 π
A. - 3 2 < m < - 1 3
B. 1 3 ≤ m < 3 2
C. 1 3 < m < 3 2
D. - 3 2 ≤ m < - 1 3
Tìm tất cả các giá trị của tham số m để phương trình cos 4 x = cos 2 3 x + m . sin 2 x có nghiệm x ∈ 0 , π 12
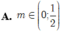
![]()
![]()
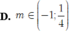
Tìm tất cả các giá trị của tham số m để phương trình log2 (|cos x|) – 2mlog(cos2 x) – m2 + 4 = 0 vô nghiệm?
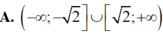
![]()

![]()
Đáp án C
Ta có : PT <=> log2 |cos x| – 2mlog|cos x| – m2 + 4 = 0
Đặt t = log|cos x|; t ∈ ( - ∞ ; 0 ]
Khi đó: t2 – 2mt – m2 + 4 = 0 (*)
PT đã cho vô nghiệm <= > (*) vô nghiệm hoặc có nghiệm dương.

Tìm tất cả các giá trị của tham số m để bất phương trình m( x - 1 ) < 3 - x có nghiệm?
A. m ≠ 1
B. m = 1
C. m ∈ R
D. m ≠ 3
Ta có: m(x - 1) < 3 – x
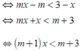
Bất phương trình tương đương là ( m + 1 )x < m + 3
Rõ ràng với m ≠ - 1 thì bất phương trình luôn có nghiệm
Với m = - 1 ta có bất phương trình có dạng: 0x < 2 luôn đúng với mọi x
Vậy bất phương trình có nghiệm với mọi m.
Chọn đáp án C.
ĐỀ THI HỌC KỲ I
Câu 1 : giải phương trình ln (3x2 - 2x +1) = ln ( 4x - 1)
Câu 2 : Tìm tập hợp các giá trị của tham số m để phương trình 3x + 3 = m \(\sqrt{9^x+1}\) có đúng 1 nghiệm
Câu 3 : Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số y = -x3 + 3mx + 1 có 2 điểm cực trị A , B sao cho tam giác OAB vuông tại O ( với O là gốc tọa độ )
Tập hợp tất cả các giá trị của tham số m để phương trình cos x = m+1 có đúng hai nghiệm phân biệt trên [0;3π/2] là: A. 4 B. 3 C.[-2;-1] D. (-2;1]
Vẽ vòng tròn lg
Pt có hai nghiệm pb trên \(\left[0;\dfrac{3\pi}{2}\right]\)\(\Leftrightarrow m+1\in(-1;0]\)
\(\Leftrightarrow m\in(-2;-1]\)
Ý D
Cho bất phương trình 3 + x + 1 - x ≤ m + 1 - x 2 - 2 x . Tìm tất cả các giá trị thực của tham số m để bất phương trình có nghiệm thực.
A. m ≥ 25 4
B. m ≥ 4
C. m ≥ 6
D. m ≥ 7
Cho bất phương trình 9 x + ( m - 1 ) . 3 x + 3 > 0 ( 1 ) . Tìm tất cả các giá trị của tham số m để bất phương trình (1) nghiệm đúng ∀ x > 1
A. m ≥ - 3 2
B. m > - 3 2
C. m > 3 + 2 2
D. m ≥ 3 + 2 2
Tìm tất cả các giá trị của tham số m để phương trình:\(\dfrac{2x-m}{x-1}+\dfrac{x+1}{x+2}=3\) có nghiệm
ĐKXĐ: \(x\ne1;x\ne-2\)\(\Rightarrow\left(2x-m\right)\left(x+2\right)+\left(x+1\right)\left(x-1\right)=3\left(x-1\right)\left(x+2\right)\Leftrightarrow2x^2+4x-mx-2m+x^2-1=3x^2+3x-6\Leftrightarrow3x^2+4x-mx-2m-3x^2-3x=-6\) \(\Leftrightarrow x-mx=2m-6\Leftrightarrow x\left(1-m\right)=2m-6\Leftrightarrow x=\dfrac{2m-6}{1-m}\)
\(\Rightarrow\) Để pt có nghiệm \(\Leftrightarrow m\ne1\) Vậy...
Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình x - 3 < 0 m - x < 1 vô nghiệm.
A. m < 4
B. m > 4
C. m ≤ 4
D. m ≥ 4
Chọn D
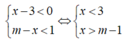
Hệ bất phương trình vô nghiệm khi và chỉ khi m - 1 ≥ 3 hay m ≥ 4
Cho phương trình m x 2 + ( m 2 - 3 ) x + m = 0 . Tìm tất cả các giá trị của tham số m để phương trình có hai nghiệm x 1 ; x 2 thỏa mãn x 1 + x 2 = 13 4 . Khi đó tổng bình phương các giá trị tìm được của tham số m bằng:
A. 265 16
B. 16
C. 9 16
D. 73 16
Phương trình có 2 nghiệm x 1 , x 2 thỏa mãn x 1 + x 2 = 13 4
⇔ a ≠ 0 Δ ≥ 0 − b a = 13 4 ⇔ m ≠ 0 m 2 − 3 3 − 4 m 2 ≥ 0 − m 2 − 3 m = 13 4
⇔ m ≠ 0 m 2 − 3 − 2 m m 2 − 3 + 2 m ≥ 0 4 m 2 + 13 m − 12 = 0
⇔ m ≠ 0 m + 1 m − 3 m − 1 m + 3 ≥ 0 m = 3 4 ; m = − 4
⇔ m ≠ 0 m ∈ − ∞ ; − 3 ∪ − 1 ; 1 ∪ 3 ; + ∞ m = 3 4 ; m = − 4 ⇔ m = 3 4 m = − 4
Vậy tổng bình phương các giá trị của m là: 265 16
Đáp án cần chọn là: A
hehe 1000000% dễễễễ