Tìm các cặp đường thẳng song song trong hình 13 và giải thích vì sao chúng song song.
Tìm các cặp đường thẳng song song trong hình 13 và giải thích vì sao chúng song song ?
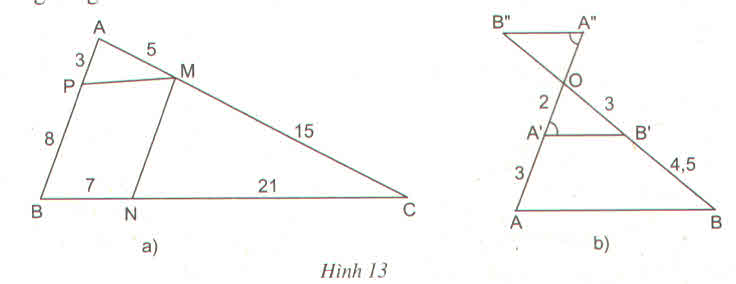
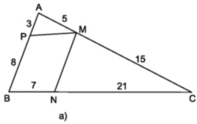
Trên hình 13a ta có:
= ; = = vì ≠ nên ≠ => PM và MC không song song.
Ta có => MN//AB
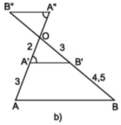
Trong hình 13b
Ta có: = ; = =
=>
1. Quan sát Hình 3.22 và giải thích vì sao AB // CD.
2. Tìm trên Hình 3.23 hai đường thẳng song song với nhau và giải thích vì sao chúng song song?
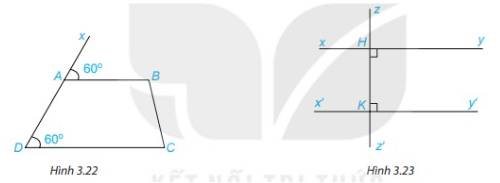
1. Vì \(\widehat {BAx} = \widehat {CDA}( = 60^\circ )\)
Mà 2 góc này ở vị trí đồng vị
\( \Rightarrow \) AB//CD (Dấu hiệu nhận biết hai đường thẳng song song)
2. Ta có: \(\widehat {zKy'} + \widehat {y'Kz'} = 180^\circ \) ( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow 90^\circ + \widehat {y'Kz'} = 180^\circ \\ \Rightarrow \widehat {y'Kz'} = 180^\circ - 90^\circ = 90^\circ \end{array}\)
Vì \(\widehat {yHz'} = \widehat {y'Kz'}\)
Mà 2 góc này ở vị trí đồng vị
\( \Rightarrow \) xy // x’y’ (Dấu hiệu nhận biết hai đường thẳng song song)
Chú ý:
2 đường thẳng cùng vuông góc với 1 đường thẳng thứ ba thì 2 đường thẳng đó song song.
Tìm cặp đường thẳng song song trong mỗi hình 53a, 53b, 53c, 53d và giải thích vì sao.


a) Vì \(\widehat {{A_1}} = \widehat {{B_1}}( = 124^\circ )\). Mà 2 góc này ở vị trí so le trong nên z // t
b) Vì \(\widehat {{D_1}}= \widehat {{C_1}} (= 90^\circ) \)
Mà 2 góc này ở vị trí đồng vị nên m // n
c) Vì \(\widehat {{E_1}} + \widehat {{E_2}} = 180^\circ \) ( 2 góc kề bù) nên \(110^\circ + \widehat {{E_2}} = 180^\circ \Rightarrow \widehat {{E_2}} = 180^\circ - 110^\circ = 70^\circ \)
Vì \(\widehat {{E_2}} = \widehat {{G_1}}( = 70^\circ )\). Mà 2 góc này ở vị trí so le trong nên x // y
d) Vì \(\widehat {{K_1}} + \widehat {{K_2}} = 180^\circ \) ( 2 góc kề bù) nên \(\widehat {{K_1}} + 56^\circ = 180^\circ \Rightarrow \widehat {{K_1}} = 180^\circ - 56^\circ = 124^\circ \)
Vì \(\widehat {{H_1}} = \widehat {{K_1}}( = 124^\circ )\). Mà 2 góc này ở vị trí so le trong nên u // v
Tìm các cặp đường thẳng song song trong Hình 5 và giải thích.
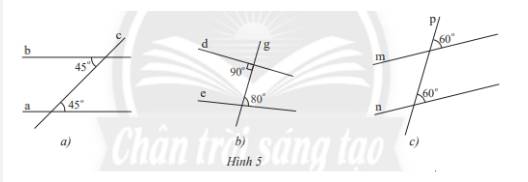
Xét hình a: a // b vì đường thẳng c cắt 2 đường thẳng a, b và tạo thành một cặp góc so le trong bằng nhau
Xét hình b: không có cặp đường thẳng nào song song vì đường thẳng g cắt 2 đường thẳng d, e và không tạo thành một cặp góc so le trong bằng nhau ( 90 \(^\circ \) 80 \(^\circ \))
Xét hình c: m // n vì đường thẳng p cắt 2 đường thẳng m, n và tạo thành một cặp góc đồng vị bằng nhau
chỉ ra các cặp đường thẳng song song trong mỗi hình vẽ 8 ,9 ,10, 11 và giải thích tại sao
*) Hình 8
Ta có:
∠C + ∠MNC = 65⁰ + 115⁰
= 180⁰
Mà ∠C và ∠MNC là hai góc trong cùng phía
⇒ MN // BC
*) Hình 9
Ta có:
∠C + ∠NMC = 30⁰ + 150⁰
= 180⁰
Mà ∠C và ∠NMC là hai góc trong cùng phía
⇒ MN // BC
*) Hình 10
Ta có:
∠ANx + ∠ANM = 180⁰ (kề bù)
⇒ ∠ANM = 180⁰ - ∠ANx
= 180⁰ - 110⁰
= 70⁰
⇒ ∠ANM = ∠NBC = 70⁰
Mà ∠ANM và ∠NBC là hai góc đồng vị
⇒ MN // BC
*) Hình 11
Ta có:
∠x'Az + ∠x'AB = 180⁰ (kề bù)
⇒ ∠x'AB = 180⁰ - ∠x'Az
= 110⁰ - 130⁰
= 50⁰
⇒ ∠x'AB = ∠y'Bz' = 50⁰
Mà ∠x'AB và ∠x'Az' là hai góc đồng vị
⇒ xx' // yy'
Bài 8:
Ta có: \(a//b\Rightarrow\widehat{D_1}=\widehat{DAB}\) (đồng vị)
Mà: \(\widehat{DAB}=90^o\)
\(\Rightarrow\widehat{D_1}=90^o\)
Và: \(a//b\Rightarrow\widehat{DCB}=\widehat{B_1}\) (so le trong)
Mà: \(\widehat{DCB}=130^o\)
\(\Rightarrow\widehat{B_1}=130^o\)
Hình 82 vẽ một phòng ở. Quan sát hình và giải thích vì sao:
a) Đường thẳng b song song với mp(P)?
b) Đường thẳng p song song với sàn nhà?
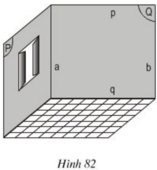
a) Ta có b không thuộc mặt phẳng (P) và b // a, a nằm trong (P). Nên b// (P).
b) Ta có p không thuộc sàn nhà và đường thẳng p song song với đường thẳng q trong sàn nhà nên p song song với sàn nhà.
Hình 82 vẽ một phòng ở. Quan sát hình và giải thích vì sao:
a) Đường thẳng b song song với mp(P)?
b) Đường thẳng p song song với sàn nhà?
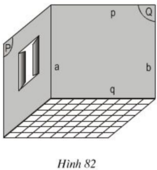
a) Ta có b không thuộc mặt phẳng (P) và b // a, a nằm trong (P). Nên b// (P).
b) Ta có p không thuộc sàn nhà và đường thẳng p song song với đường thẳng q trong sàn nhà nên p song song với sàn nhà.
Bai 2:Cho các hình vẽ dưới đây
a) Kể tên các cặp góc so le trong, đồng vị, trong cung phía.
b) Tính \(F_1;F_2;F_3;F_4\)
c) Hai đường thẳng a, b có song song với nhau không? Vì sao? ( nếu có giải thích bằng 2 cách)
\(a,\)So le trong: \(E_1 và F_2;E_2 và F_1\)
Đồng vị: \(E_1 và F_4;E_2 và F_3;E_3 và F_2;E_4 và F_1\)
Trong cùng phía: \(E_1 và F_1;E_2 và F_2\)
\(b,\widehat{F_1}=\widehat{F_3}=120^0\left(đối.đỉnh\right)\\ \widehat{F_2}+\widehat{F_3}=180^0\left(kề.bù\right)\Rightarrow\widehat{F_2}=180^0-120^0=60^0\\ \widehat{F_2}=\widehat{F_4}-60^0\left(đối.đỉnh\right)\)
\(c,C_1:\widehat{F_2}=\widehat{E_3}\left(=60^0\right)\)
Mà 2 góc này ở vị trí đồng vị nên \(a//b\)
\(C_2:\)\(\widehat{E_1}=\widehat{E_3}=60^0\left(đối.đỉnh\right)\Rightarrow\widehat{E_1}=\widehat{F_2}\left(=60^0\right)\)
Mà 2 góc này ở vị trí so le trong nên \(a//b\)
a. Các cặp góc:
- So le trong là: \(\widehat{E_1}\) và \(\widehat{F_2};\widehat{E_2}\) và \(\widehat{F_1}\)
- Đồng vị là: \(\widehat{E_4},\widehat{F_1};\widehat{E_3},\widehat{F_2};\widehat{E_2},\widehat{F_3};\widehat{E_1},\widehat{F_4}\)
- Trong cùng phía là: \(\widehat{E_1},\widehat{F_1};\widehat{E_2},\widehat{F_2}\)
b. Ta có: \(\widehat{F_1}=\widehat{F_3}=120^o\) (đối đỉnh)
\(\widehat{F_2}=180^o-\widehat{F_1}=180^o-120^o=60^o\)
\(\widehat{F_3}=120^o\)
\(\widehat{F_4}=\widehat{F_2}=60^o\) (đối đỉnh)
c.
C1: Ta có: \(\widehat{E_1}=\widehat{E_3}=60^o\) (đối đỉnh)
Ta thấy: \(\widehat{E_1}=\widehat{F_2}=60^o\)
=> a//b (so le trong)
C2: Ta có: \(\widehat{E_2}=180^o-\widehat{E_3}=180^o-60^o=120^o\)
Ta thấy: \(\widehat{E_2}=\widehat{F_1}=120^o\)
=> a//b (so le trong)
a) Trong cùng phía:
-E1 và F2
-E2 và F4
Đồng vị:
- E1 và F4
- E2 và F3
- E4 và F1
- E3 và F2
Trong cùng phía:
- E1 và F1
E2 và F2
b) Vì E3 và F2 là hai góc đồng vị
-> E3 = F2 = 60O
Vì F1 và F2 là hai góc kề bù
-> F1 + F2 = 180o
Thay số: F1 + 60O = 180O
-> F1 = 180O – 60O = 120O
Vì F3 và F4 là hai góc kề bù
-> F3 + F4 = 180O
Thay số: 120o + F4 = 180O
-> F4 = 180O – 120O = 60O
c) Vì E3 và F3 là hai góc ngoài cùng phía
-> a//b
Vậy a//b
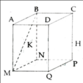
Cho hình hộp chữ nhật ABCD.A'BC'D' như hình vẽ.
a) Cặp đường thẳng BB' và A'D'; CD và B'C' có cắt nhau không?
b) Đường thẳng AB có song song với C'D' không? Vì sao?
c) Nêu vị trí tương đối của (ABB'A') với (BDD'B')và (CDD'C')? Giải thích ?
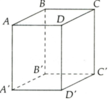
a) BB' và A'D' chéo nhau, CD và B'C' chéo nhau.
b) AB song song với CD (hoặc A'B')
c) (ABB'A') cắt (BDD'B') theo giao tuyến BB', (ABB'A')// (CDD'C') vì AB và AA' song song với (CDD'C').