Cho hai đa thức P ( x ) = 2 x 2 + 5 x - 1 , Q ( x ) = - 2 x 2 - 4 x + 3 . Nghiệm của P ( x ) + Q ( x ) là:
A. x = -1
B. x = 1
C. x = -2
D. x = 2
1) Cho hai đa thức: P=(x-1)(x+2)(x+4)(x+7)+2070 và Q=x2+6x+2
Tìm số dư của phép chia đa thức P cho đa thức Q
2) Cho biểu thức A=(x^2+6x+5)/(x^2+2x-15). Tìm số nguyên x để biểu thức A đạt giá trị nguyên
cho đa thức f(x) = x^2 - 4x - 5 Chứng tỏ rằng x= -1 ; x = 5 là hai nghiệm của đa thức đó
f(-1)=1+4-5=0
f(5)=25-20-5=0
Do đó: x=-1; x=5 là các nghiệm của f(x)
Ta có \(f\left(-1\right)=1+4-5=0\)
Vậy x = -1 là nghiệm đa thức trên
\(f\left(5\right)=25-20-5=0\)
Vậy x = 5 là nghiệm đa thức trên
bài 1: cho hai đa thức f(x) = -x + 2x^2 - 1/2 + 3x^5 + 5
g(x) = 3-x^5 + 1/3x^3 + 3x - 2x^5 - 2x^2 - 1/3x^3
a) thu gọn và sắp xếp hai đa thức f(x) và g(x) theo lũy thừa giảm dần của biến
b) tính f(x) + g(x)
c) tìm nghiệm của đa thức h(x) = f(x) + g(x)
Cho đa thức \(f\left(x\right)=x^2-4x-5\) Chứng tỏ rằng \(x=-1;x=5\) là hai nghiệm của đa thức đó.
Đặt \(f\left(x\right)=0\)
\(\Leftrightarrow x^2-4x-5=0\)
\(\Leftrightarrow x^2+x-5x-5=0\)
\(\Leftrightarrow x\left(x+1\right)-5\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x-5\right)=0\)
\(\rightarrow\left[{}\begin{matrix}x+1=0\\x-5=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=5\end{matrix}\right.\)
--> hai nghiệm \(x=-1;x=5\) là hai nghiệm của đa thức \(f\left(x\right)\)
đặt f(x) = 0
\(\Leftrightarrow x^2-4x-5=0\\ \Leftrightarrow x^2+x-5x-5=0\\ \Leftrightarrow x\left(x+1\right)-5\left(x+1\right)=0\\ \Leftrightarrow\left(x+1\right)\left(x-5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-5=0\\x+1=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
Vậy x = 5 và x = -1 là 2 nghiệm của f(x)
Thay x = -1 vào đa thức f(x) có
f(x) = x2 - 4x - 5
f(-1) = (-1)2 -4.(-1) - 5
f(-1) = 0
Vậy x = -1 và nghiệm của đa thức f(x)
Thay x = 5 vào đa thức f(x) có
f(x) = x2 - 4x - 5
f(5) = =52 -4.5 - 5
f(5) = 0
Vậy x = 5 và nghiệm của đa thức f(x)
Bài 1 . cho hai đa thức: P(x) = 4x4 - 2x3 - 7x2 + 2x + 1/3 và Q(x) = x4 + 3x3 - 6x2 - x - 1/4
a. Tính P(x) + Q(x);
b. Tính P(x) - Q(x).
Bài 2. cho đa thức: M(x) = x2 - 2x3 + x + 5 và N(x) = 2x3 - x - 6
a. Tính M(2)
b. Tìm đa thức A(x) sao cho A(x) = M(x) + N(x); A(x), tính B(x) = M(x) - N(x)
c. Tìm nghiệm của đa thức A(x)
Bài 3. Tìm nghiệm của các đa thức sau:
a. 2x - 8 b. 2x + 7 c. 4 - x2 d. 4x2 - 9
e. 2x2 - 6 f. x(x - 1) g. x + 2x h. x( x + 2 )
Bài 4. cho hai đa thức: f(x) = 2x4 + 3x2 - x + 1 - x2 - x4 - 6x3
g(x) = 10x3 + 3 - x4 - 4x3 + 4x - 2x2
a. Thu gọn đa thức: f(x), g(x) và sắp xếp các hạng tử của mỗi đa thức theo lũy thừa giảm dần của biến.
b. Tính h(x) = f(x) + g(x); K(x) = f(x) - g(x)
c. Tìm nghiệm của đa thức h(x)
Bài 5. Tìm nghiệm của các đa thức:
a. 9 - 3x b. -3x + 4 c. x2 - 9 d. 9x2 - 4
e. x2 - 2 f. x( x - 2 ) g. x2 - 2x h. x(x2 + 1 )
Tách ra, dài quá mn đọc là mất hứng làm đó.
(Nghỉ dịch từ ngày 28/2/2022)
Bài 1:
a) Cho hai đa thức: M = 2x2 – 2xy – 3y2 + 1; N = x2 – 2xy + 3y2 – 1
Tính M + N; M – N.
b) Cho hai đa thức: P(x) = x3 – 6x + 2; Q(x) = 2x2 - 4x3 + x - 5
+ Tính P(x) + Q(x)
+ Tính P(x) - Q(x)
Bài 2: Tìm x biết:
a) (x - 8 )( x3+ 8) = 0; b) (4x - 3) – ( x + 5) = 3(10 - x)
Bài 3: Cho đa thức: P(x) = 5x3 + 2x4 – x2 + 3x2 – x3 – 2x4 + 1 – 4x3.
a) Thu gọn và xắp sếp các hạng tử của đa thức trên theo lũy thừa giảm của biến.
b) Tính P(1) và P(–1).
Bài 4: Tính nhanh (nếu có thể):
Bài 5: Cho tam giác ABC có AB = AC = 5cm, BC = 6cm. Đường trung tuyến AM xuất phát từ đỉnh A của tam giác ABC.
a) Chứng minh ΔAMB = ΔAMC và AM là tia phân giác của góc A.
b) Chứng minh AM vuông góc với BC.
c) Tính độ dài các đoạn thẳng BM và AM.
d) Từ M vẽ ME AB (E thuộc AB) và MF AC (F thuộc AC). Tam giác MEF là tam giác gì? Vì sao?
Bài 6: Cho ΔABC cân có AB = AC = 5cm, BC = 8cm. Kẻ AH vuông góc với BC.
a) Chứng minh: HB = HC.
b) Tính độ dài AH.
c) Kẻ HD vuông góc với AB (D∈AB), kẻ HE vuông góc với AC (E∈AC).
Chứng minh ΔHDE cân.
d) So sánh HD và HC.
Bài 2:
a: \(\left(x-8\right)\left(x^3+8\right)=0\)
=>\(\left[{}\begin{matrix}x-8=0\\x^3+8=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=8\\x^3=-8\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-2\end{matrix}\right.\)
b: \(\left(4x-3\right)-\left(x+5\right)=3\left(10-x\right)\)
=>\(4x-3-x-5=30-3x\)
=>3x-8=30-3x
=>6x=38
=>\(x=\dfrac{38}{6}=\dfrac{19}{3}\)
Bài 6:
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>HB=HC
b: Ta có: HB=HC
H nằm giữa B và C
Do đó: H là trung điểm của BC
=>\(HB=HC=\dfrac{8}{2}=4\left(cm\right)\)
ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AH^2=5^2-4^2=9\)
=>\(AH=\sqrt{9}=3\left(cm\right)\)
c: Ta có: ΔAHB=ΔAHC
=>\(\widehat{BAH}=\widehat{CAH}\)
Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
=>HD=HE
=>ΔHDE cân tại H
d: Ta có: HD=HE
HE<HC(ΔHEC vuông tại E)
Do đó:HD<HC
cho hai đa thức:
f(x)=-x+2x^2-1/2+3x^5+5 và g(x)=3-x^5+1/3x^3+3x-2x^5-2x^2-1/3x^3
a)thu gọn và sắp xếp 2 đa thức trên theo lũy thừa giảm dần của biến
b) Tính f(x)+g(x)
c) Tìm ngiệm của đa thức
h(x)=f(x)+g(x)
Cho hai đa thức:
P(x)=(x+1)(x+3)(x+5)(x+7)+a và Q(x)=x2+8x+9
Tìm giá trị của a để đa thức P(x) chia hết cho đa thức Q(x)
a) Cho hai đa thức: M = 2x2 – 2xy – 3y2 + 1; N = x2 – 2xy + 3y2 – 1
Tính M + N; M – N.
b) Cho hai đa thức: P(x) = x3 – 6x + 2; Q(x) = 2x2 - 4x3 + x - 5
+ Tính P(x) + Q(x)
+ Tính P(x) - Q(x)
a, \(M+N=2x^2+x^2-2xy-2xy-3y^2+3y^2+1-1=3x^2-4xy\)
\(M-N=2x^2-x^2-2xy+2xy-3y^2-3y^2+1+1=x^2-6y^2+2\)
b, \(P\left(x\right)+Q\left(x\right)=x^3-4x^3+2x^2-6x+x+2-5=-3x^3+2x^2-5x-3\)
\(P\left(x\right)-Q\left(x\right)=x^3+4x^3-2x^2-6x-x+2+5=5x^3-2x^2-7x+7\)
Cho hai đa thức
\(P(x) = 5{x^2} + 4 + 2x\) và \(Q(x) = 8x + {x^2} + 1\).
a) Sắp xếp các đa thức P(x), Q(x) theo số mũ giảm dần của biến.
b) Tìm đơn thức thích hợp trong dạng thu gọn của P(x) và Q(x) cho ? ở bảng sau rồi cộng hai đơn thức theo từng cột và thể hiện kết quả ở dòng cuối cùng của mỗi cột:
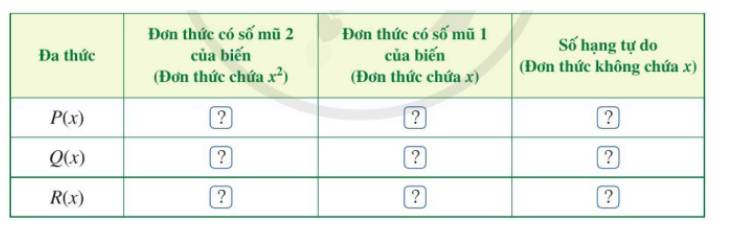
c) Dựa vào kết quả cộng hai đơn thức theo từng cột, xác định đơn thức R(x).
a) Sắp xếp đa thức (một biến) theo số mũ giảm dần của biến là sắp xếp các đơn thức trong dạng thu gọn của đa thức đó theo số mũ giảm dần của biến.
b) Quan sát bảng để đưa ra các đơn thức thích hợp phù hợp với biến có số mũ tương ứng.
c) Xác định đơn thức R(x) dựa vào kết quả phần b).
Lời giải chi tiết:
a) \(P(x) = 5{x^2} + 4 + 2x = 5{x^2} + 2x + 4\); \(Q(x) = 8x + {x^2} + 1 = {x^2} + 8x + 1\).
b)
Đa thức | Đơn thức có số mũ 2 của biến (Đơn thức chứa \({x^2}\)) | Đơn thức có số mũ 1 của biến (Đơn thức chứa x) | Số hạng tự do (Đơn thức không chứa x) |
P(x) | \(5{x^2}\) | 2x | 4 |
Q(x) | \({x^2}\) | 8x | 1 |
R(x) | \(6{x^2}\) | 10x | 5 |
c) Vậy \(R(x) = 6{x^2} + 10x + 5\).