Cho a = log 2 m và A = log m 8 m với 0 < m ≠ 1 . Chọn khẳng định đúng
A. A = (3 - a).a
B. A = (3 + a).a
C. A = 3 - a a
D. A = 3 + a a
Hoạt động 3
Cho \(m = {2^7};\,n = {2^3}\)
a) Tính \({\log _2}\left( {mn} \right);{\log _2}m + {\log _2}n\) và so sánh các kết quả đó
b) Tính \({\log _2}\left( {\frac{m}{n}} \right);{\log _2}m - {\log _2}n\) và so sánh các kết quả đó
a: \(log_2\left(mn\right)=log_2\left(2^7\cdot2^3\right)=7+3=10\)
\(log_2m+log_2n=log_22^7+log_22^3=7+3=10\)
=>\(log_2\left(mn\right)=log_2m+log_2n\)
b: \(log_2\left(\dfrac{m}{n}\right)=log_2\left(\dfrac{2^7}{2^3}\right)=7-3=4\)
\(log_2m-log_2n=log_22^7-log_22^3=7-3=4\)
=>\(log_2\left(\dfrac{m}{n}\right)=log_2m-log_2n\)
a) \(\log_2\left(mn\right)=\log_2\left(2^7.2^3\right)=\log_22^{7+3}=\log_22^{10}=10.\log_22=10.1=10\)
\(\log_2m+\log_2n=\log_22^7+\log_22^3=7\log_22+3\log_22=7.1+3.1=7+3=10\)
b) \(\log_2\left(\dfrac{m}{n}\right)=\log_2\dfrac{2^7}{2^3}=\log_22^4=4.\log_22=4.1=4\)
\(\log_2m-\log_2n=\log_22^7-\log_22^3=7.\log_22-3\log_22=7.1-3.1=4\)
Cho M = 25, N = 23. Tính và so sánh:
a) \({\log _2}\left( {MN} \right)\) và \({\log _2}M + {\log _2}N;\)
b) \({\log _2}\left( {\frac{M}{N}} \right)\) và \({\log _2}M - {\log _2}N.\)
a: \(log_2\left(M\cdot N\right)=log_2\left(2^5\cdot2^3\right)=log_2\left(2^8\right)=8\)
\(log_2M+log_2N=log_22^5+log_22^3=5+3=8\)
=>\(log_2\left(MN\right)=log_2M+log_2N\)
b: \(log_2\left(\dfrac{M}{N}\right)=log_2\left(\dfrac{2^5}{2^3}\right)=log_2\left(2^2\right)=2\)
\(log_2M-log_2N=log_22^5-log_22^3=5-3=2\)
=>\(log_2\left(\dfrac{M}{N}\right)=log_2M-log_2N\)
Đặt m = log 2 và n = log 7. Hãy biểu diễn log 6125 7 theo m và n.
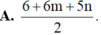
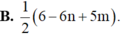
![]()
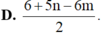
Đáp án D.
Ta có
log 6125 7 = log 6125 + log 7 = log 7 2 . 125 + 1 2 log 7
= 5 2 log 7 + log 5 3 = 5 2 n + 3 log 5 = 5 2 n + 3 1 - log 2
= 5 2 n + 3 - 3 m .
Giả sử đã cho \({\log _a}M\) và ta muốn tính \({\log _b}M.\) Để tìm mối liên hệ giữa \({\log _a}M\) và \({\log _b}M,\) hãy thực hiện các yêu cầu sau:
a) Đặt \(y = {\log _a}M,\) tính M theo y;
b) Lấy loogarit theo cơ số b cả hai vế của kết quả nhận được trong câu a, từ đó suy ra công thức mới để tính y.
a) \(y = {\log _a}M \Leftrightarrow M = {a^y}\)
b) Lấy loogarit theo cơ số b cả hai vế của \(M = {a^y}\) ta được
\({\log _b}M = {\log _b}{a^y} \Leftrightarrow {\log _b}M = y{\log _b}a \Leftrightarrow y = \frac{{{{\log }_b}M}}{{{{\log }_b}a}}\)
1. cho a=log3 2 và b=log3 5. tính các logarit sau theo a, b; A=log3 80, B=log3 37,5
2. cho log10 3=a, log5=b. tính C=log30 8 theo a, b
3. cho log27 5=a, log8 7=b, log2 3=c. tính D log6 35 theo a, b, c
Bài 1:
\(A=\log_380=\log_3(2^4.5)=\log_3(2^4)+\log_3(5)\)
\(=4\log_32+\log_35=4a+b\)
\(B=\log_3(37,5)=\log_3(2^{-1}.75)=\log_3(2^{-1}.3.5^2)\)
\(=\log_3(2^{-1})+\log_33+\log_3(5^2)=-\log_32+1+2\log_35\)
\(=-a+1+2b\)
Bài 2:
\(\log_{30}8=\frac{\log 8}{\log 30}=\frac{\log (2^3)}{\log (10.3)}=\frac{3\log2}{\log 10+\log 3}\)
\(=\frac{3\log (\frac{10}{5})}{1+\log 3}=\frac{3(\log 10-\log 5)}{1+\log 3}=\frac{3(1-b)}{1+a}\)
Bài 3:
\(\log_{27}5=a; \log_87=b; \log_23=c\)
\(\Leftrightarrow \frac{\ln 5}{\ln 27}=a; \frac{\ln 7}{\ln 8}=b; \frac{\ln 3}{\ln 2}=c\)
\(\Leftrightarrow \frac{\ln 5}{\ln (3^3)}=a; \frac{\ln 7}{\ln (2^3)}=b; \ln 3=c\ln 2\)
\(\Leftrightarrow \frac{\ln 5}{3\ln 3}=a; \frac{\ln 7}{3\ln 2}=b; \ln 3=c\ln 2\)
\(\Rightarrow \frac{\ln 5}{3c\ln 2}=a; \frac{\ln 7}{3\ln 2}=b\)
\(\Rightarrow \ln 35=\ln 5+\ln 7=3ac\ln 2+3b\ln 2\)
Do đó:
\(D=\log_6 35=\frac{\ln 35}{\ln 6}=\frac{\ln 35}{\ln 2+\ln 3}=\frac{\ln 35}{\ln 2+c\ln 2}=\frac{3ac\ln 2+3b\ln 2}{\ln 2+c\ln 2}\)
\(=\frac{3ac+3b}{1+c}\)
1) Cho a,b là các số thực dương khác 1 và thoả mãn ab khác 1. Rút gọn biểu thức sau: P=(logab + logba + 2)(logab - logabb).logba - 1
Cho a,bc>1.Biết rằng biểu thức P= loga(bc) +logb(ac)+4logc(ab) đạt giá trị nhỏ nhất bằng m khi logbc=n. Tính giá trị m+n
Lời giải:
Đặt \(\left\{\begin{matrix} \log_ab=x\\ \log_bc=y\\ \log_ca=z\end{matrix}\right.\Rightarrow \left\{\begin{matrix} \log_ba=\frac{1}{x}\\ \log_cb=\frac{1}{y}\\ \log_ac=\frac{1}{z}\end{matrix}\right. \). và \(xyz=1\)
Do \(a,b,c>1\Rightarrow x,y,z>0\)
Ta có:
\(P=\log_a(bc)+\log_b(ac)+4\log_c(ab)\)
\(=\log_ab+\log_ac+\log_ba+\log_bc+4\log_ca+4\log_cb\)
\(=x+\frac{1}{z}+\frac{1}{x}+y+4z+\frac{4}{y}\)
Áp dụng BĐT Cô-si cho các số dương:
\(\left\{\begin{matrix} x+\frac{1}{x}\geq 2\sqrt{1}=2\\ y+\frac{4}{y}\geq 2\sqrt{4}=4\\ \frac{1}{z}+4z\geq 2\sqrt{4}=4\end{matrix}\right.\) \(\Rightarrow P\geq 2+4+4=10\)
\(\Rightarrow m=10\)
Dấu bằng xảy ra khi \(\left\{\begin{matrix} x=\frac{1}{x}\rightarrow x=1\\ y=\frac{4}{y}\rightarrow y=2\\ \frac{1}{z}=4z\rightarrow z=\frac{1}{2}\end{matrix}\right.\) (thỏa mãn)
Suy ra \(n=\log_bc=y=2\)
\(\Rightarrow m+n=12\)
Tính giá trị của các biểu thức sau:
a) \(A = {\log _2}3.{\log _3}4.{\log _4}5.{\log _5}6.{\log _6}7.{\log _7}8;\)
b) \(B = {\log _2}2.{\log _2}4...{\log _2}{2^n}.\)
\(a,A=log_23\cdot log_34\cdot log_45\cdot log_56\cdot log_67\cdot log_78\\ =log_28\\ =log_22^3\\ =3\\ b,B=log_22\cdot log_24...log_22^n\\ =log_22\cdot log_22^2...log_22^n\\ =1\cdot2\cdot...\cdot n\\ =n!\)
Cho các số thực dương \(a,M,N\) với \(a \ne 1\). Bạn Quân đã vẽ sơ đồ và tìm ra công thức biến đổi biểu thức \({\log _a}\left( {MN} \right)\) như sau:
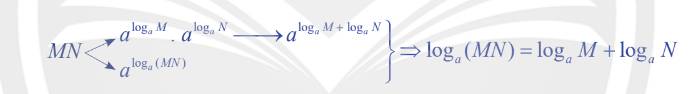
a) Giải thích cách làm của bạn Quân.
b) Vẽ sơ đồ tương tự để tìm công thức biến đổi cho \({\log _a}\frac{M}{N}\) và \({\log _a}{M^\alpha }\left( {\alpha \in \mathbb{R}} \right)\).
Tham khảo:
a) Ta có: \(M = {a^{{{\log }_a}M}},N = {a^{{{\log }_a}N}} \Rightarrow MN = {a^{{{\log }_a}M}}.{a^{{{\log }_a}N}} = {a^{{{\log }_a}M + {{\log }_a}N}}\)
Mặt khác: \(MN = {a^{{{\log }_a}\left( {MN} \right)}}\)
Vậy \({a^{{{\log }_a}M + {{\log }_a}N}} = {a^{{{\log }_a}\left( {MN} \right)}} \Leftrightarrow {\log _a}M + {\log _a}N = {\log _a}\left( {MN} \right)\)
b)
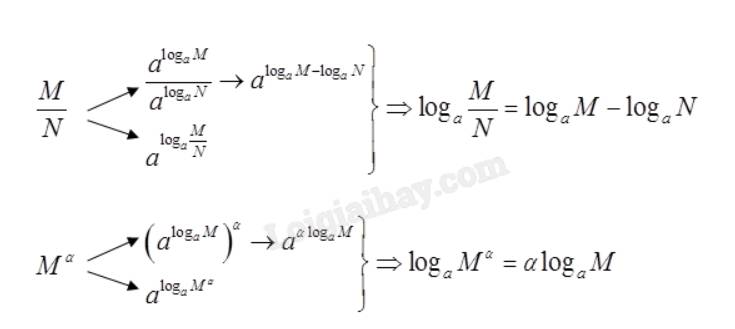
Cho hai số thực dương a, b với \(a \ne 1\). Khẳng định nào sau đây là đúng?
A. \({\log _a}\left( {{a^3}{b^2}} \right) = 3 + {\log _a}b\).
B. \({\log _a}\left( {{a^3}{b^2}} \right) = 3 + 2{\log _a}b\).
C. \({\log _a}\left( {{a^3}{b^2}} \right) = \frac{3}{2} + {\log _a}b\).
D. \({\log _a}\left( {{a^3}{b^2}} \right) = \frac{1}{3} + \frac{1}{2}{\log _a}b\).
\(log_a\left(a^3b^2\right)=log_aa^3+log_ab^2=3+2\cdot log_ab\)
=>B