Số điểm biểu diễn nghiệm của phương trình 8 cot 2 x sin 6 x + cos 6 x = 1 2 sin 4 x trên đường tròn lượng giác là
A. 2
B. 4
C. 6
D. 0
Số điểm biểu diễn cung lượng giác có số đo là nghiệm của phương trình c o t x = tan x + 2 . cos 4 x sin 2 x trên đường tròn lượng giác là
A. 2
B. 3
C. 6
D. 4
1) nghiệm dương nhỏ nhất của phương trình \(cot\left(x-\dfrac{\pi}{6}\right)=\sqrt{3}\) là
2) phương trình \(sin\left(\dfrac{2x}{3}+\dfrac{\pi}{3}\right)=0\) có nghiệm là
3) họ nghiệm của phương trình \(cot\)(2x - 30 độ) = \(\sqrt{3}\) là
Tìm số họ nghiệm của phương trình cot (sin x) = 1
A. 1.
B. 2.
C. 3.
D. 4.
Nghiệm của phương trình 2 . sin x - 2 = 0 được biểu diễn trên đường tròn lượng giác ở hình bên là những điểm nào?
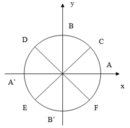
A. Điểm C, điểm E
B. Điểm F, điểm E
C. Điểm C, điểm D
D. Điểm C, điểm F
Giải phương trình sau:
a) $\tan ^2x+4\cos ^2x+7=4\tan x+8\cot x$
b) $6\sin ^2x+2\cos ^2x-2\sqrt{3}\sin 2x=14\sin \left(x-\frac{\pi }{6}\right)$
Giải phương trình
\(\sin x+2\cos x+2\tan x+4\cot x+6=0\)
a) giải phương trình: 8x-3=5x+12
b) giải bất phương trình sau và biểu diễn tập hợp nghiệm trên trục số: \(\dfrac{8-11x}{4}\)< 13
c) Chứng minh rằng: (\(\dfrac{x}{x^2-36}\)- \(\dfrac{x-6}{x^2+6x}\)): \(\dfrac{2x-6}{x^2+6x}\)+ \(\dfrac{x}{6-x}\)= 1
a:=>3x=15
=>x=5
b: =>8-11x<52
=>-11x<44
=>x>-4
c: \(VT=\left(\dfrac{x^2-\left(x-6\right)^2}{x\left(x+6\right)\left(x-6\right)}\right)\cdot\dfrac{x\left(x+6\right)}{2x-6}+\dfrac{x}{6-x}\)
\(=\dfrac{12x-36}{2x-6}\cdot\dfrac{1}{x-6}-\dfrac{x}{x-6}=\dfrac{6}{x-6}-\dfrac{x}{x-6}=-1\)
Đề thi môn toán 8 học kì 2
Câu 1 Giải các phương trình sau:
a) x-2=0, b) (x+5)(2x-7)=0. =c) . 5x/x+2 =4
Câu 2. a) Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số: a )2x-6>_(hoặc bằng)=0.
b) Cho a<b. Chứng minh
: -3a+7> -3b+7
Câu 3 (1,0 điểm). Giải bài toán bằng cách lập phương trình:
Một người đi ôtô từ huyện Cao Lãnh đến huyện Thanh Bình với vận tốc 40 km/h. Sau khi đi đến huyện Thanh Bình người đó giải quyết công việc hết 30 phút .rồi quay về huyện Cao Lãnh với vận tốc 50 km/h. Biết thời gian cả đi và về hết 2 giờ 18 phút (kể cả thời gian giải quyết công việc). Tính quãngđường từ huyện Cao Lãnh đến huyện Thanh Bình.
Câu 4 (1,0 điểm). Một container chứa hàng có kích thước như sau: dài 6m, rộng 2,4m; cao 2,6m. Tínhthể tích của thùng container.
Câu 5 (3,0 điểm). Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm. Kẻ AH vuông góc với BC tại H
a) Chứng minh: tamgiácHBA đồng dạng với tamgiácABC.
b) Chứng minh: AB2 =BH.BC
c) Tính độ dài cạnh BC, BH.
Phân giác của góc ACB cắt AH tại E và cắt AB tại D. Tính tỉ số diện tích của tam giác ACD và tam giácHCE.
Giúp mình với mn ơii .mai mình nộp r
GIUP VOI MOI NGUOI OI .CUU EM VOIIIIII !!!!!!!!!!
câu 1
a) 5x(x-2)=0 =>\(\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
b)(x+5)(2x-7)=0 =>\(\left[{}\begin{matrix}x+5=0\\2x-7=0\end{matrix}\right.\)=>\(\left[{}\begin{matrix}x=-5\\x=\dfrac{7}{2}\end{matrix}\right.\)
Phương trình: \(\dfrac{Sin^42x+Cos^42x}{Tan\left(\dfrac{\pi}{4}-x\right)Tan\left(\dfrac{\pi}{4}+x\right)}=Cos^4x\) có bao nhiêu điểm biểu diễn nghiệm trên đường tròn lượng giác
\(\dfrac{sin^42x+cos^42x}{tan\left(\dfrac{\pi}{4}-x\right)tan\left(\dfrac{\pi}{4}+x\right)}=cos^4x\)
\(\Leftrightarrow\dfrac{sin^42x+cos^42x}{cot\left(\dfrac{\pi}{4}+x\right)tan\left(\dfrac{\pi}{4}+x\right)}=cos^4x\)
\(\Leftrightarrow sin^42x+cos^42x=cos^4x\)
Giờ hạ bậc nữa là xong rồi. Làm nốt
Hình như đề bạn bị lỗi, thấy chỗ nào cũng ghi là \(cos^44x\).
ĐK: \(x\ne\dfrac{3\pi}{4}+k\pi;x\ne\dfrac{\pi}{4}+k\pi\)
\(\dfrac{sin^42x+cos^42x}{tan\left(\dfrac{\pi}{4}-x\right).tan\left(\dfrac{\pi}{4}+x\right)}=cos^44x\)
\(\Leftrightarrow\dfrac{sin^42x+cos^42x}{\dfrac{sin\left(\dfrac{\pi}{4}-x\right)}{cos\left(\dfrac{\pi}{4}-x\right)}.\dfrac{sin\left(\dfrac{\pi}{4}+x\right)}{cos\left(\dfrac{\pi}{4}+x\right)}}=cos^44x\)
\(\Leftrightarrow\dfrac{sin^42x+cos^42x}{\dfrac{cosx-sinx}{cosx+sinx}.\dfrac{cosx+sinx}{cosx-sinx}}=cos^44x\)
\(\Leftrightarrow sin^42x+cos^42x=cos^44x\)
\(\Leftrightarrow1-\dfrac{1}{2}sin^24x=cos^44x\)
\(\Leftrightarrow cos^44x-\dfrac{1}{2}cos^24x-\dfrac{1}{2}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos^24x=1\\cos^24x=-\dfrac{1}{2}\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{1}{2}cos8x=\dfrac{1}{2}\)
\(\Leftrightarrow cos8x=1\)
\(\Leftrightarrow x=\dfrac{k\pi}{4}\)
Đối chiều điều kiện ban đầu ta được \(x=\dfrac{k\pi}{2}\)