a, ta có

(d1)=(d2)

2x-7=-x+5

\(\Leftrightarrow\)3x=12

\(\Leftrightarrow\)x=4

ta có

(d1)=(d3)

2x-7=kx+5

\(\Leftrightarrow\)2.4-7=k4+5

\(\Leftrightarrow\)k=-1

b, ta có

(d3)=(d2)

x-1=3x-5

\(\Leftrightarrow\)x=2

ta có

(d1)=(d3)

kx-7=x-1

\(\Leftrightarrow\)k2-7=2-1

\(\Leftrightarrow\)k=4

c, ta có

(d1)=(d3)

x-7=3x-1

\(\Leftrightarrow\)x=-3

ta có

(d1)=(d2)

x-7= kx-3

\(\Leftrightarrow\)-3-7=-3k-3

\(\Leftrightarrow\)k=\(\frac{7}{3}\)

Gọi pt d2 có dạng \(y=ax+b\)

Do d2 qua A và B nên ta có:

\(\left\{{}\begin{matrix}a+b=2\\-3a+b=-2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=1\end{matrix}\right.\) \(\Rightarrow d_2:y=x+1\)

Do \(d_1\) song song \(d_2\) nên chúng có cùng hệ số góc

\(\Rightarrow k=1\)

a) \(\left(d_1\right):y=mx+2m\)

 \((d_1)\parallel (d_2)\) \(\Rightarrow\left\{{}\begin{matrix}m=2m-3\\2m\ne2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m=3\\m\ne1\end{matrix}\right.\Rightarrow m=3\)

b) \(\left(d_1\right)\equiv\left(d_2\right)\Rightarrow\left\{{}\begin{matrix}m=2m-3\\2m=2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m=3\\m=1\end{matrix}\right.\Rightarrow\) không có m thỏa

c) \(\left(d_1\right)\bot\left(d_2\right)\Rightarrow m.\left(2m-3\right)=-1\Rightarrow2m^2-3m+1=0\)

\(\Rightarrow\left(m-1\right)\left(2m-1\right)=0\Rightarrow\left[{}\begin{matrix}m=1\\m=\dfrac{1}{2}\end{matrix}\right.\)

Ta có: (d1): y=m(x+2)

nên y=mx+2m

a) Để (d1)//(d2) thì \(\left\{{}\begin{matrix}m=2m-3\\2m\ne2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m-2m=-3\\m\ne1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=3\\m\ne1\end{matrix}\right.\Leftrightarrow m=3\)

b) Để (d1) trùng với (d2) thì \(\left\{{}\begin{matrix}m=2m-3\\2m=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=3\\m=1\end{matrix}\right.\Leftrightarrow m\in\varnothing\)

\(a,\Leftrightarrow\left\{{}\begin{matrix}2-m>0\\m-4>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< 2\\m>4\end{matrix}\right.\Leftrightarrow m\in\varnothing\\ b,\Leftrightarrow2-m=m-4\Leftrightarrow m=3\\ c,\Leftrightarrow2-m\ne m-4\Leftrightarrow m\ne3\)

a: Tọa độ A là nghiệm của hệ phương trình:

\(\left\{{}\begin{matrix}-x-1=x-5\\y=x-5\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}-2x=-4\\y=x-5\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=2\\y=2-5=-3\end{matrix}\right.\)

=>A(2;-3)

b: Vì \(a_1\cdot a_2=1\cdot\left(-1\right)=-1\)

nên (d1) vuông góc với (d2)

Gọi B,C lần lượt là giao điểm của (d1) với trục Oy, (d2) với trục Oy

Tọa độ B là:

\(\left\{{}\begin{matrix}x=0\\y=-x-1=-0-1=-1\end{matrix}\right.\)

=>B(0;-1)

Tọa độ C là:

\(\left\{{}\begin{matrix}x=0\\y=x-5=-5\end{matrix}\right.\)

=>C(0;-5)

B(0;-1); C(0;-5); A(2;-3)

\(BC=\sqrt{\left(-5+1\right)^2+\left(0-0\right)^2}=4\)

\(BA=\sqrt{\left(2-0\right)^2+\left(-3+1\right)^2}=2\sqrt{2}\)

\(AC=\sqrt{\left(2-0\right)^2+\left(-3+5\right)^2}=2\sqrt{2}\)

Chu vi tam giác ABC là:

\(4+2\sqrt{2}+2\sqrt{2}=4\sqrt{2}+4\)

a/

\(\Rightarrow3=4m.2-m-5\Leftrightarrow m=\dfrac{8}{5}\)

b/

Tọa độ A là \(A\left(x_0;y_0\right)\)

\(\Rightarrow y_0=4mx_0-m-5\forall m\)

\(\Leftrightarrow\left(4x_0-1\right)m-\left(y_0+5\right)=0\forall m\)

\(\Leftrightarrow\left\{{}\begin{matrix}4x_0-1=0\\y_0+5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=\dfrac{1}{4}\\y_0=-5\end{matrix}\right.\)

=> d1 luân đi qua điểm A cố định \(A\left(\dfrac{1}{4};-5\right)\forall m\)

Tọa độ B là \(B\left(x_1;y_1\right)\)

\(\Rightarrow y_1=\left(3m^2+1\right)x_1+m^2-4\forall m\)

\(\Leftrightarrow3m^2x_1+x_1+m^2-4-y_1=0\forall m\)

\(\Leftrightarrow\left(3x_1+1\right)m^2+x_1-y_1-4=0\forall m\)

\(\Leftrightarrow\left\{{}\begin{matrix}3x_1+1=0\\x_1-y_1-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-\dfrac{1}{3}\\y_1=-\dfrac{13}{3}\end{matrix}\right.\)

=> d2 luân đi qua điểm B cố định \(B\left(-\dfrac{1}{3};-\dfrac{13}{3}\right)\)

d/ d1//d2 khi

\(\left\{{}\begin{matrix}4m=3m^2+1\\-m-5\ne m^2-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m_1=1\\m_2=\dfrac{1}{3}\end{matrix}\right.\\m^2+m+1\ne0\end{matrix}\right.\)

Ta có \(m^2+m+1>0\forall m\)

\(\Rightarrow\left[{}\begin{matrix}m_1=1\\m_2=\dfrac{1}{3}\end{matrix}\right.\)

e/

\(\Rightarrow4mx-\left(m+5\right)=\left(3m^2+1\right)x+m^2-4\) tìm m để phương trình có nghiệm

Tìm giao

\(\Rightarrow4mx-\left(m+5\right)=\left(3m^2+1\right)x+m^2-4\) khi m=2

Thay m=2 tìm x rồi thay vào d1 hoặc d2 để tìm y

a: Khi m=1 thì y=(1-2)x+2*1-3

\(\Leftrightarrow y=-x-1\)

(d1): y=-x-1

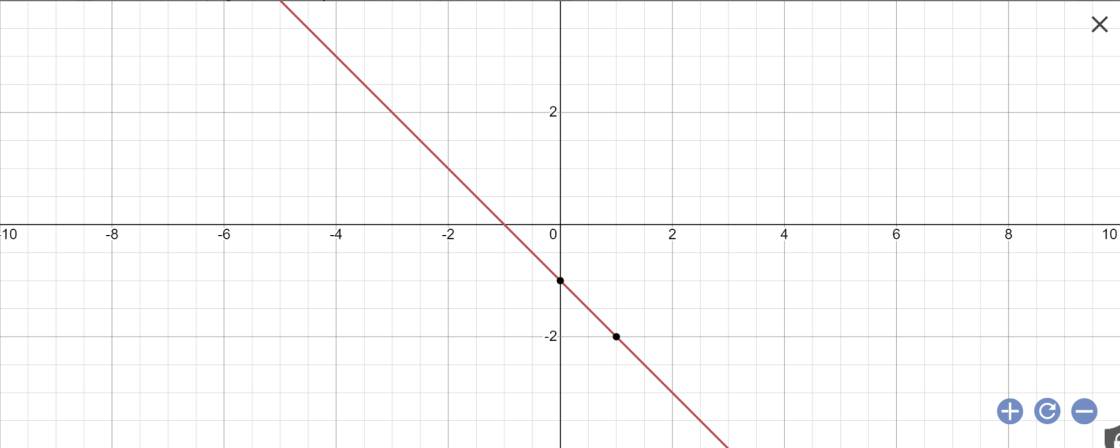
b: Tọa độ A là nghiệm của hệ phương trình sau:

\(\left\{{}\begin{matrix}-x-1=x-5\\y=x-5\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}-2x=-4\\y=x-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=2-5=-3\end{matrix}\right.\)

c: \(a_1\cdot a_2=1\cdot\left(-1\right)=-1\)

=>\(\left(d1\right)\perp\left(d2\right)\)