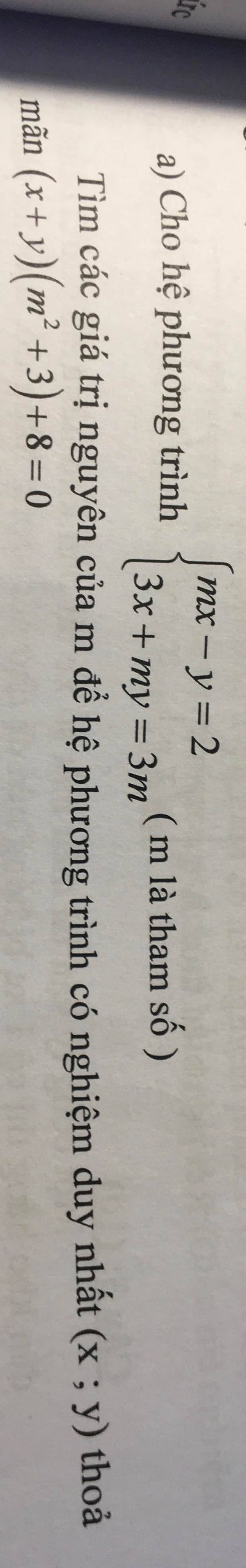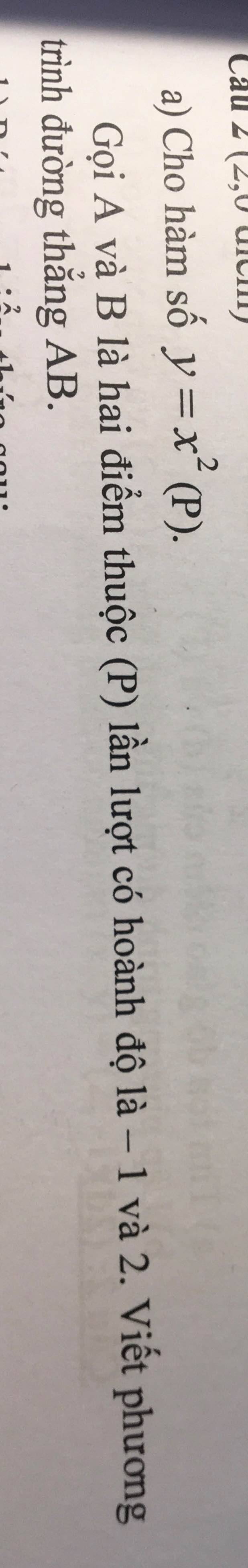Nãy gõ nhầm nên xóa rồi nhé, đáp án đây:

36, C -> most

37, A -> students

38, D -> is living

39, D -> does she

40, B -> have

36, C -> most

37, A -> students

38, D -> is living in

39, D -> does she

40, B -> have

Tham khảo:

       Ve kêu đã tự khi nào
Mà ta cứ nghĩ mới vào đầu thu
 Trường mới giờ đã thành xưa 
Ngày nào mới đến giờ xa mất rồi
     Bốn năm cứ nghĩ là dài
Cứ nghĩ học mãi học hoài chả xong
     Bây giờ lại nhớ lại mong
Mái trường xưa cũ phượng hồng mùa thi.

Bài 1:

$M, N$ lần lượt là trung điểm của $AB,AC$ nên $MN$ là đường trung bình của tam giác $ABC$ ứng với cạnh $BC$

\(\Rightarrow \left\{\begin{matrix} MN=\frac{BC}{2}\\ MN\parallel BC\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} MN=BP\\ MN\parallel BP\end{matrix}\right.\)

Tứ giác $BMNP$ có cặp cạnh đối $MN, BP$ vừa song song vừa bằng nhau nên là hình bình hành (đpcm)

Bài 2:

a) Xét tam giác $ABF$ và $CDE$ có:

$AB=CD$ (do $ABCD$ là hbh)

$BF=DE$ (gt)
$\widehat{ABF}=\widehat{CDE}$ (hai góc so le trong với $AB\parallel CD$)

$\Rightarrow \triangle ABF=\triangle CDE$ (c.g.c)

$\Rightarrow AF=CE(1)$

Mặt khác, từ tam giác bằng nhau trên cũng có $\widehat{AFB}=\widehat{CED}$

$\Rightarrow 180^0-\widehat{AFB}=180^0-\widehat{CED}$

$\Rightarrow \widehat{AFE}=\widehat{FEC}$

Hai góc này ở vị trí so le trong nên $AF\parallel CE(2)$

Từ $(1);(2)\Rightarrow AECF$ là hbh.

b) $AECF$ là hbh nên 2 đường chéo $AC, EF$ cắt nhau tại trung điểm mỗi đường.

Mà $O$ là trung điểm $AC$ nên $O$ cũng là trung điểm $EF$.

Hay $O,E,F$ thẳng hàng.

Câu 1:

b) Ta có: \(2n-3⋮n+1\)

\(\Leftrightarrow2n+2-5⋮n+1\)

Vì \(2n+2=2\left(n+1\right)⋮n+1\)

nên \(-5⋮n+1\)

\(\Leftrightarrow n+1\inƯ\left(-5\right)\)

\(\Leftrightarrow n+1\in\left\{1;-1;5;-5\right\}\)

\(\Leftrightarrow n\in\left\{0;-2;4;-6\right\}\)(tm)

Vậy: \(n\in\left\{0;-2;4;-6\right\}\)

Câu 5:

\(2x+\frac{1}{7}=\frac{1}{y}\)

\(\Rightarrow\frac{2x}{1}+\frac{1}{7}=\frac{1}{y}\)

\(\Rightarrow\frac{2x.7}{1.7}+\frac{1}{7}=\frac{1}{y}\)

\(\Rightarrow\frac{14x}{7}+\frac{1}{7}=\frac{1}{y}\)

\(\Rightarrow\frac{14x+1}{7}=\frac{1}{y}.\)

\(\Rightarrow\left(14x+1\right).y=1.7\)

\(\Rightarrow\left(14x+1\right).y=7\)

Vì \(x,y\in Z\Rightarrow\left\{{}\begin{matrix}14x+1\in Z\\y\in Z\end{matrix}\right.\)

\(\Rightarrow14x+1\inƯC\left(7\right);y\inƯC\left(7\right)\)

\(\Rightarrow14x+1\in\left\{1;-1;7;-7\right\};y\in\left\{1;-1;7;-7\right\}.\)

Đến đoạn này thì bạn tự lập bảng ra nhé, cái nào là số nguyên thì lấy.

Chúc bạn học tốt!

1 were you doing

2 were having - rang

3 takes - is celebrated 

4 was formed

5 have lost - haven't found

6 is held to worship

7 skating

8 getting up

9 reading - doing

10 has been built

11 swimming - feel

12 were watching - failed

13 has worked - graduated

14 have been invited

15 will be discussing

16 decided not to stay

17 to pass - testing

18 not to phone

19 doing

20 to stay - do

Để hệ phương trình có nghiệm duy nhất thì \(\dfrac{m}{3}< >-\dfrac{1}{m}\)

=>\(m^2\ne-3\)(luôn đúng)

Ta có: \(\left\{{}\begin{matrix}mx-y=2\\3x+my=3m\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=mx-2\\3x+m\left(mx-2\right)=3m\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=mx-2\\3x+m^2x-2m=3m\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=mx-2\\x\left(m^2+3\right)=5m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5m}{m^2+3}\\y=m\cdot\dfrac{5m}{m^2+3}-2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=\dfrac{5m}{m^2+3}\\y=\dfrac{5m^2-2m^2-6}{m^2+3}=\dfrac{3m^2-6}{m^2+3}\end{matrix}\right.\)

\(\left(x+y\right)\cdot\left(m^2+3\right)+8=0\)

=>\(\dfrac{5m+3m^2-6}{m^2+3}\cdot\left(m^2+3\right)+8=0\)

=>\(3m^2+5m-6+8=0\)

=>\(3m^2+5m+2=0\)

=>(m+1)(3m+2)=0

=>\(\left[{}\begin{matrix}m=-1\\m=-\dfrac{2}{3}\end{matrix}\right.\)

Bài 2:

Thay x=-1 vào (P), ta được:

\(y=\left(-1\right)^2=1\)

Thay x=2 vào (P), ta được:

\(y=2^2=4\)

vậy: A(-1;1); B(2;4)

Gọi (d): y=ax+b(a\(\ne\)0) là phương trình đường thẳng AB

Thay x=-1 và y=1 vào (d), ta được:

\(a\cdot\left(-1\right)+b=1\)

=>-a+b=1(1)

Thay x=2 và y=4 vào (d), ta được:

\(2\cdot a+b=4\)

=>2a+b=4(2)

Từ (1) và (2) ta có hệ phương trình: \(\left\{{}\begin{matrix}-a+b=1\\2a+b=4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}-3a=-3\\-a+b=1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}a=1\\b=a+1=1+1=2\end{matrix}\right.\)

Vậy: phương trình AB là y=x+2

7. A = (x + y)^2 - 4y^2

= (x + y - 2y)(x + y + 2y)

= (x - y)(x + 3y)

2. x^4 + 4

= x^4 + 4x^2 + 4 - 4x^2

= (x^2 + 2)^2 - (2x)^2

= (x^2 + 2x + 2)(x^2 - 2x + 2)

3. 4x^4 + 16

= 4(x^4 + 4)

= 4(x^2 + 2x + 2)(x^2 - 2x + 2)

????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????

?