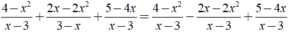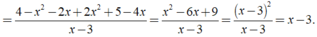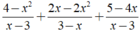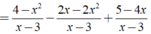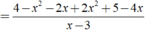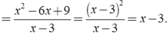2x23+√(4x29x+2)=2√(x+2)+√(4x+1)

Những câu hỏi liên quan
2(x-51)=2x23+20
giúp mk nha các bn
`2(x-51) = 2*2^3+20`
`=>2(x-51) = 2*8+20`
`=>2(x-51) =16+20`
`=>2(x-51) =36`
`=> x-51=36:2`
`=>x-51= 18`
`=>x=18+51`
`=> x= 69`
Đúng 2
Bình luận (0)
\(2\left(x-51\right)=2\cdot2^3+20\)
\(x-51=2^3+10\)
\(x-51=18\)
\(x=18+51\)
\(x=69\)
Đúng 1
Bình luận (0)
\(2(x-51)=2\cdot2^3+20\\2(x-51)=2\cdot8+20\\2(x-51)=16+20\\2(x-51)=36\\x-51=36:2\\x-51=18\\x=18+51\\x=69\)
Đúng 0
Bình luận (0)
Rút gọn biểu thức
4
-
x
2
x
-
3
+
2
x
-
2
x
2
3
-
x
+
5
-
4
x
x
-...
Đọc tiếp
Rút gọn biểu thức 4 - x 2 x - 3 + 2 x - 2 x 2 3 - x + 5 - 4 x x - 3 được kết quả là
A. 3 - x.
B. x - 3
C. x + 3.
D. - x - 3.
Rút gọn biểu thức
4
-
x
2
x
-
3
+
2
x
-
2
x
2
3
-
x
+
5
-
4
x
x
-...
Đọc tiếp
Rút gọn biểu thức 4 - x 2 x - 3 + 2 x - 2 x 2 3 - x + 5 - 4 x x - 3 được kết quả là
A. 3 - x.
B. x - 3
C. x + 3.
D. - x - 3.
Câu 1
a) 6/7+3/14=?
b) 2/5+5=?
Câu 2
a) y x 2/3=6/5
y = ?
b) y+2/7 =5/6
y =
Câu 3
Một mảnh đất hình chữ nhật có chu vi là 96m ,chiều dài bằng 7/5 chiều rộng . Tính diện tich hình chữ nhật.
Câu 4 Tính nhanh
1/2x23=1/9x1/2
Câu 5
3/5 tấn = ?kg
hepe me !!!!!!!!!!!!!!!!
a) đáp án là 15/14 hoặc 1 1/4
b) đáp án là 27/5 hoặc 5 2/5. Hok tốt!!:)
55+308496843-984730264784087394758674+2x23=????
Xem thêm câu trả lời
`c)(2x-1)^{2}+(1-x).3x<=(x+2)^{2}`
`<=>>4x^{2}-4x+1+3x-3x^{2}<=x^{2}+4x+4`
`<=>x^{2}-x+1<=x^{2}+4x+4`
`<=>4x+x>=1-4`
`<=>5x>=-3`
`<=>x>=-3/5`
thứ nhất bn đăng sai môn
thứ hai bn giải r đăng lmj :???
Đúng 1
Bình luận (0)
Thứ nhất đang sai môn
Thứ hai không biết giải fndf]-0jhdfuhiofghjfgoihjfgopihjfgihjohjgo;hjghghgdjhldhjdfighjs;dligjlkdfgjdhfghfgh41fg6j541fg3j5h4gf6j54dgh65gf4654j
5gj5fg
35j4gh
6jfd4
5j4fj
1.\(\sqrt{x^2-4x+3}=x-2\)
2.\(\sqrt{4x^2-4x+1}=x-1\)
3. \(2x-\sqrt{4x-1}=0\)
4. \(x-2\sqrt{x-1}=16\)
1. \(\sqrt{x^2-4x+3}=x-2\)
<=> x2 - 4x + 3 = (x - 2)2
<=> x2 - 4x + 3 = x2 - 4x + 4
<=> x2 - x2 - 4x + 4x = 1
<=> 0 = 1 (Vô lí)
vậy PT có nghiệm là S = \(\varnothing\)
Đúng 2
Bình luận (0)
2. \(\sqrt{4x^2-4x+1}=x-1\)
<=> \(\sqrt{\left(2x-1\right)^2}=x-1\)
<=> 2x - 1 = x - 1
<=> 2x - x = -1 + 1
<=> x = 0
Đúng 2
Bình luận (0)
1: ta có: \(\sqrt{x^2-4x+3}=x-2\)
\(\Leftrightarrow x^2-4x+3=x^2-4x+4\)(vô lý)
2: Ta có: \(\sqrt{4x^2-4x+1}=x-1\)
\(\Leftrightarrow\left(2x-1-x+1\right)\left(2x-1+x-1\right)=0\)
\(\Leftrightarrow x\left(3x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=\dfrac{2}{3}\left(loại\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Giải phương trình:1. x^4-6x^2-12x-802. dfrac{x}{2x^2+4x+1}+dfrac{x}{2x^2-4x+1}dfrac{3}{5}3. x^4-x^3-8x^2+9x-9+left(x^2-x+1right)sqrt{x+9}04. 2x^2.sqrt{-4x^4+4x^2+3}4x^4+15. x^2+4x+3sqrt{dfrac{x}{8}+dfrac{1}{2}}6. left{{}begin{matrix}4x^3+xy^23x-y4xy+y^22end{matrix}right.7. left{{}begin{matrix}sqrt{x^2-3y}left(2x+y+1right)+2x+y-505x^2+y^2+4xy-3y-50end{matrix}right.8. left{{}begin{matrix}sqrt{2x^2+2}+left(x^2+1right)^2+2y-100left(x^2+1right)^2+x^2yleft(y-4right)0end{matrix}right.
Đọc tiếp
Giải phương trình:
1. \(x^4-6x^2-12x-8=0\)
2. \(\dfrac{x}{2x^2+4x+1}+\dfrac{x}{2x^2-4x+1}=\dfrac{3}{5}\)
3. \(x^4-x^3-8x^2+9x-9+\left(x^2-x+1\right)\sqrt{x+9}=0\)
4. \(2x^2.\sqrt{-4x^4+4x^2+3}=4x^4+1\)
5. \(x^2+4x+3=\sqrt{\dfrac{x}{8}+\dfrac{1}{2}}\)
6. \(\left\{{}\begin{matrix}4x^3+xy^2=3x-y\\4xy+y^2=2\end{matrix}\right.\)
7. \(\left\{{}\begin{matrix}\sqrt{x^2-3y}\left(2x+y+1\right)+2x+y-5=0\\5x^2+y^2+4xy-3y-5=0\end{matrix}\right.\)
8. \(\left\{{}\begin{matrix}\sqrt{2x^2+2}+\left(x^2+1\right)^2+2y-10=0\\\left(x^2+1\right)^2+x^2y\left(y-4\right)=0\end{matrix}\right.\)
1.
\(x^4-6x^2-12x-8=0\)
\(\Leftrightarrow x^4-2x^2+1-4x^2-12x-9=0\)
\(\Leftrightarrow\left(x^2-1\right)^2=\left(2x+3\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-1=2x+3\\x^2-1=-2x-3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-2x-4=0\\x^2+2x+2=0\end{matrix}\right.\)
\(\Leftrightarrow x=1\pm\sqrt{5}\)
Đúng 5
Bình luận (0)
3.
ĐK: \(x\ge-9\)
\(x^4-x^3-8x^2+9x-9+\left(x^2-x+1\right)\sqrt{x+9}=0\)
\(\Leftrightarrow\left(x^2-x+1\right)\left(\sqrt{x+9}+x^2-9\right)=0\)
\(\Leftrightarrow\sqrt{x+9}+x^2-9=0\left(1\right)\)
Đặt \(\sqrt{x+9}=t\left(t\ge0\right)\Rightarrow9=t^2-x\)
\(\left(1\right)\Leftrightarrow t+x^2+x-t^2=0\)
\(\Leftrightarrow\left(x+t\right)\left(x-t+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-t\\x=t-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\sqrt{x+9}\\x=\sqrt{x+9}-1\end{matrix}\right.\)
\(\Leftrightarrow...\)
Đúng 5
Bình luận (2)
2.
ĐK: \(x\ne\dfrac{2\pm\sqrt{2}}{2};x\ne\dfrac{-2\pm\sqrt{2}}{2}\)
\(\dfrac{x}{2x^2+4x+1}+\dfrac{x}{2x^2-4x+1}=\dfrac{3}{5}\)
\(\Leftrightarrow\dfrac{1}{2x+\dfrac{1}{x}+4}+\dfrac{1}{2x+\dfrac{1}{x}-4}=\dfrac{3}{5}\)
Đặt \(2x+\dfrac{1}{x}+4=a;2x+\dfrac{1}{x}-4=b\left(a,b\ne0\right)\)
\(pt\Leftrightarrow\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{3}{5}\left(1\right)\)
Lại có \(a-b=8\Rightarrow a=b+8\), khi đó:
\(\left(1\right)\Leftrightarrow\dfrac{1}{b+8}+\dfrac{1}{b}=\dfrac{3}{5}\)
\(\Leftrightarrow\dfrac{2b+8}{\left(b+8\right)b}=\dfrac{3}{5}\)
\(\Leftrightarrow10b+40=3\left(b+8\right)b\)
\(\Leftrightarrow\left[{}\begin{matrix}b=2\\b=-\dfrac{20}{3}\end{matrix}\right.\)
TH1: \(b=2\Leftrightarrow...\)
TH2: \(b=-\dfrac{20}{3}\Leftrightarrow...\)
Đúng 3
Bình luận (0)
Xem thêm câu trả lời
Rút gọn các biểu thức sau:
a) ((1/x^2+4x+4)-(1/x^2-4x+4)):((1/x+2)+(1/x^2-2))
b)((2x/2x-y)-(4x^2/4x^2+4xy+y^2)):((2x/4x^2-y^2)+(1/y-2x))
a,sửa đề : \(\left(\frac{1}{x^2+4x+4}-\frac{1}{x^2-4x+4}\right):\left(\frac{1}{x+2}+\frac{1}{x^2-4}\right)\)
\(=\left(\frac{1}{\left(x+2\right)^2}-\frac{1}{\left(x-2\right)^2}\right):\left(\frac{x-2+1}{\left(x+2\right)\left(x-2\right)}\right)\)
\(=\left(\frac{x^2-4x+4-x^2-4x-4}{\left(x+2\right)^2\left(x-2\right)^2}\right):\left(\frac{x-1}{\left(x+2\right)\left(x-2\right)}\right)\)
\(=\frac{-8x\left(x+2\right)\left(x-2\right)}{\left(x+2\right)^2\left(x-2\right)^2\left(x-1\right)}=\frac{-8x}{\left(x-1\right)\left(x^2-4\right)}\)
b, \(\left(\frac{2x}{2x-y}-\frac{4x^2}{4x^2+4xy+y^2}\right):\left(\frac{2x}{4x^2-y^2}+\frac{1}{y-2x}\right)\)
\(=\left(\frac{2x}{2x-y}-\frac{4x^2}{\left(2x+y\right)^2}\right):\left(\frac{2x}{\left(2x-y\right)\left(2x+y\right)}-\frac{1}{2x-y}\right)\)
\(=\left(\frac{2x\left(2x+y\right)^2-4x^2\left(2x-y\right)}{\left(2x-y\right)\left(2x+y\right)^2}\right):\left(\frac{2x-\left(2x+y\right)}{\left(2x-y\right)\left(2x+y\right)}\right)\)
\(=\left(\frac{8x^3+8x^2y+2xy^2-8x^3+4x^2y}{\left(2x-y\right)\left(2x+y\right)^2}\right):\left(\frac{-y}{\left(2x-y\right)\left(2x+y\right)}\right)\)
\(=-\left(\frac{12x^2y+xy^2}{2x+y}\right)=\frac{-12x^2y-xy^2}{2x+y}\)
a) 1-4x^2/x^2+4x : 2-4x/3x
b) x+1/x+2 : x+2/x+3 : x+3/x+1
c)x+1/x+2 : (x+2/x+3 : x+3/x+1)
d) (1/x^2+x - 2-2x/x+1):(1/x+x-2)
e) 5x-15/4x+4 : x^2-9/x^2+2x+1