a, \(sin4x.cosx-sin3x=0\)

\(\Leftrightarrow\dfrac{1}{2}sin5x+\dfrac{1}{2}sin3x-sin3x=0\)

\(\Leftrightarrow sin5x=sin3x\)

\(\Leftrightarrow\left[{}\begin{matrix}5x=3x+k2\pi\\5x=\pi-3x+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\dfrac{\pi}{8}+\dfrac{k\pi}{4}\end{matrix}\right.\)

b, \(sin2x+\sqrt{3}cos2x=\sqrt{2}\)

\(\Leftrightarrow\dfrac{1}{2}sin2x+\dfrac{\sqrt{3}}{2}cos2x=\dfrac{\sqrt{2}}{2}\)

\(\Leftrightarrow sin\left(2x+\dfrac{\pi}{3}\right)=\dfrac{\sqrt{2}}{2}\)

\(\Leftrightarrow\left[{}\begin{matrix}2x+\dfrac{\pi}{3}=\dfrac{\pi}{4}+k2\pi\\2x+\dfrac{\pi}{3}=\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{24}+k\pi\\x=\dfrac{5\pi}{24}+k\pi\end{matrix}\right.\)

(sin²x - 4cos²x)(sin²x - 2sinx.cosx) = 2cos⁴x

⇔ (5sin²x - 4)(sin²x - sin2x) = 2cos⁴x
⇔ \(\left(\dfrac{5-5cos2x}{2}-4\right)\left(\dfrac{1-cos2x}{2}-sin2x\right)\)= 2cos⁴x

⇔ \(\dfrac{5-5cos2x-8}{2}.\dfrac{1-cos2x-2sin2x}{2}\) = 2cos⁴x

⇔ (5cos2x + 3)(cos2x + 2sin2x - 1) = 8cos⁴x

⇔ 5cos²2x + 5cos2x.sin2x + 3cos2x + 6sin2x - 3 = 8cos⁴x

⇔ 5.\(\dfrac{1+cos4x}{2}\) + \(\dfrac{5}{2}sin4x\) + 3cos2x + 6sin2x - 3 = 8cos⁴x

⇔ \(\dfrac{5}{2}cos4x+\dfrac{5}{2}sin4x+3cos2x+6sin2x-\dfrac{1}{2}\) = 8cos⁴x

⇔ 5cos4x + 5sin4x + 6cos2x + 12sin2x - 1 = 16cos⁴x

VP = 16cos⁴x = 16 . \(\dfrac{\left(1+cos2x\right)^2}{4}\) = 4. (1 + cos2x)²

VP = 4 . (1 + 2cos2x + cos²2x)

VP = 4 + 8cos2x + 4 . \(\dfrac{1+cos4x}{2}\)

VP = 6 + 8cos2x+ 2cos4x

Vậy 3cos4x + 5sin4x - 2cos2x + 12sin2x - 7 = 0

@Nguyễn Việt Lâm giúp em với

\( 2)\sin x + \sin 2x + \sin 3x = 0\\ \Leftrightarrow 2\sin 2x.\cos x + \sin 2x = 0\\ \Leftrightarrow \sin 2x\left( {2\cos x + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l} \sin 2x = 0\\ 2\cos x + 1 = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} 2x = k\pi \\ \cos x = \dfrac{{ - 1}}{2} \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = \dfrac{{k\pi }}{2}\\ x = \pm \dfrac{{2\pi }}{3} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z} } \right) \)

\( 3)\sin x + \sin 2x + \sin 3x + \sin 4x = 0\\ \Leftrightarrow \left( {\sin x + \sin 4x} \right) + \left( {\sin 2x + \sin 3x} \right) = 0\\ \Leftrightarrow 2\sin \dfrac{{5x}}{2}.\cos \dfrac{{3x}}{2} + 2\sin \dfrac{{5x}}{2}.\cos \dfrac{x}{2} = 0\\ \Leftrightarrow \sin \dfrac{{5x}}{2}.\left( {\cos \dfrac{{3x}}{2} + \cos \dfrac{x}{2}} \right) = 0\\ \Leftrightarrow \sin \dfrac{{5x}}{2}.2\cos x.\cos \dfrac{x}{2} = 0\\ \Leftrightarrow \left[ \begin{array}{l} \sin \dfrac{{5x}}{2} = 0\\ 2\cos x = 0\\ \cos \dfrac{x}{2} = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = \dfrac{{2k\pi }}{5}\\ x = \dfrac{\pi }{2} + k\pi \\ x = \pi + 2k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right) \)

a) Vì \(\sin \frac{\pi }{6} = \frac{1}{2}\) nên ta có phương trình \(sin2x = \sin \frac{\pi }{6}\)

\( \Leftrightarrow \left[ \begin{array}{l}2x = \frac{\pi }{6} + k2\pi \\2x = \pi  - \frac{\pi }{6} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{{12}} + k\pi \\x = \frac{{5\pi }}{{12}} + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)

\(\begin{array}{l}b,\,\,sin(x - \frac{\pi }{7}) = sin\frac{{2\pi }}{7}\\ \Leftrightarrow \left[ \begin{array}{l}x - \frac{\pi }{7} = \frac{{2\pi }}{7} + k2\pi \\x - \frac{\pi }{7} = \pi  - \frac{{2\pi }}{7} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{{3\pi }}{7} + k2\pi \\x = \frac{{6\pi }}{7} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)

\(\begin{array}{l}\;c)\;sin4x - cos\left( {x + \frac{\pi }{6}} \right) = 0\\ \Leftrightarrow sin4x = cos\left( {x + \frac{\pi }{6}} \right)\\ \Leftrightarrow sin4x = \sin \left( {\frac{\pi }{2} - x - \frac{\pi }{6}} \right)\\ \Leftrightarrow sin4x = \sin \left( {\frac{\pi }{3} - x} \right)\\ \Leftrightarrow \left[ \begin{array}{l}4x = \frac{\pi }{3} - x + k2\pi \\4x = \pi  - \frac{\pi }{3} + x + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{{15}} + k\frac{{2\pi }}{5}\\x = \frac{{2\pi }}{9} + k\frac{{2\pi }}{3}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)

Chọn C

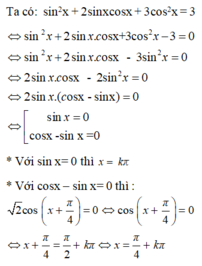
Vậy các nghiệm thuộc khoảng (0, 2π) là  π 4 , π , 5 π 4

\(\text{c) }sin3x-\sqrt{3}cos3x=2cos5x\\ \Leftrightarrow\frac{1}{2}sin3x-\frac{\sqrt{3}}{2}cos3x=cos5x\\ \Leftrightarrow sin\frac{\pi}{6}\cdot sin3x-cos\frac{\pi}{6}\cdot cos3x=cos5x\\ \Leftrightarrow cos\left(3x+\frac{\pi}{6}\right)=-cos5x\\ \Leftrightarrow cos\left(3x+\frac{\pi}{6}\right)=cos\left(\pi-5x\right)\\ \Leftrightarrow\left[{}\begin{matrix}3x+\frac{\pi}{6}=\pi-5x+m2\pi\\3x+\frac{\pi}{6}=5x-\pi+n2\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\frac{5\pi}{48}+\frac{m\pi}{4}\\x=\frac{7\pi}{12}-n\pi\end{matrix}\right.\)

\(d\text{) }sinx\left(sinx+2cosx\right)=2\\ \Leftrightarrow cos^2x+\left(sinx-cosx\right)^2=0\\ \Leftrightarrow cosx=sinx=0\left(VN\right)\)

\(e\text{) }\sqrt{3}\left(sin2x+cos7x\right)=sin7x-cos2x\\ \Leftrightarrow\sqrt{3}sin2x+cos2x=sin7x-\sqrt{3}cos7x\\ \Leftrightarrow sin2x\cdot\frac{\sqrt{3}}{2}+cos2x\cdot\frac{1}{2}=sin7x\cdot\frac{1}{2}-cos7x\cdot\frac{\sqrt{3}}{2}\\ \Leftrightarrow sin2x\cdot cos\frac{\pi}{3}+cos2x\cdot sin\frac{\pi}{3}=sin7x\cdot cos\frac{\pi}{3}-cos7x\cdot sin\frac{\pi}{3}\\ \Leftrightarrow sin\left(2x-\frac{\pi}{3}\right)=sin\left(7x-\frac{\pi}{3}\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-\frac{\pi}{3}=7x-\frac{\pi}{3}+m2\pi\\2x-\frac{\pi}{3}=\frac{4\pi}{3}-7x+n2\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\frac{-m2\pi}{5}\\x=\frac{5\pi}{27}+\frac{n2\pi}{9}\end{matrix}\right.\)

\(\text{a) }\sqrt{3}sin2x-cos2x+1=0\\ \Leftrightarrow\frac{\sqrt{3}}{2}sin2x-\frac{1}{2}cos2x=-\frac{1}{2}\\ \Leftrightarrow cos\frac{\pi}{3}\cdot cos2x-sin\frac{\pi}{3}\cdot sin2x=\frac{1}{2}\\ \Leftrightarrow cos\left(2x-\frac{\pi}{3}\right)=cos\frac{\pi}{3}\\ \Leftrightarrow\left[{}\begin{matrix}2x-\frac{\pi}{3}=\frac{\pi}{3}+m2\pi\\2x-\frac{\pi}{3}=-\frac{\pi}{3}+n2\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{3}+m\pi\\x=n\pi\end{matrix}\right.\)

\(\text{b) }pt\Leftrightarrow sin4x=\frac{1-4cosx}{3}\\ \Leftrightarrow sin^24x+cos^24x=\left(\frac{1-cos4x}{3}\right)^2+cos^24x=1\\ \Leftrightarrow\left[{}\begin{matrix}cos4x=1\\cos4x=-\frac{4}{5}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}cos4x=1\\cos4x=-\frac{4}{5}\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\frac{k\pi}{2}\\x=\frac{arccos\left(-\frac{4}{5}\right)}{4}+\frac{k\pi}{2}\end{matrix}\right.\)

Phương trình:

3   sin 2 x + 2 sin x cos x - cos 2 x = 0 (*).

cos x = 0 ⇒   sin 2 x = 1  không phải là nghiệm của phương trình (*).

cos x ≠ 0 . Ta có: 

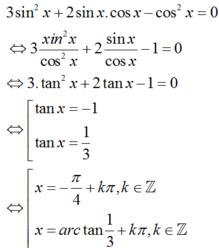
Nghiệm nguyên dương nhỏ nhất của phương trình là   x 0 ∈ 0 ; π 2

Chọn C.

a) cosx - √3sinx = √2 ⇔ cosx - tansinx = √2

⇔ coscosx - sinsinx = √2cos ⇔ cos(x + ) =

⇔

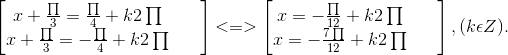
b) 3sin3x - 4cos3x = 5 ⇔ sin3x - cos3x = 1.

Đặt α = arccos thì phương trình trở thành

cosαsin3x - sinαcos3x = 1 ⇔ sin(3x - α) = 1 ⇔ 3x - α = + k2π

⇔ x = , k ∈ Z (trong đó α = arccos).

c) Ta có sinx + cosx = √2cos(x - ) nên phương trình tương đương với

2√2cos(x - ) - √2 = 0 ⇔ cos(x - ) =

⇔

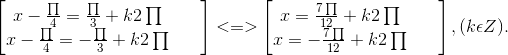
d) 5cos2x + 12sin2x -13 = 0 ⇔

Đặt α = arccos thì phương trình trở thành

cosαcos2x + sinαsin2x = 1 ⇔ cos(2x - α) = 1

⇔ x = + kπ, k ∈ Z (trong đó α = arccos).