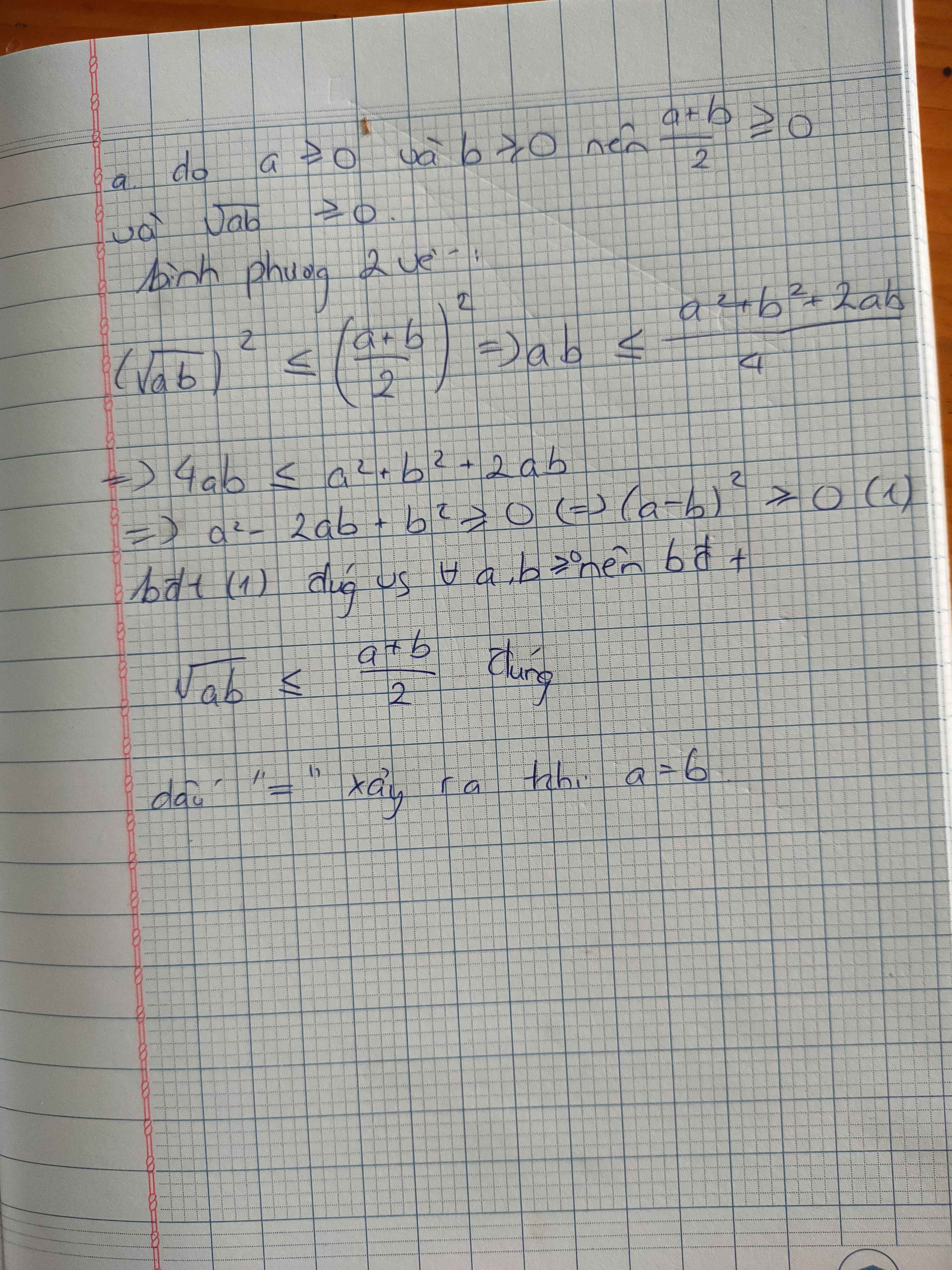Cho 3a+5b=12 . Tìm giá trị lớn nhất của \(B=ab\)

Những câu hỏi liên quan
Cho a, b > 0 và 3a + 5b = 12. Tìm giá trị lớn nhất của tích P = ab.
Áp dụng BĐT Côsi cho 2 số dương, ta có:
\(3a+5b=12\ge2\sqrt{3a.5b}=2\sqrt{15ab}\)
\(\Leftrightarrow\sqrt{15ab}\le6\)
\(\Leftrightarrow ab\le\dfrac{36}{15}\)
Dấu "=" \(\Leftrightarrow\left\{{}\begin{matrix}3a=5b\\3a+5b=12\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=2\\b=\dfrac{6}{5}\end{matrix}\right.\)
Đúng 1
Bình luận (1)
Cho a, b > 0 và 3a + 5b = 12. Tìm giá trị lớn nhất của tích P = ab.
Theo BĐT cosi ta có:
\(3a+5b\ge2\sqrt{3a\cdot5b}\)
\(\Leftrightarrow3a+5b\ge2\sqrt{15ab}\)
\(\Leftrightarrow12\ge2\sqrt{15ab}\)
\(\Leftrightarrow\sqrt{15ab}\le\dfrac{12}{2}\)
\(\Leftrightarrow\sqrt{15ab}\le6\)
\(\Leftrightarrow15ab\le36\)
\(\Leftrightarrow ab\le\dfrac{36}{15}\)
\(\Leftrightarrow ab\le\dfrac{12}{5}\)
\(\Rightarrow P\le\dfrac{12}{5}\)
Vậy: \(P_{max}=\dfrac{12}{5}\)
Đúng 2
Bình luận (0)
Để tìm giá trị lớn nhất của tích P = ab, ta có thể sử dụng phương pháp đạo hàm. Đầu tiên, ta sẽ giải hệ phương trình 3a + 5b = 12 để tìm giá trị của a và b. 3a + 5b = 12 Tiếp theo, ta sẽ giải phương trình trên theo a: 3a = 12 - 5b a = (12 - 5b)/3 Sau đó, ta sẽ thay giá trị của a vào biểu thức tích P = ab: P = ((12 - 5b)/3) * b Tiếp theo, ta sẽ đạo hàm của P theo b: dP/db = (12 - 5b)/3 - (5b)/3 Để tìm giá trị lớn nhất của P, ta sẽ giải phương trình dP/db = 0: (12 - 5b)/3 - (5b)/3 = 0 12 - 5b - 5b = 0 12 - 10b = 0 10b = 12 b = 12/10 b = 6/5 Sau đó, ta sẽ thay giá trị của b vào biểu thức tích P = ab: P = ((12 - 5(6/5))/3) * (6/5) P = (12 - 6)/3 * 6/5 P = 6/3 * 6/5 P = 12/5 Vậy, giá trị lớn nhất của tích P = ab là 12/5....
Đúng 0
Bình luận (1)
Cho a, b > 0 và 3a + 5b = 12. Tìm giá trị lớn nhất của tích P = ab.
\(12=3a+5b\ge2\sqrt{3a.5b}=2\sqrt{15ab}\Rightarrow ab\le\frac{36}{15}=\frac{12}{5}\)
Dấu " = " xảy ra khi \(3a=5b;3a+5b=12\Leftrightarrow a=2;b=\frac{6}{5}\)
Nguồn: Mr Lazy
Cho a, b > 0 và 3a + 5b = 12. Tìm giá trị lớn nhất của tích P = ab.
c) Cho a, b > 0 và 3a + 5b = 12. Tìm giá trị lớn nhất của tích P = ab.
Cho a, b > 0 và 3a + 5b = 12. Tìm giá trị lớn nhất của tích P = ab.
\(12=3a+5b\ge2\sqrt{3a.5b}=2\sqrt{15ab}\Rightarrow ab\le\frac{36}{15}=\frac{12}{5}\)
Dấu "=" xảy ra khi \(3a=5b;\text{ }3a+5b=12\Leftrightarrow a=2;\text{ }b=\frac{6}{5}\)
Đúng 1
Bình luận (0)
Cho x + y = 2. Tìm giá trị nhỏ nhất của biểu thức: S = x2 + y2.
Cho a, b > 0 và 3a + 5b = 12. Tìm giá trị lớn nhất của tích P = ab.
BÀI 1 : cho x+y=2 ................
GIẢI :
TA CÓ :x2+y2\(\ge\)\(\frac{\left(x+2\right)^2}{2}\)=2
MIN =2 khi x=y=1
BÀI 2: cho a,b>0 và ...........
GIẢI:
12=3a+5b \(\ge\)2\(\sqrt{3a.5b}\)
\(=2\sqrt{15ab}=>ab\le\frac{36}{15}=\frac{12}{15}\)
dấu "=" xảy ra khi 3a=5b,3a+5b=12
<=>a=2,b=6/5
tk mk nha !\(\phi\Phi\alpha\omega\Phi\varepsilon\partial\beta\)
Đúng 0
Bình luận (0)
a) Cho a ≥ 0, b ≥ 0. Chứng minh bất đẳng thức Cauchy: ![]()
b) Cho a, b, c > 0. Chứng minh rằng: ![]()
c) Cho a, b > 0 và 3a + 5b = 12. Tìm giá trị lớn nhất của tích P = ab
\(\left(\sqrt{a}-\sqrt{b}\right)^2\ge0\Leftrightarrow a+b-2\sqrt{ab}\ge0\Leftrightarrow a+b\ge2\sqrt{ab}\Leftrightarrow\frac{a+b}{2}\ge\sqrt{ab}\)
Đúng 2
Bình luận (0)
Cho a, b > 0 và 3a + 5b = 12.
Giá trị lớn nhất của biểu thức P = ab là ...........
P = \(\frac{1}{15}\left(3a\right)\left(5b\right)\le\frac{1}{15}\cdot\frac{\left(3a+5b\right)^2}{4}=\frac{12}{5}\)
Đúng 0
Bình luận (0)
ta có \(12=3a+5b\ge2\sqrt{3a\cdot5b}=2\sqrt{15ab}\)
==> \(ab\le\frac{36}{15}=\frac{12}{5}\)
dấu '=' xảy ra khi a;b thỏa mãn hệ pt \(3a=5bva3a+5b=12\)
=>a=2; b=6/5
Đúng 0
Bình luận (0)
có 1 cách giải đối với các dạng toán tìm min, max vô cùng hay và dễ nhớ, ứng dụng được đối với hầu như các bài toán min,max, muốn biết không
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho a,b là 2 số duơng thoả mãn điều kiện 3a+5b bằng 12 hãy tìm giá trị lớn nhất của biểu thức D bằng a.b
kết quả của mk là a.b=0 \(\Leftrightarrow a=4;b=0\)
Đúng 0
Bình luận (0)