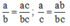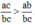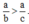cmr trong 2 số dương thì số nào lớn hơn thì có bình phương lớn hơn

Những câu hỏi liên quan
CMR: Trong 2 số dương:
a) Số nào lớn hơn thì có bình phương lớn hơn
b) Số nào có bình phương lớn hơn thì số đó lớn hơn
mình nghĩ là thế này
a)Nhân hai vế của x>y với số dương x được x^2>xy(1)
Nhân hai vế của x>y với số dương y được xy>y^2(2)
Từ (1) và (2) suy ra:
x^2>y^2
Đúng 0
Bình luận (0)
CMR: Trong 2 số dương:
a) Số nào lớn hơn thì có bình phương lớn hơn
b) Số nào có bình phương lớn hơn thì số đó lớn hơn
bạn vào olm.vn/hoi-đap/691595 , câu hỏi của 'mãi mãi là em ' nha. mik thấy có bạn trả lời rồi đó
Đúng 0
Bình luận (0)
Chứng minh rằng trong 2 số dương
a) Số nào lớn hơn thì có bình phương lớn hơn
B) Số nào có bình phương lớn hơn thì lớn hơn
Xem chi tiết
Cho x>y>0.
Nhân hai vế của x>y với số dương x ta được x2>xy (1)
Nhân 2 vế của x>y với số dương y ta được xy>y2 (2)
Từ (1) và (2) =>x2>y2
Đúng 0
Bình luận (2)
Cho x>0, y>0 và x2>y2
Giả sử x<y thì theo câu a ta có x2<y2, trái với giả thiết
Giả sử x=y thì x2=y2, trái với giả thiết
Vậy x>y
Đúng 0
Bình luận (0)
Câu 2: Muốn so sánh hai phân số không cùng mẫu, ta viết chúng dưới dạng hai phân số có cùng một mẫu dương rồi so sánh các tử với nhau:A. Phân số nào có tử lớn hơn thì phân số đó lớn hơnB. Phân số nào có mẫu lớn hơn thì phân số đó lớn hơnC. Phân số nào có tử nhỏ hơn thì phân số đó lớn hơnD. Phân số nào có mẫu nhỏ hơn thì phân số đó lớn hơn
Đọc tiếp
Câu 2: Muốn so sánh hai phân số không cùng mẫu, ta viết chúng dưới dạng hai phân số có cùng một mẫu dương rồi so sánh các tử với nhau:
A. Phân số nào có tử lớn hơn thì phân số đó lớn hơn
B. Phân số nào có mẫu lớn hơn thì phân số đó lớn hơn
C. Phân số nào có tử nhỏ hơn thì phân số đó lớn hơn
D. Phân số nào có mẫu nhỏ hơn thì phân số đó lớn hơn![]()
Trong hai mẫu số liệu, mẫu nào có phương sai lớn hơn thì có độ lệch chuẩn lớn hơn, đúng hay sai?
A. Đúng.
B. Sai.
Độ lệch chuẩn bằng căn bậc hai của phương sai.
=> Mẫu nào có phương sai lớn hơn thì có độ lệch chuẩn lớn hơn.
Chọn A.
Đúng 0
Bình luận (0)
Cho 1 dãy n số trong đó số đầu tiên và số cuối cùng bằng 0 còn các số khác thì mỗi số không lớn hơn trung bình cộng của 2 số đứng cạnh nó. Chứng minh rằng trong dãy số đó không có số nào dương.
Chứng tỏ rằng trong hai phân số cùng tử, tử và mẫu đều dương, phân số nào có mẫu nhỏ hơn thì lớn hơn.
Nếu a, b, c > 0 và b < c thì a b > a c
Chứng minh rằng trong hai phân số cùng một tử số, tử và mẫu đều dương, phân số nào có mẫu nhỏ hơn thì phân số đó lớn hơn.
Đặt lại yêu cầu đề bài :
So sánh hai phân số \(\frac{a}{b}\) và \(\frac{a}{c}\) với a, b, c \(\in\) N* và b < c.
Ta có \(\frac{a}{b}=\frac{ac}{bc}\) ; \(\frac{a}{c}=\frac{ab}{bc}\)
Do b < c và a > 0 nên ab < ac.
Vậy \(\frac{ac}{bc}>\frac{ab}{bc}\) tức là \(\frac{a}{b}>\frac{a}{c}\).
suy ra điều phải chứng minh.
Đúng 0
Bình luận (0)
cho mệnh đề ∃ x ∈ R:x>x² khẳng định nào đúng A) có 1 số thực lớn hơn hoặc bằng bình phương của chính nó B)cks 1 số thực lớn hơn bình phương của nó. C) bình phương của 1 số thực lớn hơn nó. D)các số thực đề lớn hơn bình phương của nó