Cho ΔABC(A^=90o) có \(\widehat{ACB}\)B^=30o,AB=6cm
a) Tính BC
b) Vẽ tia phân giác BD của \(\widehat{ABC}\left(D\in AC\right)\) . Tính AD
Giúp e vs ạ, iu thưng nhiều:33
Cho ΔABC có \(\widehat{B}\) = 60o.
Kẻ AD và CE lần lượt là tia phân giác của \(\widehat{A}\) và \(\widehat{C}\) \(\left(D\in BC,E\in AB\right)\)
Biết BE + BD = 9 cm và chu vi tam giác ABC là 31 cm
Khi đó độ dài cạnh AC là?
Bài 1 : Cho hình thang ABCD (AB//CD), \(\widehat{A}\)=\(\widehat{D}\)=90o , AB=11cm , AD= 12 cm, Bc = 13 cm . Tính AC
Bài 2 : Cho ΔABC cân tại A. Trên cạnh AB,AC lấy điểm M,N sao cho BM = CN
a)Tứ giác BMNC là hình gì ? Vì sao ?
b)Tính các góc của tứ giác BMNC biết rằng \(\widehat{A}\) bằng 40o
Bài 2:
a) Xét ΔABC có
\(\dfrac{AM}{AB}=\dfrac{AN}{AC}\left(AM=AN;AB=AC\right)\)
Do đó: MN//BC(Định lí Ta lét đảo)
Xét tứ giác BMNC có MN//BC(gt)
nên BMNC là hình thang có hai đáy là MN và BC(Định nghĩa hình thang)
Hình thang BMNC có \(\widehat{B}=\widehat{C}\)(ΔABC cân tại A)
nên BMNC là hình thang cân(Dấu hiệu nhận biết hình thang cân)
Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Gọi BD là đường phân giác của tam giác ABC.
a) Tính độ dài DA, DC.
b) Tia phân giác của góc C cắt BD tại I. Gọi M là trung điểm của BC. Chứng minh \(\widehat{BIM}\) = 90o
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10cm
Xét ΔABC có
BD là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{DA}{AB}=\dfrac{DC}{BC}\)(Tính chất đường phân giác của tam giác)
hay \(\dfrac{DA}{6}=\dfrac{DC}{10}\)
Ta có: D nằm giữa A và C(gt)
nên DA+DC=AC
hay DA+DC=8(cm)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{DA}{6}=\dfrac{DC}{10}=\dfrac{DA+DC}{6+10}=\dfrac{8}{16}=\dfrac{1}{2}\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{DA}{6}=\dfrac{1}{2}\\\dfrac{DC}{10}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}DA=6\cdot\dfrac{1}{2}=3\left(cm\right)\\DC=10\cdot\dfrac{1}{2}=5\left(cm\right)\end{matrix}\right.\)
Vậy: DA=3cm; DC=5cm
Cho\(\Delta\) ABC vuông ở A; AB= 6cm, AC= 8cm. Vẽ đường cao AH
a, Tính BC
b, Chứng minh: \(\Delta\) ABC đồng dạng với \(\Delta\) HBA
c, Chứng minh: AB\(^2\) = BD. BC. Tính HB, HC
d, Vẽ phân giác AD của\(\widehat{BAC}\) (D\(\in\) BC). Tính DB, AD
hình bạn tự vé nhé.
tam giác ABC vuông tại A nên theo định lý PY-Ta-Go ta có:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow6^2+8^2=BC^2\)
\(\Rightarrow BC=10\left(DO-BC>0\right)\)
b) xét \(\Delta ABC\) VÀ \(\Delta HBA\) CÓ:
\(\widehat{BAC}=\widehat{AHB}\)
\(\widehat{B}\) CHUNG
\(\Rightarrow\Delta ABC\) đồng dạng vs \(\Delta HBA\)
c)sửa đề:\(AB^2=BH.BC\)
TA CÓ: \(\Delta ABC\text{ᔕ}\Delta HBA\)
\(\Rightarrow\frac{AB}{BH}=\frac{BC}{AB}\left(tsđd\right)\)
\(\Rightarrow AH^2=BH.BC\)
bạn kia làm 2 câu đầu mình làm 2 câu cuối nhé :
c, \(\Delta AHB~\Delta CAB\)
\(\Rightarrow\frac{AB}{BC}=\frac{BH}{AB}\Rightarrow AB^2=BC.BH\)
\(\Rightarrow BH=\frac{AB^2}{BC}=3,6cm\)
\(\Rightarrow HC=6,4cm\)
d, AD phân giác \(\Delta ACB\)
\(\Rightarrow\frac{DC}{DB}=\frac{AC}{AB}=\frac{8}{6}=\frac{4}{3}\)( 1 )
\(\Rightarrow DC+DB=BC=10cm\)( 2 )
Từ ( 1 ) và ( 2 ) \(\Rightarrow DB=\frac{30}{7}cm\)
AD bạn tính nốt nhé
Cho ΔABC vuông tại A, biết AB = 6cm; AC = 8cm.
a) Tính độ dài cạnh BC, so sánh \(\widehat{B}\) và \(\widehat{C}\).
b) Vẽ trung tuyến AM của ΔABC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA. Chứng minh: ΔMAB = ΔMEC và \(\widehat{ACE}\) = 90 độ.
c) Gọi H là trung điểm của cạnh AC, chứng minh: HB = HE.
d) HB cắt AE tại P, HE cắt BC tại Q, chứng minh: ΔHPQ cân.
Cho ΔABC, góc C= 90o, góc A=60o. Tia phân giác của góc BAC cắt BC tại E. Kẻ EK⊥AB ( K ∈ AB ). Kẻ BD⊥AE ( D ∈ AE ). Chứng minh rằng
a. AC=AK
b. EB>AC
c. CK // BD
a) Xét ΔACE vuông tại C và ΔAKE vuông tại K có
AE chung
\(\widehat{CAE}=\widehat{KAE}\)(AE là tia phân giác của \(\widehat{CAK}\))
Do đó: ΔACE=ΔAKE(Cạnh huyền-góc nhọn)
Suy ra: AC=AK(Hai cạnh tương ứng)
Cho ΔABC, góc A= 90o, góc B lớn hơn góc C. Vẽ phân giác giác B cắt cạnh AC tại D, vẽ DE // BC ( E ∈ AB )
a. Chứng minh: ΔBDE là tam giác cân
b. Vẽ phân giác của góc BDC cắt cạnh BC tại F, so sánh độ dài DF và CF
c. Khi cho thêm điều kiện góc C= 30o, hãy chứng minh ΔABF đều
Cho ΔABC vuông tại A có AB = 6cm, BC = 10cm và đường cao AH
a) Chứng minh: ΔABH ᔕ ΔCBA và AB2 = BH.BC
b) Tính AC, AH
c) Tia phân giác của \(\widehat{ABC}\) cắt AH, AC lần lượt tại I và D. Chứng minh: \(\dfrac{IH}{IA}\) = \(\dfrac{DA}{DC}\)
d) Tính SABI
Cho tam giác vuông ABC, góc A = 90o, góc C = 30o và đường phân giác BD (D thuộc cạnh AC).
a) Tính tỉ số AD/CD.
b) Cho biết độ dài AB = 12,5cm. Hãy tính chu vi và diện tích của tam giác ABC.
a) + Δ ABC vuông tại A, có 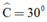
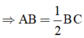
(Trong một tam giác vuông, cạnh đối diện với góc 30o bằng một nửa cạnh huyền)
+ Δ ABC có BD là phân giác của 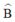
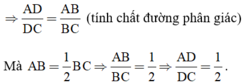
b) AB = 12,5cm ⇒ BC = 2AB = 2.12,5 = 25cm
Áp dụng định lí Py- ta- go vào tam giác ABC ta có:
AB2 + AC2 = BC2 nên AC2 = BC2 - AB2
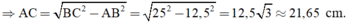
+ Chu vi tam giác ABC là:
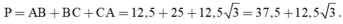
+ Diện tích tam giác ABC là:
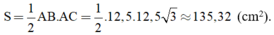
Cho \(\Delta ABC\)cân tại A (\(\widehat{B}=\widehat{C}=40^0\)). BD là tia phân giác của \(\widehat{ABC}\left(D\in AC\right)\).Trên tia AB lấy điểm M sao cho AM=BC. Chứng minh:
a) BD+AD=BC
b)Tính số đo góc AMC

a) \(\Delta ABC\)cân tại A có \(\widehat{B}=\widehat{C}\)nên \(\widehat{A}=180^0-2.40^0=100^0\)
Vẽ \(DE//BC\left(E\in AB\right)\)
Trên tia BC lấy điểm F sao cho BD = BF.
Vì BD là phân giác của \(\widehat{B}\)nên \(\widehat{ABD}=\widehat{DBC}=\frac{\widehat{B}}{2}=20^0\)
Vì \(DE//BC\)nên \(\widehat{EDB}=\widehat{DBC}\)(so le trong)
Mà \(\widehat{ABD}=\widehat{DBC}\)(Do BD là phân giác của \(\widehat{B}\))
Suy ra \(\widehat{EDB}=\widehat{ABD}\)\(\Rightarrow\Delta EBD\)tại E \(\Leftrightarrow EB=ED\)(1)
Vì \(DE//BC\)nên \(\hept{\begin{cases}\widehat{AED}=\widehat{B}\\\widehat{ADE}=\widehat{C}\end{cases}}\)(đồng vị)
Mà \(\widehat{B}=\widehat{C}\)(\(\Delta ABC\)cân tại A) nên \(\widehat{AED}=\widehat{ADE}\)
\(\Rightarrow\Delta AED\)cân tại A \(\Rightarrow AE=AD\)
Lại có AB = AC (gt) nên EB = DC (2)
Từ (1) và (2) suy ra ED = DC
BD = BF(theo cách vẽ) nên \(\Delta BDF\)cân tại B có \(\widehat{DBF}=20^0\)
\(\Rightarrow\widehat{BDF}=\widehat{BFD}=\frac{180^0-20^0}{2}=80^0\)
Mà \(\widehat{DFB}+\widehat{DFC}=180^0\)(kề bù) nên \(\widehat{DFC}=180^0-80^0=100^0\)
Áp dụng định lý về tổng ba góc trong tam giác vào tam giác FDC, có:
\(\widehat{FDC}=180^0-100^0-40^0=40^0\)
Xét \(\Delta AED\)và \(\Delta FDC\)có:
\(\widehat{ADE}=\widehat{FCD}\left(=40^0\right)\)
ED = DC( cmt)
\(\widehat{AED}=\widehat{FDC}\left(=40^0\right)\)
Suy ra \(\Delta AED=\Delta FDC\left(g-c-g\right)\)
\(\Rightarrow AD=FC\)(hai cạnh tương ứng)
Lúc đó: \(BD+AD=BF+FC=BC\left(đpcm\right)\)
b) Vẽ tam giác đều AMG trên nửa mặt phẳng bờ AB chứa điểm C
Ta có: \(\widehat{GAC}=\widehat{BAC}-\widehat{BAG}=100^0-60^0=40^0\)
Cách khác theo cô Huyền:3
Câu hỏi của thu - Toán lớp 7 - Học toán với OnlineMath
Tham khảo link này: https://olm.vn/hoi-dap/detail/84908086242.html