tìm min max y=sin3x trên [-pi/2;2pi/3]
Những câu hỏi liên quan
tìm min max của phương trình y=sin^2x-2sinx-3 trên khoảng [pi/4;2pi/3]
Xem chi tiết
bạn nên dùng hàm fx để ghi dễ nhìn hơn
Đúng 0
Bình luận (0)
Tìm max min của y=sin(x+pi/3)-sinx
\(y=sin\left(x+\dfrac{\pi}{3}\right)-sinx\)
\(=\dfrac{1}{2}sinx+\dfrac{\sqrt{3}}{2}cosx-sinx\)
\(=\dfrac{\sqrt{3}}{2}cosx-\dfrac{1}{2}sinx\)
\(=cos\left(x+\dfrac{\pi}{6}\right)\in\left[-1;1\right]\)
\(\Rightarrow\left\{{}\begin{matrix}y_{mịn}=-1\Leftrightarrow x=\dfrac{5\pi}{6}+k2\pi\\y_{max}=1\Leftrightarrow x=-\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Tìm Min, Max của : y =\(\dfrac{4}{\sqrt{2-cos\left(x-\dfrac{\pi}{6}\right)}+3}\)
ĐK: Biểu thức xác định với mọi `x`.
`y_(min) <=> (\sqrt(2-cos(x-π/6))+3)_(max) <=> (cos(x-π/6))_(max)`
`<=> cos(x-π/6)=1 <=> x-π/6=k2π <=> x = π/6+k2π ( k \in ZZ)`.
`=> y_(min) = 1`
`y_(max) <=> (\sqrt(2-cos(x-π/6))+3)_(min) <=> (cos(x-π/6))_(min)`
`<=> cos(x-π/6)=-1 <=> x -π/6= π+k2π <=> x = (7π)/6+k2π (k \in ZZ)`
`=> y_(max) = (6-2\sqrt3)/3`.
Đúng 0
Bình luận (1)
Tìm Max, Min của hàm số:1) ydfrac{x+1+sqrt{x-1}}{x+1+2sqrt{x-1}}2) ysin^{2016}x+cos^{2016}x 3) y2cos x-dfrac{4}{3}cos^3x trên left[0;dfrac{pi}{2}right]4) ysin2x-sqrt{2}x+1,xinleft[0;dfrac{pi}{2}right]5) ydfrac{4-cos^2x}{sqrt{sin^4x+1}},xinleft[-dfrac{pi}{3};dfrac{pi}{3}right]
Đọc tiếp
Tìm Max, Min của hàm số:
1) \(y=\dfrac{x+1+\sqrt{x-1}}{x+1+2\sqrt{x-1}}\)
2) \(y=\sin^{2016}x+\cos^{2016}x\)
3) \(y=2\cos x-\dfrac{4}{3}\cos^3x\) trên \(\left[0;\dfrac{\pi}{2}\right]\)
4) \(y=\sin2x-\sqrt{2}x+1,x\in\left[0;\dfrac{\pi}{2}\right]\)
5) \(y=\dfrac{4-cos^2x}{\sqrt{sin^4x+1}},x\in\left[-\dfrac{\pi}{3};\dfrac{\pi}{3}\right]\)
Tìm giá trị max, min của các hàm số sau:
1, y= 2 - \(\sin\left(\dfrac{3\pi}{2}+x\right)\cos\left(\dfrac{\pi}{2}+x\right)\)
2, y= \(\sqrt{5-2\sin^2x.\cos^2x}\)
1, \(y=2-sin\left(\dfrac{3x}{2}+x\right).cos\left(x+\dfrac{\pi}{2}\right)\)
\(y=2-\left(-cosx\right).\left(-sinx\right)\)
y = 2 - sinx.cosx
y = \(2-\dfrac{1}{2}sin2x\)
Max = 2 + \(\dfrac{1}{2}\) = 2,5
Min = \(2-\dfrac{1}{2}\) = 1,5
2, y = \(\sqrt{5-\dfrac{1}{2}sin^22x}\)
Min = \(\sqrt{5-\dfrac{1}{2}}=\dfrac{3\sqrt{2}}{2}\)
Max = \(\sqrt{5}\)
Đúng 2
Bình luận (0)
Tìm GTLN (max), GTNN (min) của hàm số
y
x
2
-
3
x
-
2
trên
5
2
;
5
Đọc tiếp
Tìm GTLN (max), GTNN (min) của hàm số y = x 2 - 3 x - 2 trên 5 2 ; 5
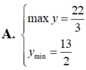
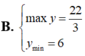
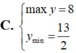
tìm min max của y = sin x trên đoạn \(\left[\frac{-\pi}{3};\frac{2\pi}{3}\right]\)
Cách lập bảng biến thiên để tìm min max ntn, chỉ rõ cách lập bảng biến thiên giúp mh đk k, cảm ơn nhé!
\(y'=cosx\) ; \(y'=0\Rightarrow cosx=0\Rightarrow x=\frac{\pi}{2}+k\pi\)
Do \(x\in\left[-\frac{\pi}{3};\frac{2\pi}{3}\right]\Rightarrow x=\frac{\pi}{2}\)
Không cần lập bảng biến thiên, chúng ta chỉ cần quan tâm 3 vị trí: 2 biên và điểm dừng vừa tìm được
\(y\left(\frac{\pi}{2}\right)=1\) ; \(y\left(-\frac{\pi}{3}\right)=-\frac{\sqrt{3}}{2}\) ; \(y\left(\frac{2\pi}{3}\right)=\frac{\sqrt{3}}{2}\)
So sánh 3 giá trị trên ta được:
\(y_{max}=1\) khi \(x=\frac{\pi}{2}\)
\(y_{min}=-\frac{\sqrt{3}}{2}\) khi \(x=-\frac{\pi}{3}\)
Đúng 0
Bình luận (0)
Tìm min, max của hàm số: y= \(\frac{\pi}{4}\)+ sin2x
Tìm max-min của hs y=4sin²x+√2sin(2x+pi/4)