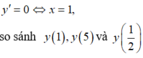tìm min, max của y=4sin2x+2cos2x

Những câu hỏi liên quan
tìm min và max của hàm số:
\(y=sinx\left(1-2cos2x\right)\)
Hình như lớp 11 học đạo hàm rồi thì phải
\(y=sinx\left(1-2\left(1-2sin^2x\right)\right)=sinx\left(4sin^2x-1\right)=4sin^3x-sinx\)
Xét hàm \(f\left(t\right)=4t^3-t\) với \(t\in\left[-1;1\right]\)
\(f'\left(t\right)=12t^2-1=0\Rightarrow\left[{}\begin{matrix}t=\frac{\sqrt{3}}{6}\\t=\frac{-\sqrt{3}}{6}\end{matrix}\right.\)
Ta có: \(f\left(-1\right)=-3;f\left(1\right)=3;f\left(\frac{\sqrt{3}}{6}\right)=\frac{-\sqrt{3}}{9};f\left(\frac{-\sqrt{3}}{6}\right)=\frac{\sqrt{3}}{9}\)
\(\Rightarrow y_{min}=-3\) khi \(sinx=-1\Rightarrow x=-\frac{\pi}{2}+k2\pi\)
\(y_{max}=3\) khi \(sinx=1\Rightarrow x=\frac{\pi}{2}+k2\pi\)
Đúng 0
Bình luận (0)
Tìm m để pt có 2 nghiệm thuộc \(\left[\dfrac{-\pi}{2};\dfrac{\pi}{2}\right]\)
(2cosx-1)(2cos2x+2cosx-m)= 3-4sin2x
Giải phương trình sau: 2cos2x - 3√3sin2x - 4sin2x = -4
Phương trình
2
cos
2
x
-
3
3
sin
2
x
-
4
sin
2
x
-
4
có họ nghiệm là
Đọc tiếp
Phương trình 2 cos 2 x - 3 3 sin 2 x - 4 sin 2 x = - 4 có họ nghiệm là
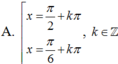
![]()
![]()
![]()
Hướng dẫn giải:
Chọn A.
+ Trường hợp 1.
![]() : là nghiệm của phương trình
: là nghiệm của phương trình
+ Trường hợp 2.
![]() : Chia 2 vế phương trình cho cos2x ta được
: Chia 2 vế phương trình cho cos2x ta được
![]()
![]()
Đúng 0
Bình luận (0)
Câu 1 : Chứng minh rằng : 3 - 4sin2x = 4cos2x - 1Câu 2 : Chứng minh rằng : cos4x - sin4x = 2cos2x - 1 = 1 - 2sin2xCâu 3 : Chứng minh rằng : sin4x + cos4x = 1 - 2sin2xCos2x
1/ \(3-4\sin^2=4\cos^2x-1\Leftrightarrow4\left(\sin^2x+\cos^2x\right)-4=0\Leftrightarrow4.1-4=0\left(ld\right)\Rightarrow dpcm\)
2/ \(\cos^4x-\sin^4x=\left(\cos^2x+\sin^2x\right)\left(\cos^2x-\sin^2x\right)=\cos^2x-\left(1-\cos^2x\right)=2\cos^2x-1=\left(1-\sin^2x\right)-\sin^2x=1-2\sin^2x\)
3/ \(\sin^4x+\cos^4x=\left(\sin^2x+\cos^2x\right)^2-2\sin^2x.\cos^2x=1-2\sin^2x.\cos^2x\)
Đúng 2
Bình luận (0)
Tìm Min,Max của các hàm số
a/ y= 2sin bình x+ cos bình 2x+2
b/ y=4sin2x + 5cos2x -2
c/ y= 3sin(2x-(pi/3))-2cos(2x-(pi/3))+1
d/ y=(2sin bình 3x+4sin3x.cos3x+1)/(sin6x+4cos6x+10)
Giusp mình với ạ!!! Thực sự mình rất cầN!!! Mình cảm ơn!
tìm min max của của I x + y I ≤ 2
\(\Leftrightarrow-2\le x+y\le2\\ Max\Leftrightarrow x=2-y\\ Min\Leftrightarrow x=-2-y\)
Đúng 1
Bình luận (0)
1, cho x, y thay đổi thỏa mãn: x^2+y^2=2
tìm min max của P=2(x^3+y^3)-3xy
2, cho x, y thay đổi thỏa mãn x^2+y^2=1
tìm min max của P=( 2x^2+12xy)/ (1+2xy+2y^2)
1. Đặt x = √2.cosα và y = √2.sinα (với α trên [0,3π/2])
Ta có: P = 4√2(sinα + cosα)(1 - sinαcosα) - 6sinαcosα
Đặt t = sinα + cosα = √2.sin(α + π/4) có |t| ≤ √2, nên sinαcosα = (t^2 - 1)/2
suy ra P = -2√2.t^3 - 3t^2 + 6√2.t + 3.
Đến đây bạn áp dụng P' = 0 rồi xét các gtrị cực trị.
2. Đặt x = cosα và y = sinα (với α trên [0,3π/2])
Biến đổi P = (6sin2α + cos2α + 1) / (3 + sin 2α - cos 2α)
Mặt khác lại có (cos2α)^2 + (sin 2α)^2 = 1.
Ta áp dụng P' = 0 tiếp.
Đúng 0
Bình luận (0)
Tìm max min của y=sin(x+pi/3)-sinx
\(y=sin\left(x+\dfrac{\pi}{3}\right)-sinx\)
\(=\dfrac{1}{2}sinx+\dfrac{\sqrt{3}}{2}cosx-sinx\)
\(=\dfrac{\sqrt{3}}{2}cosx-\dfrac{1}{2}sinx\)
\(=cos\left(x+\dfrac{\pi}{6}\right)\in\left[-1;1\right]\)
\(\Rightarrow\left\{{}\begin{matrix}y_{mịn}=-1\Leftrightarrow x=\dfrac{5\pi}{6}+k2\pi\\y_{max}=1\Leftrightarrow x=-\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Tìm GTLN (max), GTNN (min) của
y
2
x
-
1
+
4
5
-
x
Đọc tiếp
Tìm GTLN (max), GTNN (min) của y = 2 x - 1 + 4 5 - x
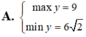
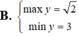
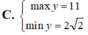
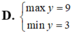








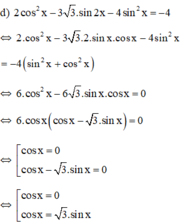
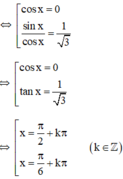
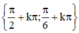 (k ∈ Z)
(k ∈ Z)