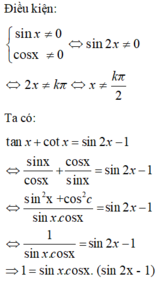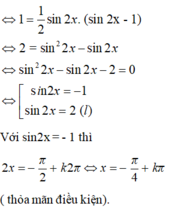\(cotx-tanx+4sin2x=\frac{2}{sin2x}\)

Những câu hỏi liên quan
Giải phương trình cotx - tanx + 4sin2x = 2/sin2x
Đối với những phương trình lượng giác chứa tanx, cotx, sin2x hoặc cos2x, ta có thể đưa về phương trình chứa cosx, sinx, sin2x, hoặc cos2x ngoài ra cũng có thể đặt ẩn phụ t = tanx để đưa về một phương trình theo t.
Cách 1: Điều kiện của phương trình:
sin2x ≠ 0 ⇔ cos2x ≠ 1 hoặc cos2x ≠ -1 (1)
Ta có:
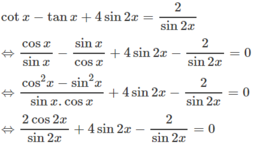
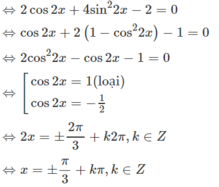
Cách 2. Đặt t = tanx
Điều kiện t ≠ 0
Phương trình đã cho có dạng
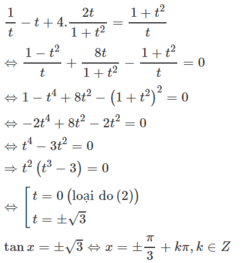
Đúng 0
Bình luận (0)
\(cotx-1=\frac{cos2x}{1+tanx}+sin^2x-\frac{1}{2}sin2x\)
ĐKXĐ: \(\left\{{}\begin{matrix}sin2x\ne0\\tanx\ne-1\end{matrix}\right.\)
\(\frac{cosx}{sinx}-1=\frac{cos^2x-sin^2x}{1+\frac{sinx}{cosx}}+sin^2x-sinx.cosx\)
\(\Leftrightarrow\frac{cosx-sinx}{sinx}=cosx\left(cosx-sinx\right)-sinx\left(cosx-sinx\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx-sinx=0\Rightarrow x=\frac{\pi}{4}+k\pi\\\frac{1}{sinx}=cosx-sinx\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow sinx.cosx-sin^2x=1\)
\(\Leftrightarrow2sinx.cosx+1-2sin^2x=3\)
\(\Leftrightarrow sin2x+cos2x=3\)
Vế trái không lớn hơn 2 nên pt vô nghiệm
Đúng 0
Bình luận (0)
sin2x/tanx+cotx x (tanx+cotx)=2sin2x
giúp vs ạ gấp lắm ạ
Để giải phương trình sin2x/tanx+cotx * (tanx+cotx) = 2sin2x, ta có thể sử dụng các quy tắc và công thức trong giải tích. Đầu tiên, ta có thể thay thế các hàm lượng giác bằng các công thức tương đương. Sau đó, ta có thể rút gọn và giải phương trình.
Đúng 0
Bình luận (0)
1.Giải các pt sau
a) tan2x + cotx = 8cos2x
b) cotx - tanx + 4sin2x = 2 / sin2x ( dấu chia nha )
c) 5 sinx - 2 = 3(1 - sinx)tan2x
2.Tìm tham số m để pt có nghiệm
a) (m + 1)sin2x - sin2x + cos2x = 0
b) 2sin2x + msin2x = 2m
c) Nghiệm thuộc khoảng [0:π/4] sin2x - 4sinxcox + (m-2)cos2x = 0
ĐKXĐ: ...
a/ \(\frac{sin2x}{cos2x}+\frac{cosx}{sinx}=8cos^2x\)
\(\Leftrightarrow sin2x.sinx+cos2x.cosx=8cos^2x.sinx.cos2x\)
\(\Leftrightarrow cosx=4sin2x.cos2x.cosx\)
\(\Leftrightarrow cosx=2sin4x.cosx\)
\(\Leftrightarrow cosx\left(2sin4x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\sin4x=\frac{1}{2}\end{matrix}\right.\) \(\Leftrightarrow...\)
b/ \(\frac{cosx}{sinx}-\frac{sinx}{cosx}+4sin2x=\frac{1}{sinx.cosx}\)
\(\Leftrightarrow cos^2x-sin^2x+4sin2x.sinx.cosx=1\)
\(\Leftrightarrow cos2x+2sin^22x=1\)
\(\Leftrightarrow cos2x+2\left(1-cos^22x\right)=1\)
\(\Leftrightarrow-2cos^22x+cos2x+1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=1\\cos2x=-\frac{1}{2}\end{matrix}\right.\) \(\Leftrightarrow...\)
1c/
\(5sinx-2=3\left(1-sinx\right)\frac{sin^2x}{1-sin^2x}\)
\(\Leftrightarrow5sinx-2=\frac{3sin^2x}{1+sinx}\)
\(\Leftrightarrow\left(5sinx-2\right)\left(1+sinx\right)=3sin^2x\)
\(\Leftrightarrow5sin^2x+3sinx-2=3sin^2x\)
\(\Leftrightarrow2sin^2x+3sinx-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\frac{1}{2}\\sinx=-2\left(l\right)\end{matrix}\right.\) \(\Rightarrow x=...\)
Bài 2:
a/ \(\Leftrightarrow\frac{\left(m+1\right)\left(1-cos2x\right)}{2}-sin2x+cos2x=0\)
\(\Leftrightarrow2sin2x+\left(m-1\right)cos2x=m+1\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(4+\left(m-1\right)^2\ge\left(m+1\right)^2\)
\(\Leftrightarrow4m\le4\Rightarrow m\le1\)
Bài 2:
b/ \(\Leftrightarrow1-cos2x+msin2x=2m\)
\(\Leftrightarrow msin2x-cos2x=2m-1\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(m^2+1\ge\left(2m-1\right)^2\)
\(\Leftrightarrow3m^2-4m\le0\)
\(\Rightarrow0\le m\le\frac{4}{3}\)
c/ Với \(cosx=0\) không phải là nghiệm
Với \(cosx\ne0\), chia 2 vế cho \(cos^2x\) ta được:
\(tan^2x-4tanx+m-2=0\)
Đặt \(tanx=t\Rightarrow t\in\left[0;1\right]\)
Phương trình trở thành: \(t^2-4t+m-2=0\)
\(\Leftrightarrow f\left(t\right)=t^2-4t-2=-m\)
Dựa vào đồ thị hàm \(f\left(t\right)=t^2-4t-2\), để \(y=-m\) cắt \(y=f\left(t\right)\) với \(t\in\left[0;1\right]\) \(\Rightarrow-5\le-m\le-2\)
\(\Rightarrow2\le m\le5\)
giải các pt
a) \(4sin^3x+3\sqrt{2}sin2x=8sinx\)
b) \(7cosx=4cos^3x+4sin2x\)
c) \(tanx+cotx=5-\frac{3}{sin^22x}\)
d) \(5\left(1+cosx\right)=2+sin^4x-cos^4x\)
e) \(2\left(cos^2x+cos^22x+cos^23x\right)=3\left(1+cosx.cos4x\right)\)
a/
\(\Leftrightarrow4sin^3x+6\sqrt{2}sinx.cosx-8sinx=0\)
\(\Leftrightarrow2sinx\left(2sin^2x+3\sqrt{2}cosx-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\Rightarrow x=k\pi\\2sin^2x+3\sqrt{2}cosx-4=0\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow2\left(1-cos^2x\right)+3\sqrt{2}cosx-4=0\)
\(\Leftrightarrow-2cos^2x+3\sqrt{2}cosx-2=0\)
\(\Rightarrow\left[{}\begin{matrix}cosx=\sqrt{2}>1\left(l\right)\\cosx=\frac{\sqrt{2}}{2}\end{matrix}\right.\)
\(\Rightarrow x=\pm\frac{\pi}{4}+k2\pi\)
Đúng 0
Bình luận (0)
b/
\(\Leftrightarrow4cos^3x+8sinx.cosx-7cosx=0\)
\(\Leftrightarrow cosx\left(4cos^2x+8sinx-7\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}cosx=0\Rightarrow x=\frac{\pi}{2}+k\pi\\4cos^2x+8sinx-7=0\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow4\left(1-sin^2x\right)+8sinx-7=0\)
\(\Leftrightarrow-4sin^2x+8sinx-3=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=\frac{3}{2}\left(l\right)\\sinx=\frac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+k2\pi\\x=\frac{5\pi}{6}+k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
c/
ĐKXĐ; ...
\(\Leftrightarrow\frac{sinx}{cosx}+\frac{cosx}{sinx}-5+\frac{3}{sin^22x}=0\)
\(\Leftrightarrow\frac{sin^2x+cos^2x}{sinx.cosx}-5+\frac{3}{sin^22x}=0\)
\(\Leftrightarrow\frac{3}{sin^22x}+\frac{2}{sin2x}-5=0\)
Đặt \(\frac{1}{sin2x}=t\Rightarrow3t^2+2t-5=0\)
\(\Rightarrow\left[{}\begin{matrix}t=1\\t=-\frac{5}{3}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\frac{1}{sin2x}=1\\\frac{1}{sin2x}=-\frac{5}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}sin2x=1\\sin2x=-\frac{3}{5}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+k\pi\\x=\frac{1}{2}arcsin\left(-\frac{3}{5}\right)+k\pi\\x=\frac{\pi}{2}-\frac{1}{2}arcsin\left(-\frac{3}{5}\right)+k\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Nghiệm của phương trình
tan
x
+
c
o
t
x
sin
2
x
–
1
là: A.
x
π
4
+
k
2
π
,
k
∈
ℤ
B.
x
-
π
4
+
k
π
,
k
∈
ℤ...
Đọc tiếp
Nghiệm của phương trình tan x + c o t x = sin 2 x – 1 là:
A. x = π 4 + k 2 π , k ∈ ℤ
B. x = - π 4 + k π , k ∈ ℤ
C. x = - π 4 + k 2 π , k ∈ ℤ
D. x = π 4 + k π , k ∈ ℤ
Giải phương trình
c
o
t
x
-
1
cos
2
x
1
+
tan
x
+
sin
2
x
-
1
2
sin...
Đọc tiếp
Giải phương trình c o t x - 1 = cos 2 x 1 + tan x + sin 2 x - 1 2 sin 2 x
Điều kiện của phương trình: sinx ≠ 0, cos ≠ 0, tan ≠ -1.
Biến đổi tương đương đã cho, ta được
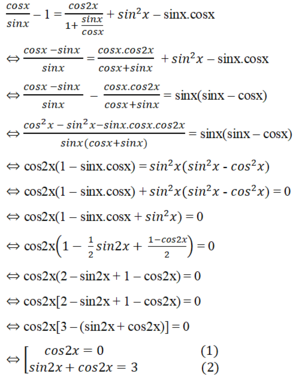
Phương trình (2) vô nghiệm vì |sin2x + cos2x| ≥ √2.
Phương trình (1) có nghiệm 2x = π/2+kπ,k ∈ Z
⇒ x = π/4+ k π/2,k ∈ Z.
Giá trị x = π/4+ k π/2, k = 2n + 1,
với n ∈ Z bị loại do điều kiện tanx ≠ -1.
Đúng 0
Bình luận (0)
giải phương trình: sin^4x+cos^4x/sin2x=1/2(tanx+cotX)
giai pt:
a) \(\left(2cosx-1\right)\left(2sinx+cosx\right)=sin2x-sinx\)
b) \(\frac{sin2x}{cosx}+\frac{cos2x}{sinx}=tanx-cotx\)
c) \(\frac{1}{cos^2x}=\frac{2-sin^3x-cos^2x}{1-sin^3x}\)
a/
\(\Leftrightarrow\left(2cosx-1\right)\left(2sinx+cosx\right)=2sinx.cosx-sinx\)
\(\Leftrightarrow\left(2cosx-1\right)\left(2sinx+cosx\right)-sinx\left(2cosx-1\right)=0\)
\(\Leftrightarrow\left(2cosx-1\right)\left(2sinx+cosx-sinx\right)=0\)
\(\Leftrightarrow\left(2cosx-1\right)\left(sinx+cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2cosx-1=0\\sinx+cosx=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=\frac{1}{2}\\sin\left(x+\frac{\pi}{4}\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\pm\frac{\pi}{3}+k2\pi\\x=-\frac{\pi}{4}+k\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
b/ ĐKXĐ: \(x\ne\frac{k\pi}{2}\)
\(\Leftrightarrow\frac{sin2x.sinx+cos2x.cosx}{sinx.cosx}=\frac{sinx}{cosx}-\frac{cosx}{sinx}\)
\(\Leftrightarrow\frac{cos\left(2x-x\right)}{sinx.cosx}=\frac{sin^2x-cos^2x}{sinx.cosx}\)
\(\Leftrightarrow cosx=sin^2x-cos^2x\)
\(\Leftrightarrow cosx=1-2cos^2x\)
\(\Leftrightarrow2cos^2x+cosx-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=-1\left(l\right)\\cosx=\frac{1}{2}\end{matrix}\right.\)
\(\Rightarrow x=\pm\frac{\pi}{3}+k2\pi\)
Đúng 0
Bình luận (0)
c/ ĐKXĐ: \(x\ne\frac{\pi}{2}+k\pi\)
\(\Leftrightarrow\frac{1}{cos^2x}=\frac{1-cos^2x+1-sin^3x}{1-sin^3x}\)
\(\Leftrightarrow\frac{1}{cos^2x}=\frac{sin^2x}{1-sin^3x}+1\)
\(\Leftrightarrow\frac{1}{cos^2x}-1=\frac{sin^2x}{1-sin^3x}\)
\(\Leftrightarrow\frac{1-cos^2x}{cos^2x}=\frac{sin^2x}{1-sin^3x}\)
\(\Leftrightarrow\frac{sin^2x}{cos^2x}=\frac{sin^2x}{1-sin^3x}\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\Rightarrow x=k\pi\\cos^2x=1-sin^3x\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow1-sin^2x=1-sin^3x\)
\(\Leftrightarrow sin^3x-sin^2x=0\Leftrightarrow\left[{}\begin{matrix}sinx=0\\sinx=1\left(l\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)