\(=\left(x-y\right)\left(x+y\right)-10\left(x+y\right)=\)

\(=\left(x+y\right)\left(x-y-10\right)\)

= (x - y). (x + y) - 10 ( x - y)

= [( x + y) - 10)] . ( x - y)

  \(x^2\) - y² - 10\(x\) - 10y 

= (\(x^2\) - y²) - 10.(\(x\) + y)

= (\(x-y\))(\(x\) + y) - 10.(\(x\) + y)

= (\(x\) + y).(\(x\) - y - 10)

Đây nè bạn.

a) Ta có: \(M=x^2-2xy+y^2-10x+10y\)

\(=\left(x-y\right)^2-10\left(x-y\right)\)

\(=9^2-10\cdot9=-9\)

Ta có: \(4\ge2\left(x^2+y^2\right)\ge\left(x+y\right)^2\)

    \(\Rightarrow x+y\le2\)

Ta có: \(P=\sqrt{x\left(14x+10y\right)}+\sqrt{y\left(14y+10x\right)}\)

              \(=\sqrt{\dfrac{24x\left(14x+10y\right)}{24}}+\sqrt{\dfrac{24y\left(14y+10x\right)}{24}}\le\dfrac{\dfrac{24x+14x+10y}{2}}{\sqrt{24}}+\dfrac{\dfrac{24y+14y+10x}{2}}{\sqrt{24}}\)

\(\Leftrightarrow P\le\dfrac{24\left(x+y\right)}{2\sqrt{6}}\le\dfrac{24.2}{2\sqrt{6}}=4\sqrt{6}\)

Dấu "=" xảy ra ⇔ x = y = 1

Ta có hệ số a= 5; b= 0 và c= -11 nên bán kính là R= a 2 + b 2 - c = 6

Chọn A.

Đáp án: A

Ta có:

(C): x 2  + y 2  - 8x + 10y + 2m - 1 = 0 ⇔ (x - 4 ) 2  + (y + 5 ) 2  = 42 - 2m

Để (C) là phương trình đường tròn thì 42 - 2m > 0 ⇔ m < 21

Ta có: đường tròn: x²+ y²- 10x + 1= 0 => (x- 5)² + y²= 24 có tâm I(5;0) .Khoảng cách từ I đến Oy là  d ( I ;   O y   ) = 5

_{Chọn D.}

Ta có hệ số a= 4; b= -5 và c= m.

Để C là đường tròn có bán kính R= 7 thì:

R = 4 2 + 5 2 - m = 7   ⇔ m = - 8

Chọn C.

Chọn A

Đáp án A.

Phương trình mặt cầu (S) có tâm O(a,b,c) bán kính R  là:

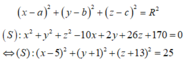
Suy ra tọa độ tâm mặt cầu là (5; -1; -13)