a.

\(\Leftrightarrow m-cosx\ge0\) ; \(\forall x\)

\(\Leftrightarrow m\ge max\left(cosx\right)\)

\(\Leftrightarrow m\ge1\)

b.

\(\Leftrightarrow2sinx-m\ge0\) ; \(\forall x\)

\(\Leftrightarrow m\le2sinx\) ; \(\forall x\)

\(\Leftrightarrow m\le\min\limits_{x\in R}\left(2sinx\right)\)

\(\Leftrightarrow m\le-2\)

c.

\(\Leftrightarrow cosx+m\ne0\) ; \(\forall x\)

\(\Leftrightarrow\left[{}\begin{matrix}m>\max\limits_R\left(cosx\right)\\m< \min\limits_R\left(cosx\right)\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\)

1. Không dịch được đề

2.

\(-1\le cos2x\le1\Rightarrow1\le y\le3\)

3.

a. \(-2\le2sinx\le2\Rightarrow-1\le y\le3\)

\(y_{min}=-1\) khi \(sinx=-1\Rightarrow x=-\dfrac{\pi}{2}+k2\pi\)

\(y_{max}=3\) khi \(sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)

b.

\(0\le cos^2x\le1\Rightarrow-1\le y\le2\)

\(y_{min}=-1\) khi \(cos^2x=1\Rightarrow x=k\pi\)

\(y_{max}=2\) khi \(cosx=0\Rightarrow x=\dfrac{\pi}{2}+k\pi\)

4.

\(y=\left(tanx-1\right)^2+2\ge2\)

\(y_{min}=2\) khi \(tanx=1\Rightarrow x=\dfrac{\pi}{4}+k\pi\)

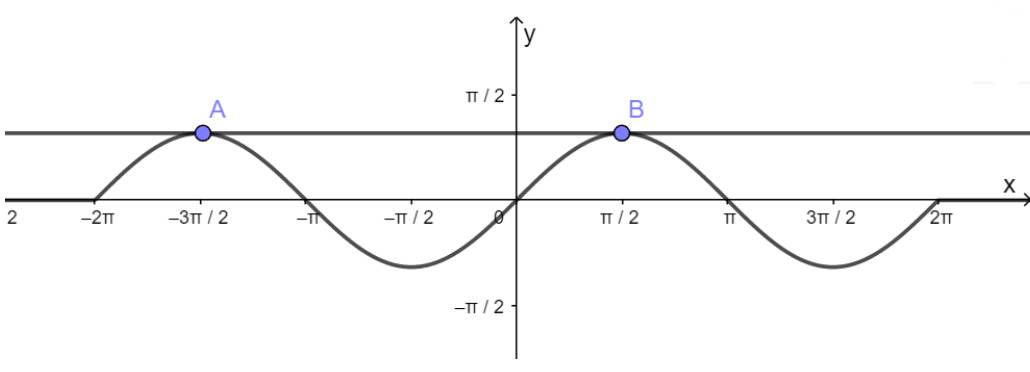
a)     Hàm số y = sinx nhận giá trị bằng 1

-        Vẽ hàm số y = sinx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)

-        Vẽ hàm số y = 1

-        Lấy giao điểm của hai hàm số y = sinx và y = 1 là A, B,...

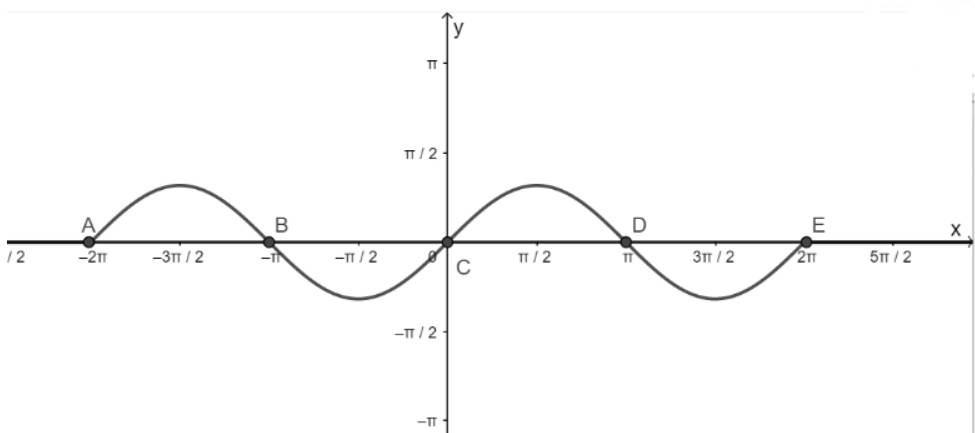
b)     Hàm số y = sinx nhận giá trị bằng 0

-        Vẽ hàm số y = sinx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)

-        Vẽ hàm số y = 0

-        Lấy giao điểm của hai hàm số y = sinx và y = 0 là A, B, C, D, E,...

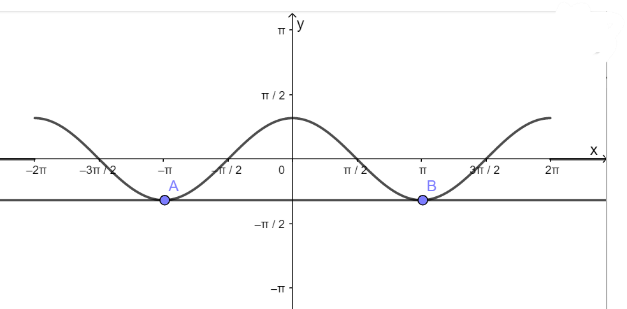
c)     Hàm số y = cosx nhận giá trị bằng – 1

-        Vẽ hàm số y = cosx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)

-        Vẽ hàm số y = - 1

-        Lấy giao điểm của hai hàm số y = cosx và y = - 1 là A, B,...

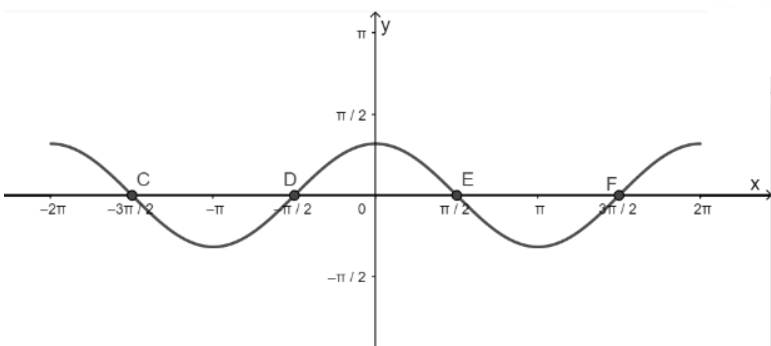
d)     Hàm số y = cosx nhận giá trị bằng 0

-        Vẽ hàm số y = cosx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)

-        Vẽ hàm số y = 0

-        Lấy giao điểm của hai hàm số y = cosx và y = 0 là C, D, E, F,...

\(\Leftrightarrow y\left(sinx+2cosx+4\right)=2sinx+cosx\)

\(\Leftrightarrow sinx\left(y-2\right)+cosx\left(2y-1\right)+4=0\) 

\(y=\sqrt{\left(sinx+cosx\right)^2+2\cdot sinx\cdot cosx+2}\)

\(=\sqrt{1+2sinx\cdot cosx+2\cdot sinx\cdot cosx+2}\)

\(=\sqrt{3+2sin2x}\)

\(-1< =sin2x< =1\)

=>\(-2< =2\cdot sin2x< =2\)

=>\(-2+3< =2\cdot sin2x+3< =5\)

=>\(1< =2\cdot sin2x+3< =5\)

=>\(1< =\sqrt{2\cdot sin2x+3}< =\sqrt{5}\)

=>\(1< =y< =\sqrt{5}\)

\(y_{min}=1\) khi \(sin2x=-1\)

=>\(2x=-\dfrac{\Omega}{2}+k2\Omega\)

=>\(x=-\dfrac{\Omega}{4}+k\Omega\)

\(y_{max}=\sqrt{5}\) khi sin 2x=1

=>\(2x=\dfrac{\Omega}{2}+k2\Omega\)

=>\(x=\dfrac{\Omega}{4}+k\Omega\)

1: ĐKXĐ: 3-cosx>0

=>cosx<3(luôn đúng)

2: ĐKXĐ: 1-sin 3x>=0

=>sin 3x<=1(luôn đúng)

3: ĐKXĐ: sin x<>0 và 2x<>pi/2+kpi

=>x<>kpi và x<>pi/4+kpi/2

4: ĐKXĐ: 2x-1>=0

=>x>=1/2

\(\Leftrightarrow\left(2m-1\right)sinx-\left(m+2\right)cosx+4m-3\ge0\) ;\(\forall x\)

\(\Leftrightarrow m\ge\dfrac{sinx+2cosx+3}{2sinx-cosx+4}=P\)

\(\Leftrightarrow m\ge P_{max}\)

Ta có: \(P=\dfrac{sinx+2cosx+3}{2sinx-cosx+4}\Leftrightarrow\left(2P-1\right)sinx-\left(P+2\right)cosx=3-4P\)

Theo điều kiện có nghiệm của pt lượng giác bậc nhất:

\(\left(2P-1\right)^2+\left(P+2\right)^2\ge\left(3-4P\right)^2\)

\(\Leftrightarrow11P^2-24P+4\le0\)

\(\Rightarrow\dfrac{2}{11}\le P\le2\)

\(\Rightarrow m\ge2\)