Câu 14 : Cho tam giác nhọn ABC có AB < AC . Kẻ AH vuông góc với BC ( H thuộc AC ) , AE là tia phân giác góc HAC . Kẻ ED vuông góc vớii AC ( D thuộc AC ) . Chứng minh rằng :
a, Tam giác HAE = tam giác DAE
b, EC > HE
Cho tam giác nhọn ABC có AB<AC .kẻ AH vuông góc với BC (H thuộc BC),AE là tia phân giác góc HAC.kẻ ED vuông góc với AC (D thuộc AC) CMR:a,Tam giác AHE=tam giác ADE;b,Tam giác AHD CÂn;c,EC>HE
a, Xét tam giác AHE và tam giác ADE:
góc HAE=góc DAE(phân giác AE)
AE(cạnh chung)
góc AHE= góc ADE(=90 độ)
\(\Leftrightarrow\)tam giác AHE = Tam giác ADE(cạnh huyền-góc nhọn)
b, Tam giác AHD:
AH=AD(cặp cạnh tương ứng)
\(\Rightarrow\)\(\Delta\)AHD cân tại A
c, \(\Delta\)vuông DEC:
EC>DE(cạnh huyền>cạnh góc vuông)
mà HE=DE(cặp cạnh tương ứng)
\(\Leftrightarrow\)EC>HE
Cho tam giac ABC vuông tại A có AB = 6cm, AC = 8cm. Kẻ đường cao AH sao cho AH vuông góc với BC (H thuộc BC) a. Tính độ dài BC b. Tia phân giác góc HAC cắt cạnh BC tại D. Qua D kẻ DK vuông góc AC (K thuộc AC). Chứng minh tam giác AHD = AKD c. Chứng minh tam giác BAD cân d. Tia phân giác góc BAH cắt canh BC tại E. Chứng minh: AB + AC = BC + DE
câu d ai giúp vớiCho tam giác ABC vuông tại A có AB < AC .Kẻ AH vuông góc với BC ,AD là phân giác của góc HAC (D thuộc cạnh BC ). từ D kẻ DE vuông góc với AC. Đường thẳng AH cắt đường thẳng ED tại M
a)chứng minh tam giác AHD = tam giác AED rồi suy ra BH = DE
b) Chứng minh tam giác BMC cân
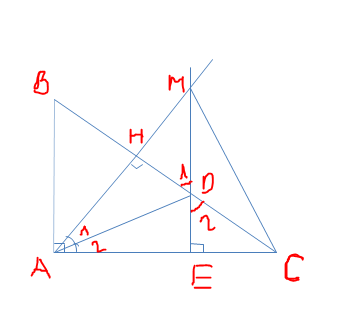
a/ Xét \(\Delta\) vuông AHD và \(\Delta\) AED. Có:
\(\widehat{A1}\)= \(\widehat{A2}\) ( giả thiết)
AD chung
=> \(\Delta AHD=\Delta AED\) ( ch-gn)
=> DH = DE ( 2 cạnh tương ứng )
b/ BMC không cân được bạn nhé. bạn chép nhầm đề bài r: Chứng minh DMC cân mới đúng.
Xét \(\Delta vuôngHDM\) và \(\Delta vuôngEDC\). Có:
\(\widehat{D1}\) = \(\widehat{D2}\) ( đối đỉnh)
HD = HE ( cmt)
=> \(\Delta HDM=\Delta EDC\left(cgv-gnk\right)\)
=> DM = DC ( 2 cạnh tương ứng)
=> Xét \(\Delta DMCcóDM=DC=>\Delta DMCcân\left(cântạiD\right)\)
~ Cậu ktra lại nhé~
Cho tam giác ABC vuông tại A có AB = 5cm , AC = 12cm . Kẻ đường cao AH ( H thuộc BC).
a) Tính độ dài cạnh BC
b) Tia phân giác của góc HAC cắt cạnh BC tại D. Qua D kẻ DK vuông góc với AC ( K thuộc AC ). Chứng minh tam giác AHD = tam giác AKD
c) Chứng minh tam giác BAD cân
d) Tia phân giác của góc BAH cắt BC tại E. Chứng minh AB + AC = BC + DE
giúp mình với ạ , tầm 30 phút nữa mình phải kt bài này rồi :(
Cho tam giác ABC vuông tại A có AB = 5cm , AC = 12cm . Kẻ đường cao AH ( H thuộc BC)
a) Tính độ dài cạnh BC
b) Tia phân giác của góc HAC cắt cạnh BC qua D. Qua D kẻ DK vuông góc với AC ( K thuộc AC ). Chứng minh rằng tam giác AHD = tam giác AKD
c) Chứng minh tam giác BAD cân
d) Tia phân giác của góc BAH cắt BC tại E. Chứng minh AB+AC = BC + DE
a) Xét \(\Delta ABC\)có AB = 5cm; AC = 12cm. Theo định lý Py-ta-go ta có:
\(BC^2=AB^2+AC^2\)
\(BC^2=5^2+12^2\)
\(BC^2=25+144\)
\(BC^2=169\)
\(BC=13\)
Vậy cạnh BC = 13cm
b)Xét tam giác AHD và tam giác AKD ta có:
\(\widehat{AHD}=\widehat{AKD}=90^o\)
AD chung
\(\widehat{DAH}=\widehat{DAK}\)(AD là tia phân giác)
=> tam giác AHD = tam giác AKD (g.c.g)
Cho tam giác ABC vuông tại A có AB=6cm,AC=8cm. Kẻ đường cao AH vuông góc với BC (H thuộc BC).
a) Tính độ dài BC.
b) Tia phản giác góc HAC cắt cạnh BC tại D. Qua D kẻ DK vuông góc với AC (K thuộc AC). Chứng minh: tam giác AHD = tam giác AKD.
c) Chứng minh: tam giác BAD cân.
d) Tia phân giác góc BAH cắt cạnh BC tại E. Chứng minh: AB+AC=BC+DE.
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Vậy: BC=10cm
b) Xét ΔAHD vuông tại H và ΔAKD vuông tại K có
AD chung
\(\widehat{HAD}=\widehat{KAD}\)(AD là tia phân giác của \(\widehat{HAK}\))
Do đó: ΔAHD=ΔAKD(cạnh huyền-góc nhọn)
c) Ta có: ΔADH vuông tại H(gt)
nên \(\widehat{HDA}+\widehat{HAD}=90^0\)(hai góc nhọn phụ nhau)
hay \(\widehat{BDA}+\widehat{HAD}=90^0\)(2)
Ta có: \(\widehat{BAD}+\widehat{CAD}=\widehat{BAC}\)(tia AD nằm giữa hai tia AB,AC)
nên \(\widehat{BAD}+\widehat{KAD}=90^0\)(3)
Từ (2) và (3) suy ra \(\widehat{BDA}=\widehat{BAD}\)
Xét ΔBAD có \(\widehat{BDA}=\widehat{BAD}\)(cmt)
nên ΔBAD cân tại B(Định lí đảo của tam giác cân)
Cho tam giác ABC cân có AB=AC=5cm, BC= 8cm . Kẻ AH vuông góc với BC tại H.
a) chứng minh: AH là tia phân giác của A.
b) Tính độ dài AH.
c) Kẻ HD vuông góc với AB ( D thuộc AB), Kẻ HE vuông góc với AC ( E thuộc AC) chứng minh tam giác HDE là tam giác cân.
có vẽ hình ạ
a) Xét tam giác ABC cân tại A: AH là đường cao (AH vuông góc với BC).
=> AH là đường phân giác góc A (Tính chất tam giác cân).
b) Xét tam giác ABC cân tại A: AH là đường cao (AH vuông góc với BC).
=> AH là đường trung tuyến (Tính chất tam giác cân).
=> H là trung điểm của BC.
=> BH = HC = \(\dfrac{1}{2}\) BC = \(\dfrac{1}{2}\).8 = 4 (cm).
Xét tam giác AHB vuông tại A:
Ta có: \(AB^2=AH^2+BH^2H^2\) (Định lý Pytago).
=> \(5^2=AH^2+4^2.\) => \(AH^2=5^2-4^2=9.\)
=> AH = 3 (cm).
c) Xét tam giác AHD vuông tại D và tam giác AHE vuông tại A:
AH chung.
Góc DAH = Góc EAH (AH là đường phân giác góc A).
=> Tam giác AHD = Tam giác AHE (ch - gn).
=> HD = HE (2 cạnh tương ứng).
=> Tam giác DHE cân tại H.
Cho tam giác ABC vuông tại A, phân giác BD. Từ D kẻ DE vuông góc với BC (E thuộc BC)
a. Chứng minh tam giác ABD= tam giác EBD
b. Chứng minh DB là trung trực của AE
c. Kẻ AH vuông góc BC (H thuộc BC), kẻ EK vuông góc AC (K thuộc AC). Chứng minh tam giác AHE = tam giác AKE
d. Chứng minh AB+AC < BC + AH
1.Cho tam giác ABC có AB=3cm,AC=4cm,BC=5cm
a) Chứng tỏ tam giác ABC vuông tại A.
b) Trên tia đối của tia AC lấy điểm D sao cho CD=6cm.Tính độ dài đoạn thẳng BD.
2.Cho tam giác ABC, biết AB = 12cm,AC = 9cm,BC = 15cm.
a) Chứng tỏ tam giác ABC vuông.
b) Kẻ AH vuông góc với BC tại H, biết AH = 7,2cm.Tính độ dài đoạn thẳng BH và HC.
3.Cho tam giác nhọn ABC(AB<AC). Kẻ AH vuông góc với BC tại H. Tính chu vi tam giác ABC biết AC = 20cm, AH = 12cm, BH = 5cm.
4.Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC
a) Chứng minh tam giác AHB = tam giác AHC
b) Từ H kẻ HM vuông góc với AB tại M. Trên cạnh AC lấy điểm N sao cho BM = CN. Chứng minh HN vuông góc AC.
5.Cho tam giác ABC cân tại A, tia phân giác của góc A cắt BC tại I
a) Chứng minh tam giác AIB = tam giác AIC
b) Lấy M là trung điểm AC. Trên tia đối của tia MB lấy điểm D sao cho MB = MD. Chứng minh AD song song BC và AI vuông góc AD.
c) Vẽ AH vuông góc BD tại H, vẽ CK vuông góc BD tại K. Chứng minh BH = DK.
6.Cho tam giác ABC vuông tại A, đường phân giác BD. Kẻ AE vuông góc BD(E thuộc BD). AE cắt BC ở K.
a) Chứng minh tam giác ABE = tam giác KBE và suy ra tam giác BAK cân.
b) Chứng minh tam giác ABD = tam giác KBD và DK vuông góc BC.
c) Kẻ AH vuông góc BC(H thuộc BC). Chứng minh AK là tia phân giác của HAC.
Mọi người vẽ hình lun 6 bài giúp mình nha! Mình đang cần gấp!:(
Ai đó giúp mình với! Mình đang cần gấp!:( Các bạn vẽ hình lun giúp mình nha! Cảm ơn các bạn nhìu!:)
Do tam giác ABC có
AB = 3 , AC = 4 , BC = 5
Suy ra ta được
(3*3)+(4*4)=5*5 ( định lý pi ta go)
9 + 16 = 25
Theo định lý py ta go thì tam giác abc vuông tại A
a) Áp dụng định lý Pytago vào \(\Delta\)ABC có
AB2+AC2=BC2
thay AB=3cm, AC=4cm va BC=5cm, ta có:
32+42=52
=> 9+16=25 (luôn đúng)
=> đpcm
b) có D nằm trên tia đối của tia AC
=> D,A,C thằng hàng và A nằm giữa D và C
=> DA+AC=DC
=> DA+4=6
=>DA=2(cm)
áp dụng định lý Pytago vào tam giác ABD vuông tại A có:
AB2+AD2=BD2
=> 32+22=BD2
=> 9+4=BD2
=> \(BD=\sqrt{13}\)(cm)