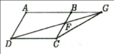
Cho Δ ABC, ∠B = ∠ C, AC - AB = 2cm, BC = 5cm. Tính AB và AC

Những câu hỏi liên quan
Trong Δ ABC có AB = 8cm và B'C'//BC. Lấy trên cạnh AB điểm B', trên cạnh AC lấy điểm C' sao cho AB' = 2cm, AC' = 3cm. Tính độ dài cạnh AC.
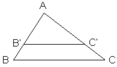
Áp dụng hệ quả trên ta có: Δ ABC, B'C'//BC; B' ∈ AB, C' ∈ AC
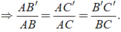
Khi đó ta có: AB'/AB = AC'/AC ⇔ 2/8 = 3/AC ⇒ AC = (3.8)/2 = 12( cm )
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB 6cm,AC 15cm. Trên AB,AC lần lượt lấy B,C sao cho AB 2cm;AC 5cm.a) Tính các tỉ số frac{{AB}}{{AB}} và frac{{AC}}{{AC}}.b) Qua B vẽ đường thẳng song song với BC cắt AC tại E. Tính AE.c) So sánh AE và AC.d) Hãy nhận xét về vị trí của E và C, vị trí của hai đường thẳng BC và BE.
Đọc tiếp
Cho tam giác \(ABC\) có \(AB = 6cm,AC = 15cm\). Trên \(AB,AC\) lần lượt lấy \(B',C'\) sao cho \(AB' = 2cm;AC' = 5cm\).
a) Tính các tỉ số \(\frac{{AB'}}{{AB}}\) và \(\frac{{AC'}}{{AC}}\).
b) Qua \(B'\) vẽ đường thẳng song song với \(BC\) cắt \(AC\) tại \(E\). Tính \(AE\).
c) So sánh \(AE\) và \(AC'\).
d) Hãy nhận xét về vị trí của \(E\) và \(C'\), vị trí của hai đường thẳng \(B'C'\) và \(B'E\).
a) Ta có:
\(\frac{{AB'}}{{AB}} = \frac{2}{6} = \frac{1}{3}\) và \(\frac{{AC'}}{{AC}} = \frac{5}{{15}} = \frac{1}{3}\).
b) Vì \(B'E//BC\) và\(B'E\) cắt \(AC\) tại \(E\) nên theo định lí Thales ta có:
\(\frac{{AB'}}{{AB}} = \frac{{AE}}{{AC}} \Rightarrow \frac{2}{6} = \frac{{AE}}{{15}} \Rightarrow AE = \frac{{2.15}}{6} = 5cm\)
c) Ta có: \(AE = AC' = 5cm\).
d) Điểm \(E \equiv C'\) và đường thẳng \(B'C' \equiv B'E\).
Đúng 1
Bình luận (0)
Trong Δ ABC có AB = 6cm, AC = 9cm. Lấy trên cạnh AB điểm B', trên cạnh AC lấy điểm C' sao cho AB' = 2cm, AC' = 3cm. Chứng minh B'C'//BC.
Trong Δ ABC, B' ∈ AB, C' ∈ AC.
Ta có
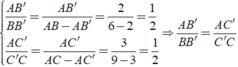
Suy ra: B'C'//BC.
Đúng 0
Bình luận (0)
Cho Δ ABC vuông tại A có góc B=300. Tia phân giác góc C cắt AB tại D. Kẻ DH vuông góc với BC (H ϵ BC).
a) C/m Δ BCD là tam giác cân và Δ ACH là tam giác đều.
b) Khi AB = 5cm. Tính BC, AC
c) Gọi I là giao điểm của HD và AC. C/m Δ IBC là tam giác đều và IC // với AH
Help mik các bạn ơi, please!
Bài 1: Cho Δ ABC vuông góc tại A có BC 5cm, AC 3cm, EF 3cm, DE DF 2,5cm. Chọn phát biểu đúng?A. Δ ABC ∼ Δ DEFB. ABCˆ EFDˆC. ACBˆ ADFˆD. ACBˆ DEFˆBài 2: Cho hai tam giác Δ RSK và Δ PQM có: RS/PQ RK/PM SK/QM thì:A. Δ RSK ∼ Δ PQMB. Δ RSK ∼ Δ MPQC. Δ RSK ∼ Δ QPMD. Δ RSK ∼ Δ QMPBài 3: Nếu Δ RSK ∼ Δ PQM có: RS/PQ RK/PM SK/QM thìA. RSKˆ PQMˆB. RSKˆ PMQˆC. RSKˆ MPQˆD. RSKˆ QPMˆBài 4: Chọn câu trả lời đúng?A. Δ ABC, Δ DEF;AB/DE AC/DF;Bˆ Eˆ ⇒ Δ ABC ∼ Δ DEFB. Δ ABC, Δ DEF;AB/DE AC/DF;Cˆ...
Đọc tiếp
Bài 1: Cho Δ ABC vuông góc tại A có BC = 5cm, AC = 3cm, EF = 3cm, DE = DF = 2,5cm. Chọn phát biểu đúng?
A. Δ ABC ∼ Δ DEF
B. ABCˆ = EFDˆ
C. ACBˆ = ADFˆ
D. ACBˆ = DEFˆ
Bài 2: Cho hai tam giác Δ RSK và Δ PQM có: RS/PQ = RK/PM = SK/QM thì:
A. Δ RSK ∼ Δ PQM
B. Δ RSK ∼ Δ MPQ
C. Δ RSK ∼ Δ QPM
D. Δ RSK ∼ Δ QMP
Bài 3: Nếu Δ RSK ∼ Δ PQM có: RS/PQ = RK/PM = SK/QM thì
A. RSKˆ = PQMˆ
B. RSKˆ = PMQˆ
C. RSKˆ = MPQˆ
D. RSKˆ = QPMˆ
Bài 4: Chọn câu trả lời đúng?
A. Δ ABC, Δ DEF;AB/DE = AC/DF;Bˆ = Eˆ ⇒ Δ ABC ∼ Δ DEF
B. Δ ABC, Δ DEF;AB/DE = AC/DF;Cˆ = Fˆ ⇒ Δ ABC ∼ Δ DEF
C. Δ ABC, Δ DEF;AB/DE = AC/DF;Aˆ = Dˆ ⇒ Δ ABC ∼ Δ DEF
D. Δ ABC, Δ DEF;AB/DE = AC/DF;Aˆ = Eˆ ⇒ Δ ABC ∼ Δ DEF
Bài 5: Cho hình bên, ABCD là hình thang ( AB//CD ) có AB = 12,5cm; CD = 28,5cm; DABˆ = DBCˆ. Tính độ dài đoạn BD gần nhất bằng bao nhiêu?
A. 17,5 B. 18
C. 18,5 D. 19
II. Bài tập tự luận
Bài 1: Tứ giác ABCD có AB = 2cm; BC = 6cm; CD = 8cm; DA = 3cm và BD = 4cm. Chứng minh rằng:
a) Δ BAD ∼ Δ DBC
b) ABCD là hình thang
Cho tam giác ABC có AC = 8cm, BC = 16cm Gọi D và E là hai điểm lần lượt trên cạnh AB và AC sao cho BD = 2cm CE = 13cm Chứng minh rằng a. AAEB đồng dạng AADC b. AED= ABC, cho DE = 5cm Tính BC? C. AE.AC=AD.AB
a) Ta có: AB-DB=AD=> AD=8-2=6cm
AC-EC=AE=16cm-13cm=AE=>AE=3cm
Xét △AEB và △ADC có góc A chung
AE:AD=3:6=1:2
AB:AC=8:16=1:2
=>AE:AD=AB:AC=1:2
=>△AEB đồng dạng với △ADC
Đúng 0
Bình luận (0)
b) Ta có: AE/AD=AB/AC(cmt)=>AE/AB=AD/AC
Xét △AED và △ABC có:
EAD=BAC
AE/AB=AD/AC
=> AED=ABC .
Đúng 0
Bình luận (0)
a: Sửa đề: AB=8cm; AC=16cm
Xét ΔAEB và ΔADC có
AE/AD=AB/AC
góc A chhung
=>ΔAEB đồg dạng với ΔADC
b: AE/AD=AB/AC
=>AE/AB=AD/AC
=>ΔAED đồng dạng vói ΔABC
=>góc AED=góc ABC
ΔAED đồng dạng vói ΔABC
=>ED/BC=AE/AB
=>5/BC=3/8
=>BC=5:3/8=5*8/3=40/3cm
c: AE/AB=AD/AC
=>AE*AC=AB*AD
Đúng 0
Bình luận (0)
cho tam giác ABC, AB= 5cm, AC=7.5cm, BC=10cm. Trên cạnh AB lấy D sao cho AD=2cm, DE//BC (E thuộc AC), trên cạnh BC lấy F sao cho BF=6cm
a) Tính AE b) Chứng minh: EF//ABa) Áp dụng định lý Thales trong tam giác ABC, ta có:
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\) . Kết hợp với giả thiết ta được \(\dfrac{2}{5}=\dfrac{AE}{7,5}\) \(\Rightarrow AE=3\)
b) Ta thấy \(\dfrac{AE}{AC}=\dfrac{3}{7,5}=\dfrac{2}{5}\) nhưng \(\dfrac{BF}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\ne\dfrac{AE}{AC}\) nên theo định lý Thales đảo, ta không thể có EF//AB.
Đúng 1
Bình luận (0)
Cho tam giác ABC có AB 5cm, BC 8cm, AC 7cm. Lấy điểm D nằm trên cạnh BC sao cho
B
D
2
c
m
. Qua D kẻ các đường thẳng song song với AB và AC, cắt AC và AB lần lượt tại F và E.a) Chứng minh
Δ
B
D
E
∽
Δ
D
C
F
.
b) Tính chu vi tứ giác AEDF
Đọc tiếp
Cho tam giác ABC có AB = 5cm, BC = 8cm, AC = 7cm. Lấy điểm D nằm trên cạnh BC sao cho B D = 2 c m . Qua D kẻ các đường thẳng song song với AB và AC, cắt AC và AB lần lượt tại F và E.
a) Chứng minh Δ B D E ∽ Δ D C F .
b) Tính chu vi tứ giác AEDF
Cho tam giác ABC Hãy tính cạnh BC biết
a, AB= 1cm , AC= 2cm , góc BAC = 120 độ
b, AB= 1dm , AC = 5cm , góc BAC = 60 độ
c, AB= 2cm ,AC= \(\sqrt{3}\)cm , góc BAC = 60 độ
Áp dụng định lí Cosin :
\(BC^2=AB^2+AC^2-2AB.AC.cosA\)
Đúng 0
Bình luận (0)
a, \(\sqrt{7}\) cm
b, căn 21 cm
c, \(\sqrt{7-2\sqrt{3}}\) cm
Đúng 0
Bình luận (0)
Áp dụng định lý Cosin:
BC2 = AB2 + AC2 - 2AB.AC.cosA
Đúng 0
Bình luận (0)