Tính
A=\(\frac{2\sin^2x+3\cos^2x+3}{\sin^2x+4\cos^2x+2}\)
Những câu hỏi liên quan
Cho
1.tan α=\(\dfrac{1}{3} \) tính A=\(\dfrac{2\sin^2x+5}{4\cos^2x-3}\)
2.cot α=\(\dfrac{2}{5}\) tính B=\(\dfrac{3\cos^2x-\sin^2x}{c\text{os}^2x+2\sin^2x}\)
\(A=\dfrac{2tan^2a+\dfrac{5}{cos^2a}}{4-\dfrac{3}{cos^2a}}=\dfrac{2tan^2a+5\left(1+tan^2a\right)}{4-3\left(1+tan^2a\right)}=...\) (bạn tự thay số bấm máy nhé)
\(B=\dfrac{3cot^2a-1}{cot^2a+2}=...\)
Đúng 2
Bình luận (0)
Giải các phương trình sau :
a) \(2\sin^2x+\sin x\cos x-3\cos^2x=0\)
b) \(3\sin^2-4\sin x\cos x+5\cos^2x=2\)
c) \(\sin^2x+\sin2x-2\cos^2+5\cos^2x=2\)
d) \(2\cos^2x-3\sqrt{3}\sin2x-4\sin^2x=-4\)
a) Dễ thấy cosx = 0 không thỏa mãn phương trình đã cho nên chiaw phương trình cho cos2x ta được phương trình tương đương 2tan2x + tanx - 3 = 0.
Đặt t = tanx thì phương trình này trở thành
2t2 + t - 3 = 0 ⇔ t ∈ {1 ; 
}.
Vậy 
b) Thay 2 = 2(sin2x + cos2x), phương trình đã cho trở thành
3sin2x - 4sinxcosx + 5cos2x = 2sin2x + 2cos2x
⇔ sin2x - 4sinxcosx + 3cos2x = 0
⇔ tan2x - 4tanx + 3 = 0
⇔ 
⇔ x = 
+ kπ ; x = arctan3 + kπ, k ∈ Z.
c) Thay sin2x = 2sinxcosx ; 
= (sin2x + cos2x) vào phương trình đã cho và rút gọn ta được phương trình tương đương
sin2x + 2sinxcosx - 
cos2x = 0 ⇔ tan2x + 4tanx - 5 = 0 ⇔ 
⇔ x = + kπ ; x = arctan(-5) + kπ, k ∈ Z.
d) 2cos2x - 3√3sin2x - 4sin2x = -4
⇔ 2cos2x - 3√3sin2x + 4 - 4sin2x = 0
⇔ 6cos2x - 6√3sinxcosx = 0 ⇔ cosx(cosx - √3sinx) = 0
⇔ 
Đúng 0
Bình luận (0)
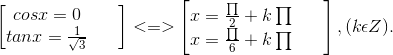
chung minh cac bieu thuc sau khong phu thuoc vao x:
a/ \(3\left(\sin^8x-\cos^8x\right)+4\left(\cos^6x-2\sin^6x\right)+6\sin^4x\)
b/\(\frac{\tan^2x-\cos^2x}{\sin^2x}+\frac{\cot^2x-\sin^2x}{\cos^2x}\)
sqrt{sin^4x+4cos^2x}+sqrt{cos^4x+4sin^2x}
sqrt{left(1-cos^2xright)^2+4cos^2x}+sqrt{left(1-sin^2xright)^2+4sin^2x}
sqrt{cos^4x-2cos^2x+1+4cos^2x}+sqrt{sin^4x-2sin^2x+1+4sin^2x}
sqrt{cos^4x+2cos^2x+1}+sqrt{sin^4x+2sin^2x+1}
sqrt{left(cos^2x+1right)^2}+sqrt{left(sin^2x+1right)^2}
cos^2x+1+sin^2x+13
Đọc tiếp
\(\sqrt{\sin^4x+4\cos^2x}+\sqrt{\cos^4x+4\sin^2x}\)
=\(\sqrt{\left(1-cos^2x\right)^2+4\cos^2x}+\sqrt{\left(1-sin^2x\right)^2+4\sin^2x}\)
=\(\sqrt{\cos^4x-2\cos^2x+1+4\cos^2x}+\sqrt{\sin^4x-2\sin^2x+1+4\sin^2x}\)
=\(\sqrt{\cos^4x+2\cos^2x+1}+\sqrt{\sin^4x+2\sin^2x+1}\)
=\(\sqrt{\left(cos^2x+1\right)^2}+\sqrt{\left(sin^2x+1\right)^2}\)
=\(cos^2x+1+sin^2x+1=3\)
giải phương trình
a, \(2\sin\frac{x}{2}\left(\sin\frac{3x}{2}+\cos\frac{3x}{2}\right)=3-4\cos x\)
b, \(\frac{2\cos^2x+\sqrt{3}\sin2x+3}{2\cos^2x.\sin\left(x+\frac{\pi}{3}\right)}=3\left(\tan^2x+1\right)\)
a/ \(cosx-cos2x+sin2x-sinx=3-4cosx\)
\(\Leftrightarrow2sinx.cosx-sinx-2cos^2x+5cosx-2=0\)
\(\Leftrightarrow sinx\left(2cosx-1\right)-\left(2cosx-1\right)\left(cosx-2\right)=0\)
\(\Leftrightarrow\left(2cosx-1\right)\left(sinx-cosx+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2cosx-1=0\\sinx-cosx=-2\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}cosx=\frac{1}{2}\\sin\left(x-\frac{\pi}{4}\right)=-\sqrt{2}< -1\left(vn\right)\end{matrix}\right.\)
\(\Rightarrow x=\pm\frac{\pi}{3}+k2\pi\)
b/ ĐKXĐ: \(\left\{{}\begin{matrix}cosx\ne0\\sin\left(x+\frac{\pi}{3}\right)\ne0\end{matrix}\right.\) \(\Rightarrow...\)
\(\frac{2cos^2x+\sqrt{3}sin2x+3}{2cos^2x.sin\left(x+\frac{\pi}{3}\right)}=\frac{3}{cos^2x}\)
\(\Leftrightarrow2cos^2x+2\sqrt{3}sinx.cosx+3=3\left(sinx+\sqrt{3}cosx\right)\)
\(\Leftrightarrow2cos^2x-3\sqrt{3}cosx+3+2\sqrt{3}sinx.cosx-3sinx=0\)
\(\Leftrightarrow\left(2cosx-\sqrt{3}\right)\left(cosx-\sqrt{3}\right)+\sqrt{3}sinx\left(2cosx-\sqrt{3}\right)=0\)
\(\Leftrightarrow\left(2cosx-\sqrt{3}\right)\left(cosx+\sqrt{3}sinx-\sqrt{3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=\frac{\sqrt{3}}{2}\\sin\left(x+\frac{\pi}{6}\right)=\frac{\sqrt{3}}{2}\end{matrix}\right.\) \(\Rightarrow...\)
Đúng 0
Bình luận (0)
Giải phương trình sau:
a) $\tan ^2x+4\cos ^2x+7=4\tan x+8\cot x$
b) $6\sin ^2x+2\cos ^2x-2\sqrt{3}\sin 2x=14\sin \left(x-\frac{\pi }{6}\right)$
Cho \(\sin x+\cos x=m\). Tính theo m các biểu thức sau:
1) \(A=\sin^2x+\cos^2x\)
2) \(B=\sin^3x+\cos^3x\)
3) \(C=\sin^4x+\cos^4x\)
4) \(D=\sin^6x+\cos^6x\)
\(sinx+cosx=m\Leftrightarrow\left(sinx+cosx\right)^2=m^2\)
\(\Leftrightarrow1+2sinx.cosx=m^2\Rightarrow sinx.cosx=\dfrac{m^2-1}{2}\)
\(A=sin^2x+cos^2x=1\)
\(B=sin^3x+cos^3x=\left(sinx+cosx\right)^3-3sinx.cosx\left(sinx+cosx\right)\)
\(=m^3-\dfrac{3m\left(m^2-1\right)}{2}=\dfrac{2m^3-3m^3+3m}{2}=\dfrac{3m-m^3}{2}\)
\(C=\left(sin^2+cos^2x\right)^2-2\left(sinx.cosx\right)^2=1-2\left(\dfrac{m^2-1}{2}\right)^2\)
\(D=\left(sin^2x\right)^3+\left(cos^2x\right)^3=\left(sin^2x+cos^2x\right)^3-3\left(sin^2x+cos^2x\right)\left(sinx.cosx\right)^2\)
\(=1-3\left(\dfrac{m^2-1}{2}\right)^2\)
Đúng 1
Bình luận (0)
Biết rằng \(A=\dfrac{4\sin^4x+\cos^4x+\sin^2x\cos^2x-3\cos^2x}{1-\cos^2x}+\dfrac{2}{\tan^2x}=a\sin^bx\) , với a, b là các số tự nhiên và \(x\ne\dfrac{k\pi}{2}\left(k\in Z\right)\) . Tính \(T=3a+4b\)
\(A=\dfrac{4sin^4x-cos^2x\left(1-cos^2x\right)+sin^2x.cos^2x-2cos^2x}{sin^2x}+\dfrac{2}{tan^2x}\)
\(=\dfrac{4sin^4x-sin^2x.cos^2x+sin^2x.cos^2x-2cos^2x}{sin^2x}+2cot^2x\)
\(=4sin^2x-2cot^2x+2cot^2x=4sin^2x\)
\(\Rightarrow\left\{{}\begin{matrix}a=4\\b=2\end{matrix}\right.\)
Đúng 3
Bình luận (0)
Giải các phương trình sau :
a) \(\cos^2x+2\sin x\cos x+5\sin^2x=2\)
b) \(3\cos^2x-2\sin2x+\sin^2x=1\)
c) \(4\cos^2x-3\sin x\cos x+3\sin^2x=1\)
