Trên đường tròn lượng giác, hãy biểu diễn các góc lượng giác có số đo có dạng:

a)     \(\frac{\pi }{4} + k\pi \,\,\left( {k \in Z} \right)\)

b)     \(k\frac{\pi }{4}\,\,\left( {k \in Z} \right)\)

Biểu diễn các góc lượng giác sau trên đường tròn lượng giác:

a)     \(\frac{{ - 17\pi }}{3}\)

b)     \(\frac{{13\pi }}{4}\)

c)     \( - 765^\circ \)

Góc lượng giác \(\frac{{31\pi }}{7}\) có cùng biểu diễn trên đường tròn lượng giác với góc lượng giác nào sau đây?

\(\frac{{3\pi }}{7};\,\,\frac{{10\pi }}{7};\,\,\frac{{ - 25\pi }}{7}\)

Cung có số đo \(\dfrac{\pi}{6}+\dfrac{k2\pi}{3}\left(k\in Z\right)\) biểu diễn được bao nhiêu điểm trên đường tròn lượng giác

Cho \(\alpha  = \frac{\pi }{3}\). Biểu diễn các góc lượng giác \( - \alpha ,\alpha  + \pi ,\pi  - \alpha ,\frac{\pi }{2} - \alpha \) trên đường tròn lượng giác và rút ra mỗi liên hệ giữ giá trị lượng giác của các góc này với giá trị lượng giác của góc \(\alpha \)

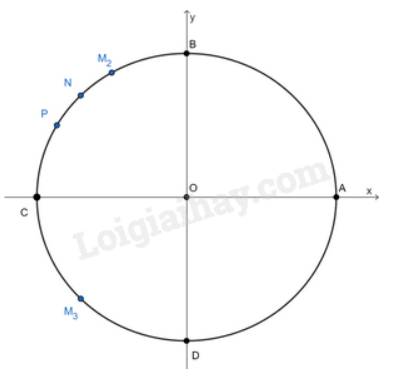
Trên đường tròn lượng giác, xác định điểm M biểu diễn các góc lượng giác có số đo sau:

a) \(\frac{{2\pi }}{3}\);          b) \( - \frac{{11\pi }}{4}\);       c) \({150^0}\);          d) \( - {225^0}\).

Tìm điểm biểu diễn trên đường tròn lượng giác của góc α = \(\dfrac{\pi}{2}+k\pi\left(k\in Z\right)\)

Sử dụng đường tròn lượng giác hãy viết ghép chung lại số đo hai cung lượng giác sau

a) \(\frac\pi3+k2\pi \) và \(\frac{4\pi}{3}+k2\pi\)

b) \(\frac{2\pi}{3}+k\pi\) và \(\frac\pi3+k\pi\)

c) \(\frac{\pi}{12}+\frac{k\pi}{2}\) và \(\frac\pi3+\frac{k\pi}{2}\)