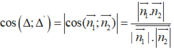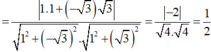2x+4y-1=0

=>VTPT là (2;4)

x-3y+1=0

=>VTPT là (1;-3)

\(cos\left(d1;d2\right)=\dfrac{\left|2\cdot1+\left(-4\right)\cdot3\right|}{\sqrt{2^2+4^2}\cdot\sqrt{1^2+\left(-3\right)^2}}=\dfrac{\sqrt{2}}{2}\)

=>\(\widehat{\left(d1;d2\right)}=45^0\)

Vectơ pháp tuyến của đường thẳng d₁ là n1=(1;2)

Vectơ pháp tuyến của đường thẳng d₂ là n2=(2;-4)

Gọi φ là góc giữa 2 đường thẳng ta có:

cos   φ   = n 1 . n 2 n 1 . n 2 = - 3 5

Chọn A.

Đáp án là C

Đáp án là C

Vecto pháp tuyến của đường thẳng \({d_1}\) là: \(\overrightarrow {{n_1}}  = \left( {2; - 1} \right)\)

Vecto pháp tuyến của đường thẳng \({d_2}\) là: \(\overrightarrow {{n_2}}  = \left( {1; - 3} \right)\)

Ta có:  \(\cos \left( {{d_1},{d_2}} \right) = \left| {\cos \left( {\overrightarrow {{n_1}} ;\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {2.1 + \left( { - 1} \right).\left( { - 3} \right)} \right|}}{{\sqrt {{{\left( 2 \right)}^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{1^2} + {{\left( { - 3} \right)}^2}} }} = \frac{{\sqrt 2 }}{2}\)

Vậy \(\left( {{d_1},{d_2}} \right) = {45^o}\)

\(d_1\) nhận \(\overrightarrow{n_1}=\left(1;3\right)\) là 1 vtpt

\(d_2\) nhận \(\overrightarrow{n_2}=\left(1;\sqrt{3}\right)\) là 1 vtpt

Gọi \(\alpha\) là góc giữa d1 và d2

\(\Rightarrow cos\alpha=\left|cos\left(\overrightarrow{n_1};\overrightarrow{n_2}\right)\right|=\dfrac{\left|1.1+3.\sqrt{3}\right|}{\sqrt{1^2+3^2}.\sqrt{1^2+3}}=\dfrac{3\sqrt{3}+1}{2\sqrt{10}}\)

\(\Rightarrow\alpha\approx11^034'\)

a) Tọa độ giao điểm của hai đường thẳng là nghiệm của hệ sau:

\(\left\{ \begin{array}{l}x - y + 2 = 0\\x + y + 4 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - 3\\y =  - 1\end{array} \right.\)

\(\cos \left( {{d_1},{d_2}} \right) = \frac{{\left| {1.1 + ( - 1).1} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{1^2} + {1^2}} }} = 0 \Rightarrow {d_1} \bot {d_2}\)

Vậy hai đường thẳng \({d_1}\) và \({d_2}\) vuông góc với nhau tại điểm có tọa độ \(( - 3; - 1)\)

b) Đường thẳng \({d_1}\) có phương trình tổng quát là: \({d_1}:2x - y + 1 = 0\)

Tọa độ giao điểm của hai đường thẳng là nghiệm của hệ sau:

\(\left\{ \begin{array}{l}2x - y + 1 = 0\\x - 3y + 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - \frac{1}{5}\\y = \frac{3}{5}\end{array} \right.\)

\(\cos \left( {{d_1},{d_2}} \right) = \frac{{\left| {2.\left( { - 1} \right) + 1.( - 3)} \right|}}{{\sqrt {{2^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{1^2} + {{\left( { - 3} \right)}^2}} }} = \frac{{\sqrt 2 }}{2} \Rightarrow \left( {{d_1},{d_2}} \right) = 45^\circ \)

Vậy hai đường thẳng \({d_1}\) và \({d_2}\) cắt nhau tại điểm có tọa độ \(\left( { - \frac{1}{5};\frac{3}{5}} \right)\) và góc giữa chúng là \(45^\circ \)

c) Đường thẳng \({d_1}\) và \({d_2}\) lần lượt có phương trình tổng quát là:

\({d_1}:3x + y - 11 = 0,{d_2}:x - 3y + 8 = 0\)

Tọa độ giao điểm của hai đường thẳng là nghiệm của hệ sau:

\(\left\{ \begin{array}{l}3x + y - 11 = 0\\x - 3y + 8 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{5}{2}\\y = \frac{7}{2}\end{array} \right.\)

\(\cos \left( {{d_1},{d_2}} \right) = \frac{{\left| {3.1 + 1.( - 3)} \right|}}{{\sqrt {{3^2} + {1^2}} .\sqrt {{1^2} + {{\left( { - 3} \right)}^2}} }} = 0 \Rightarrow \left( {{d_1},{d_2}} \right) = 90^\circ \)

Vậy hai đường thẳng \({d_1}\) và \({d_2}\) vuông góc tại điểm có tọa độ \(\left( {\frac{5}{2};\frac{7}{2}} \right)\)