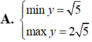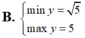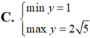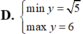tìm GTLN và GTNN của hàm số y =-2x^2 khi x tăng từ -3 đến 2

Những câu hỏi liên quan
tìm GTLN và GTNN của hàm số \(y=x^2-2x+3\)
\(y=x^2-2x+3=x^2-2x+1+2=\left(x-1\right)^2+2\ge2\)
Vậy GTNN của hàm số là 2
Đúng 0
Bình luận (0)
Tìm GTLN-GTNN của hàm số y= \(^{x^4}\)-\(2x^2\) với x thuộc [-2;1]
help me
Đạo hàm đi bạn :D Cho nhanh
\(y=f\left(x\right)=x^4-2x^2\)
\(\Rightarrow f'\left(x\right)=4x^3-4x\)
\(f'\left(x\right)=0\Leftrightarrow4x^3-4x=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\\x=0\end{matrix}\right.\)
\(f\left(1\right)=-1;f\left(-2\right)=8;f\left(-1\right)=-1;f\left(0\right)=0\)
\(\Rightarrow y_{min}=-1;"="\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
\(y_{max}=8;"="\Leftrightarrow x=-2\)
Đúng 0
Bình luận (0)
Đặt \(x^2=t\left(0\le t\le4\right)\)
\(y=f\left(t\right)=t^2-2t\)
\(minf\left(t\right)=min\left\{f\left(0\right);f\left(4\right);f\left(1\right)\right\}=f\left(1\right)=-1\)
\(maxf\left(t\right)=max\left\{f\left(0\right);f\left(4\right);f\left(1\right)\right\}=f\left(4\right)=8\)
\(min=-1\Leftrightarrow x=\pm1\)
\(max=8\Leftrightarrow x=-2\)
Đúng 1
Bình luận (0)
Tìm GTLN M và GTNN m của hàm số \(y=\sqrt{6-2x}+\sqrt{3+2x}\)
\(y\le\sqrt{2\left(6-2x+3+2x\right)}=3\sqrt{2}\)
\(y_{max}=3\sqrt{2}\) khi \(x=\dfrac{3}{4}\)
\(y\ge\sqrt{6-2x+3+2x}=3\)
\(y_{min}=3\) khi \(\left[{}\begin{matrix}x=3\\x=-\dfrac{3}{2}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Tìm GTLN và GTNN của hàm số : 1. y = sinx + 2cosx +1 / 2sinx + cosx + 3
2.y= 2sin^2sinx - 3 sinx cosx + cos^2 x
Giải phương trình : 1. 2sin^2 * 2x + sin7x -1 = sinx
2.cos 4x + 12 sin^2 x -1 = 0
Tìm gtln gtnn của hàm số y= cos^2 x - 4sin4x +3
Tìm GTLN và GTNN của hàm số: \(y=\sqrt{3-2x}+\sqrt{5-2x}\)
Lời giải:
ĐKXĐ: \(x\leq \frac{3}{2}\)
Hàm số chỉ có min chứ không có max bạn nhé.
\(y=\sqrt{3-2x}+\sqrt{5-2x}\)
\(\Rightarrow y^2=3-2x+5-2x+2\sqrt{(3-2x)(5-2x)}\)
\(=8-4x+2\sqrt{(3-2x)(5-2x)}\)
Ta thấy:
Vì \(x\leq \frac{3}{2}\Rightarrow 8-4x\geq 8-4.\frac{3}{2}=2\)
\(2\sqrt{(3-2x)(5-2x)}\geq 0\) (theo tính chất căn bậc 2)
\(\Rightarrow y^2=8-4x+2\sqrt{(3-2x)(5-2x)}\geq 2\)
\(\Rightarrow y\geq \sqrt{2}\) (do $y$ không âm)
Vậy $y_{\min}=\sqrt{2}$ khi $x=\frac{3}{2}$
Đúng 0
Bình luận (0)
Em mới học dạng này sơ sơ thôi nên không rành lắm, mọi người check giúp ạ.
ĐK x =< 3/2
Xét \(x_1< x_2\le\frac{3}{2}\)
\(y=f\left(x\right)=\sqrt{3-2x}+\sqrt{5-2x}\)
Ta có: \(f\left(x_1\right)-f\left(x_2\right)=\left(\sqrt{3-2x_1}-\sqrt{3-2x_2}\right)+\left(\sqrt{5-2x_1}-\sqrt{5-2x_2}\right)>0\)(do dễ thấy(em lười viết ra quá) rằng mỗi cái ngoặc đều lớn hơn 0)
Do đó f(x1) > f(x2). Do vậy x càng tăng thì giá trị f(x) càng nhỏ hay y đạt cực tiểu tại x = 3/2. Vậy \(y_{min}=\sqrt{3-2.\frac{3}{2}}+\sqrt{5-2.\frac{3}{2}}=\sqrt{2}\)
Đẳng thức xảy ra khi x = 3/2
Vậy...
Đúng 0
Bình luận (0)
Tìm GTLN (max), GTNN (min) của hàm số
y
x
+
2
x
với
x
∈
1
;
3
Đọc tiếp
Tìm GTLN (max), GTNN (min) của hàm số y = x + 2 x với x ∈ 1 ; 3
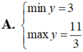
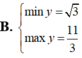
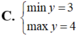
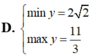
Tìm GTLN; GTNN của các hàm số
\(a,y=3-4sin^2xcos^2x\)
\(b,y=\dfrac{-2}{3sinx-5}\) trên đoạn \(\left[0;\dfrac{\pi}{2}\right]\)
a, \(y=3-4sin^2x.cos^2x=3-sin^22x\)
Đặt \(sin2x=t\left(t\in\left[-1;1\right]\right)\).
\(\Rightarrow y=f\left(t\right)=3-t^2\)
\(\Rightarrow y_{min}=minf\left(t\right)=2\)
\(y_{max}=maxf\left(t\right)=3\)
Đúng 1
Bình luận (0)
b, \(y=f\left(t\right)=\dfrac{-2}{3t-5}\left(t\in\left[0;1\right]\right)\)
\(\Rightarrow y_{min}=minf\left(t\right)=\dfrac{2}{5}\)
\(y_{max}=maxf\left(t\right)=1\)
Đúng 1
Bình luận (0)
Tìm GTLN (max); GTNN (min) của hàm số
y
2
x
+
1
+
4
-
x
.
Đọc tiếp
Tìm GTLN (max); GTNN (min) của hàm số y = 2 x + 1 + 4 - x .