Cos^2x-sin^2x=0

Những câu hỏi liên quan
Giải pt
a) \(-3\sin x\cos x+\sin^2x=2\)
b) \(2\sin^2x+\sin x\cos x-3\cos^2x=0\)
a.
Với \(cosx=0\) ko phải nghiệm
Với \(cosx\ne0\) chia 2 vế cho \(cos^2x\)
\(\Rightarrow-3tanx+tan^2x=2+2tan^2x\)
\(\Leftrightarrow tan^2x+3tanx+2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=-1\\tanx=-2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=arctan\left(-2\right)+k\pi\end{matrix}\right.\)
Đúng 2
Bình luận (0)
b.
Với \(cosx=0\) không phải nghiệm
Với \(cosx\ne0\) chia 2 vế cho \(cos^2x\)
\(\Rightarrow2tan^2x+tanx-3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=1\\tanx=-\dfrac{3}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=arctan\left(-\dfrac{3}{2}\right)+k\pi\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Chứng minh: 1.dfrac{cot^2x-sin^2x}{cot^2x-tan^2x}sin^2xcdotcos^2x 2.dfrac{1-sin x}{cos x}-dfrac{cos x}{1+sin x}0 3.dfrac{tan x}{sin x}-dfrac{sin x}{cot x}cos x 4.dfrac{tan x}{1-tan^2x}cdotdfrac{cot^2x-1}{cot x}1 5.dfrac{1+sin^2x}{1-sin^2x}1+2tan^2x
Đọc tiếp
Chứng minh:
1.\(\dfrac{\cot^2x-\sin^2x}{\cot^2x-\tan^2x}=\sin^2x\cdot\cos^2x\)
2.\(\dfrac{1-\sin x}{\cos x}-\dfrac{\cos x}{1+\sin x}=0\)
3.\(\dfrac{\tan x}{\sin x}-\dfrac{\sin x}{\cot x}=\cos x\)
4.\(\dfrac{\tan x}{1-\tan^2x}\cdot\dfrac{\cot^2x-1}{\cot x}=1\)
5.\(\dfrac{1+\sin^2x}{1-\sin^2x}=1+2\tan^2x\)
Câu 1 đề sai, chắc chắn 1 trong 2 cái \(cot^2x\) phải có 1 cái là \(cos^2x\)
2.
\(\dfrac{1-sinx}{cosx}-\dfrac{cosx}{1+sinx}=\dfrac{\left(1-sinx\right)\left(1+sinx\right)-cos^2x}{cosx\left(1+sinx\right)}=\dfrac{1-sin^2x-cos^2x}{cosx\left(1+sinx\right)}\)
\(=\dfrac{1-\left(sin^2x+cos^2x\right)}{cosx\left(1+sinx\right)}=\dfrac{1-1}{cosx\left(1+sinx\right)}=0\)
3.
\(\dfrac{tanx}{sinx}-\dfrac{sinx}{cotx}=\dfrac{tanx.cotx-sin^2x}{sinx.cotx}=\dfrac{1-sin^2x}{sinx.\dfrac{cosx}{sinx}}=\dfrac{cos^2x}{cosx}=cosx\)
4.
\(\dfrac{tanx}{1-tan^2x}.\dfrac{cot^2x-1}{cotx}=\dfrac{tanx}{1-tan^2x}.\dfrac{\dfrac{1}{tan^2x}-1}{\dfrac{1}{tanx}}=\dfrac{tanx}{1-tan^2x}.\dfrac{1-tan^2x}{tanx}=1\)
5.
\(\dfrac{1+sin^2x}{1-sin^2x}=\dfrac{1+sin^2x}{cos^2x}=\dfrac{1}{cos^2x}+tan^2x=\dfrac{sin^2x+cos^2x}{cos^2x}+tan^2x\)
\(=tan^2x+1+tan^2x=1+2tan^2x\)
Đúng 3
Bình luận (0)
Sin 2x - cos 2x +3 sin x - cos x - 1 = 0
<=> 2.sinx.cosx - 1 + 2.sin2x + 3.sinx - cosx - 1 = 0
<=> cosx.( 2.sinx - 1 ) + ( 2.sinx - 1 ).( sinx + 2) = 0
<=> (2.sinx - 1 ).( cosx + sinx + 2 ) = 0
<=> \(\left[{}\begin{matrix}2.sinx-1=0\\cosx+sinx=2\left(VN\right)\end{matrix}\right.\)
<=> sinx = \(\dfrac{1}{2}\)
<=> \(\left[{}\begin{matrix}x=\dfrac{\pi}{6}+2k\pi\\x=\dfrac{5\pi}{6}+2k\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
1. Tìm m để PT có nghiệm:
a) \(\sqrt{3}\cos^2x+\dfrac{1}{2}\sin2x=m\)
b) \(3\sin^2x-2\sin x\cos x+m=0\)
c) \(\sin^2x+2\left(m-1\right)\sin x\cos x-\left(m+1\right)\cos^2x=m\)
b.
\(\Leftrightarrow\dfrac{3}{2}\left(1-cos2x\right)-sin2x+m=0\)
\(\Leftrightarrow sin2x+\dfrac{3}{2}cos2x-\dfrac{3}{2}=m\)
\(\Leftrightarrow\dfrac{\sqrt{13}}{2}\left(\dfrac{2}{\sqrt{13}}sin2x+\dfrac{3}{\sqrt{13}}cos2x\right)-\dfrac{3}{2}=m\)
Đặt \(\dfrac{2}{\sqrt{13}}=cosa\) với \(a\in\left(0;\dfrac{\pi}{2}\right)\)
\(\Rightarrow\dfrac{\sqrt{13}}{2}sin\left(2x+a\right)-\dfrac{3}{2}=m\)
Phương trình có nghiệm khi và chỉ khi:
\(\dfrac{-\sqrt{13}-3}{2}\le m\le\dfrac{\sqrt{13}-3}{2}\)
Đúng 2
Bình luận (0)
Lý thuyết đồ thị:
Phương trình \(f\left(x\right)=m\) có nghiệm khi và chỉ khi \(f\left(x\right)_{min}\le m\le f\left(x\right)_{max}\)
Hoặc sử dụng điều kiện có nghiệm của pt lương giác bậc nhất (tùy bạn)
a.
\(\dfrac{\sqrt{3}}{2}\left(1-cos2x\right)+\dfrac{1}{2}sin2x=m\)
\(\Leftrightarrow\dfrac{1}{2}sin2x-\dfrac{\sqrt{3}}{2}cos2x+\dfrac{\sqrt{3}}{2}=m\)
\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{3}\right)+\dfrac{\sqrt{3}}{2}=m\)
\(\Rightarrow\) Pt có nghiệm khi và chỉ khi:
\(-1+\dfrac{\sqrt{3}}{2}\le m\le1+\dfrac{\sqrt{3}}{2}\)
Đúng 3
Bình luận (0)
c.
\(\Leftrightarrow\dfrac{1}{2}-\dfrac{1}{2}cos2x+\left(m-1\right)sin2x-\left(m+1\right)\left(\dfrac{1}{2}+\dfrac{1}{2}cos2x\right)=m\)
\(\Leftrightarrow\left(2m-2\right)sin2x-\left(m+2\right)cos2x=3m\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất, pt có nghiệm khi:
\(\left(2m-2\right)^2+\left(m+2\right)^2\ge9m^2\)
\(\Leftrightarrow m^2+m-2\le0\)
\(\Leftrightarrow-2\le m\le\)
Đúng 2
Bình luận (0)
1. Tìm m để PT có nghiệm:
a) \(\sqrt{3}\cos^2x+\dfrac{1}{2}\sin2x=m\)
b) \(3\sin^2x-2\sin x\cos x+m=0\)
c) \(^{ }\sin^2x+2\left(m-1\right)\sin x\cos x-\left(m+1\right)\cos^2x=m\)
a) \(\sqrt{3}\left(\dfrac{1+cos2x}{2}\right)+\dfrac{1}{2}sin2x=m\) ↔ \(\dfrac{\sqrt{3}}{2}cos2x+\dfrac{1}{2}sin2x=m-\dfrac{\sqrt{3}}{2}\)
→\(\sqrt{3}cos2x+sin2x=2m-\sqrt{3}\) ↔ \(2cos\left(\dfrac{\pi}{6}-2x\right)=2m-\sqrt{3}\)
→\(cos\left(\dfrac{\pi}{6}-2x\right)=m-\dfrac{\sqrt{3}}{2}\)
Pt có nghiệm khi và chỉ khi \(-1\le m-\dfrac{\sqrt{3}}{2}\le1\)
b) \(\left(3+m\right)sin^2x-2sinx.cosx+mcos^2x=0\)
cosx=0→ sinx=0=> vô lý
→ sinx#0 chia cả 2 vế của pt cho cos2x ta đc:
\(\left(3+m\right)tan^2x-2tanx+m=0\)
pt có nghiệm ⇔ △' ≥0
Tự giải phần sau
c) \(\left(1-m\right)sin^2x+2\left(m-1\right)sinx.cosx-\left(2m+1\right)cos^2x=0\)
⇔cosx=0→sinx=0→ vô lý
⇒ cosx#0 chia cả 2 vế pt cho cos2x
\(\left(1-m\right)tan^2x+2\left(m-1\right)tanx-\left(2m+1\right)=0\)
pt có nghiệm khi và chỉ khi △' ≥ 0
Tự giải
Đúng 1
Bình luận (0)
Giải các phương trình sau :
a) \(2\sin^2x+\sin x\cos x-3\cos^2x=0\)
b) \(3\sin^2-4\sin x\cos x+5\cos^2x=2\)
c) \(\sin^2x+\sin2x-2\cos^2+5\cos^2x=2\)
d) \(2\cos^2x-3\sqrt{3}\sin2x-4\sin^2x=-4\)
a) Dễ thấy cosx = 0 không thỏa mãn phương trình đã cho nên chiaw phương trình cho cos2x ta được phương trình tương đương 2tan2x + tanx - 3 = 0.
Đặt t = tanx thì phương trình này trở thành
2t2 + t - 3 = 0 ⇔ t ∈ {1 ; ![]() }.
}.
Vậy ![]()
b) Thay 2 = 2(sin2x + cos2x), phương trình đã cho trở thành
3sin2x - 4sinxcosx + 5cos2x = 2sin2x + 2cos2x
⇔ sin2x - 4sinxcosx + 3cos2x = 0
⇔ tan2x - 4tanx + 3 = 0
⇔ ![]()
⇔ x = ![]() + kπ ; x = arctan3 + kπ, k ∈ Z.
+ kπ ; x = arctan3 + kπ, k ∈ Z.
c) Thay sin2x = 2sinxcosx ; ![]() =
= ![]() (sin2x + cos2x) vào phương trình đã cho và rút gọn ta được phương trình tương đương
(sin2x + cos2x) vào phương trình đã cho và rút gọn ta được phương trình tương đương
![]() sin2x + 2sinxcosx -
sin2x + 2sinxcosx - ![]() cos2x = 0 ⇔ tan2x + 4tanx - 5 = 0 ⇔
cos2x = 0 ⇔ tan2x + 4tanx - 5 = 0 ⇔ ![]()
⇔ x = ![]() + kπ ; x = arctan(-5) + kπ, k ∈ Z.
+ kπ ; x = arctan(-5) + kπ, k ∈ Z.
d) 2cos2x - 3√3sin2x - 4sin2x = -4
⇔ 2cos2x - 3√3sin2x + 4 - 4sin2x = 0
⇔ 6cos2x - 6√3sinxcosx = 0 ⇔ cosx(cosx - √3sinx) = 0
⇔ 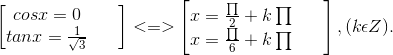
Đúng 0
Bình luận (0)
Chứng minh rằng với \(0^0\le x\le180^0\) ta có :
a) \(\left(\sin x+\cos x\right)^2=1+2\sin x\cos x\)
b) \(\left(\sin x-\cos x\right)^2=1-2\sin x\cos x\)
c) \(\sin^4x+\cos^4x=1-2\sin^2x\cos^2x\)
a) \(\left(sinx+cosx\right)^2=sin^2x+2sinxcosx+cos^2x\)\(=1+2sinxcosx\).
b) \(\left(sinx-cosx\right)^2=sin^2x-2sinxcosx+cos^2x\)\(=1-2sinxcosx\).
c) \(sin^4x+cos^4x=\left(sin^2x+cos^2x\right)^2-2sin^2xcos^2x\)
\(=1-2sin^2xcos^2x\).
Đúng 0
Bình luận (0)
Giải phương trình lượng giác sau
1) 2 cos 2x -sqrt{3} 0
2)sqrt{3} tan x + 1 0
3) 2 cos2x 1
4) 6 sin2 x- 13 sin x + 5 0
5) 5 cos 2x + 6 cos x + 1 0
6 ) 2 cos 2 2x - 3 cos 2x + 1 0
7) tan 2 x + ( 1 - sqrt{3}) tan x - sqrt{3} 0
8) cos 6x + 2 sin 3x + 3 0
9) cos 2x - 4 cos x - 5 0
10 ) 3 cos 2 x 2 sin 2 x + 4 sin x
11) cos 2x + sin2x + 2 cos x + 1 0
12) cos 4x + sin 4x + sin 2x dfrac{5}{2}
Đọc tiếp
Giải phương trình lượng giác sau
1) 2 cos 2x -\(\sqrt{3}\) = 0
2)\(\sqrt{3}\) tan x + 1 = 0
3) 2 cos2x = 1
4) 6 sin2 x- 13 sin x + 5 = 0
5) 5 cos 2x + 6 cos x + 1 = 0
6 ) 2 cos 2 2x - 3 cos 2x + 1 = 0
7) tan 2 x + ( 1 - \(\sqrt{3}\)) tan x - \(\sqrt{3}\) = 0
8) cos 6x + 2 sin 3x + 3 = 0
9) cos 2x - 4 cos x - 5 = 0
10 ) 3 cos 2 x = 2 sin 2 x + 4 sin x
11) cos 2x + sin2x + 2 cos x + 1 = 0
12) cos 4x + sin 4x + sin 2x = \(\dfrac{5}{2}\)
\(3\cos^4x-4\cos^2x\sin^2x+\sin^4x=0\)
rút gọn biểu thức sau:
B=\(\dfrac{1-4\sin^2x.\cos^2x}{\left(\sin x+\cos x\right)^2}+2\sin x.\cos x\) , với 0 độ<x<90 độ
\(B=\dfrac{1-4\sin^2x\cdot\cos^2x}{\sin^2x+2\sin x\cdot\cos x+\cos^2}+2\sin x\cdot\cos x\\ B=\dfrac{1-4\sin^2x\cdot\cos^2x}{2\sin x\cdot\cos x}+2\sin x\cdot\cos x\\ B=\dfrac{1-4\sin^2x\cdot\cos^2x+4\sin^2x\cdot\cos^2x}{2\sin x\cdot\cos x}=\dfrac{1}{2\sin x\cdot\cos x}\)
Đúng 1
Bình luận (0)















 ũ 4
ũ 4

