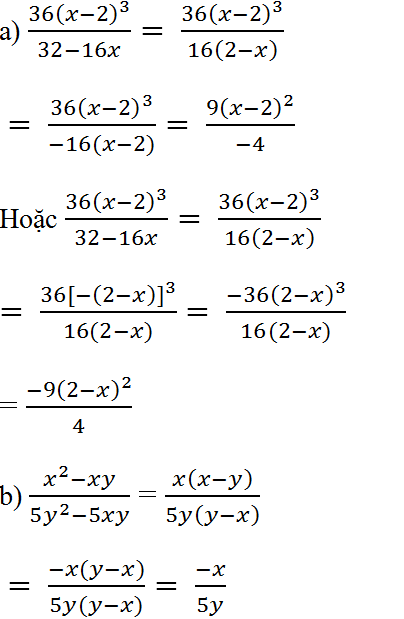a) \(\dfrac{6x^2y^2}{8xy^5}=\dfrac{3x}{4y^3}\)

b) \(=\dfrac{2y}{3\left(x+y\right)^2}=\dfrac{2y}{3x^2+6xy+3y^2}\)

c) \(=\dfrac{2x\left(x+1\right)}{x+1}=2x\)

d) \(=\dfrac{x\left(x-y\right)-\left(x-y\right)}{x\left(x+y\right)-\left(x+y\right)}=\dfrac{\left(x-y\right)\left(x-1\right)}{\left(x+y\right)\left(x-1\right)}=\dfrac{x-y}{x+y}\)

e) \(=\dfrac{36\left(x-2\right)^3}{-16\left(x-2\right)}=-9\left(x-2\right)^2=-9x^2+36x-36\)

a) \(\dfrac{36\left(x-2\right)^3}{32-16x}=\dfrac{36\left(x-2\right)^3}{16\left(2-x\right)}=\dfrac{36\left(x-2\right)^3}{-16\left(x-2\right)}\)\(=\dfrac{36\left(x-2\right)^3:4\left(x-2\right)}{-16\left(x-2\right):4\left(x-2\right)}\)\(=\dfrac{9\left(x-2\right)^2}{-4}\)

b) \(\dfrac{x^2-xy}{5y^2-5xy}=\dfrac{x\left(x-y\right)}{5y\left(y-x\right)}=\dfrac{x\left(x-y\right)}{-5y\left(x-y\right)}\)\(=\dfrac{x}{-5y}\)

a)

\(\dfrac{36\left(x-2\right)^3}{32-16x}=\dfrac{9\left(x-2\right)^3}{8-4x}=\dfrac{9\left(x-2\right)^3}{4\left(2-x\right)}=\dfrac{9\left(x-2\right)^3}{-4\left(x-2\right)}=\dfrac{9\left(x-2\right)^2}{-4}\)

b)

\(\dfrac{x^2+2x+1}{x+1}=\dfrac{\left(x+1\right)^2}{x+1}=x+1\)

c)

\(\dfrac{x^2-2x+1}{x^2-1}=\dfrac{\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}=\dfrac{x-1}{x+1}\)

Lời giải:

a) \(\frac{45x(3-x)}{15(x-3)^3}=\frac{-45x(x-3)}{15(x-3)^3}=\frac{-3x}{(x-3)^2}\)

b) \(\frac{36(x-2)^3}{32-16x}=\frac{36(x-2)^3}{-16(x-2)}=\frac{-9}{4}(x-2)^2\)

c) \(\frac{x^2-xy}{5y^2-5xy}=\frac{x(x-y)}{-5y(x-y)}=\frac{x}{-5y}\)

d) \(\frac{y^2-x^2}{x^3-3x^2y+3xy^2-y^3}=\frac{-(x^2-y^2)}{(x-y)^3}=\frac{-(x-y)(x+y)}{(x-y)^3}=\frac{-(x+y)}{(x-y)^2}\)

a, =x-z

b,=-9(2-x)^2/4

c,=x+1

d,=(x-1)/(x+1)

hok tốt

a) =\(\frac{x-z}{2}\)

bài 2 tìm x

a,106- ( x+ 7) =9

x+7 = 106 - 9

x+7 = 107

x= 107 - 7

x=100

b, 2 x ( x+ 4) + 5 =65

2 x (x+4) = 65 - 5

2 x (x+4) = 60

x+4 = 60:2

x+4= 30

x= 30 - 4

x=26

c, (16x x -32) x 45=0

16 x X - 32 = 0: 45

16 x X - 32 =0

16 x X = 0 + 32

16 x X = 32

X= 32:16

X=2

d, x+4 x x = 100 : 5

X + 4 x X = 20

(1+4) x X = 20

5 x X  = 20

X= 20:5

X=4

Bài 1:

a, 24 x 66 - 24 + 36 x 24

= 24 x (66-1+36)

= 24 x 101

= 24 x 100 + 24

= 2400+24

=2424

b, 29 x 173 - 29 x 72 - 29

= 29 x (173 - 72 -1)

= 29 x 100

= 2900

c, 1+5+10+15+...+55+60

= (5+60) x 6 + 1 (có 6 cặp)

= 65 x 6 + 1

= 390 +1 =391

d, D= 1 x 2 + 2 x 3 + 3 x 4 +...+18 x 19 + 19 x 20

3D= 1 x 2 x 3+ 2 x 3 x (4-1) + 3 x 4 x (5-2) +...+ 18 x 19 x (20 - 17) + 19 x 20 x (21-18)

3D= 1 x 2 x 3 - 1 x 2 x 3 + 2 x 3 x 4 - 2 x 3 x 4 +.... + 19 x 20 x 21 - 18 x 19 x 20

3D= 19 x 20 x 21 =7980

=> D= 7980:3=2660

a) \(\sqrt{1-8x+16x^2}=\dfrac{1}{3}\)

\(\Leftrightarrow\sqrt{1^2-2\cdot4x\cdot1+\left(4x\right)^2}=\dfrac{1}{3}\)

\(\Leftrightarrow\sqrt{\left(4x-1\right)^2}=\dfrac{1}{3}\)

\(\Leftrightarrow\left|4x-1\right|=\dfrac{1}{3}\)

\(\Leftrightarrow\left[{}\begin{matrix}4x-1=\dfrac{1}{3}\left(ĐK:x\ge\dfrac{1}{4}\right)\\4x-1=\dfrac{1}{3}\left(ĐK:x< \dfrac{1}{4}\right)\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}4x=\dfrac{4}{3}\\4x=\dfrac{2}{3}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\left(tm\right)\\x=\dfrac{1}{6}\left(tm\right)\end{matrix}\right.\)

b) \(\sqrt{16x-32}+\sqrt{25x-50}=18+\sqrt{9x-18}\) (ĐK: \(x\ge2\)) 

\(\Leftrightarrow\sqrt{16\left(x-2\right)}+\sqrt{25\left(x-2\right)}=18+\sqrt{9\left(x-2\right)}\)

\(\Leftrightarrow4\sqrt{x-2}+5\sqrt{x-2}=18+3\sqrt{x-2}\)

\(\Leftrightarrow6\sqrt{x-2}=18\)

\(\Leftrightarrow\sqrt{x-2}=3\)

\(\Leftrightarrow x-2=9\)

\(\Leftrightarrow x=9+2\)

\(\Leftrightarrow x=11\left(tm\right)\)