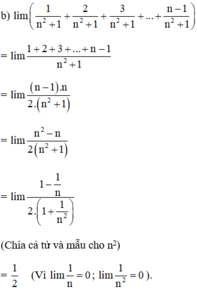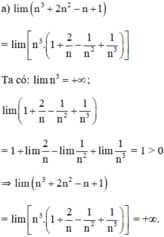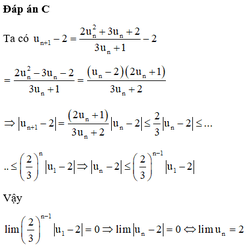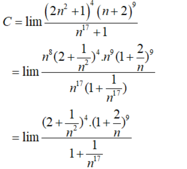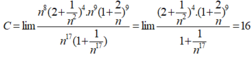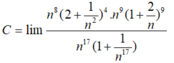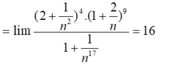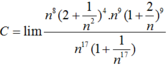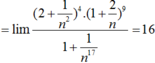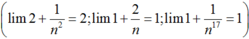Biết lim(1-n+2n2 )/ n+1 -an-b=0. Tính 2a+3b\(\)

Những câu hỏi liên quan
Cho 0<trị tuyệt đối a<1 và 0<trị tuyệt đối b<1,(a,b∈Q) thỏa mãn
\(lim\dfrac{1+a+a^2+...+a^n}{1+b+b^2+...+b^n}=\dfrac{2}{3}\).Tính T =2a-3b
\(\lim\dfrac{1+a+...+a^n}{1+b+...+b^n}=\lim\dfrac{\dfrac{1-a^n}{1-a}}{\dfrac{1-b^n}{1-b}}=\lim\dfrac{\left(1-a^n\right)\left(1-b\right)}{\left(1-b^n\right)\left(1-a\right)}=\dfrac{1-b}{1-a}\)
\(\Rightarrow\dfrac{1-b}{1-a}=\dfrac{2}{3}\Leftrightarrow3-3b=2-2a\)
\(\Leftrightarrow2a-3b=-1\)
Đúng 1
Bình luận (0)
Tính các giới hạn:
l
i
m
1
n
2
+
1
+
2
n
2
...
Đọc tiếp
Tính các giới hạn: l i m 1 n 2 + 1 + 2 n 2 + 1 + . . . + n - 1 n 2 + 1
Tính các giới hạn sau: l i m n 3 + 2 n 2 - n + 1
Cho dãy số có
u
1
1
và
u
n
+
1
2
n
2
+
3
u
n
+
2
3
u
n...
Đọc tiếp
Cho dãy số có u 1 = 1 và u n + 1 = 2 n 2 + 3 u n + 2 3 u n + 2 , n ∈ ℕ * . Tính l i m u n
A. 0
B. 1
C. 2
D. 3
cho a, b là các số thực thỏa mãn lim \(\dfrac{an^3+bn^2+2n+4}{n^2+1}=1\). tính tổng 2a+b?
Nếu \(a\ne0\Rightarrow\lim\dfrac{an^3+bn^2+2n+4}{n^2+1}=\lim\dfrac{an+b+\dfrac{2}{n}+\dfrac{4}{n^2}}{1+\dfrac{1}{n}}=\infty\) ko thỏa mãn
\(\Rightarrow a=0\)
Khi đó: \(\lim\dfrac{bn^2+2n+4}{n^2+1}=\lim\dfrac{b+\dfrac{2}{n}+\dfrac{4}{n^2}}{1+\dfrac{1}{n^2}}=b\Rightarrow b=1\)
\(\Rightarrow2a+b=1\)
Đúng 2
Bình luận (0)
Giá trị của
C
l
i
m
(
2
n
2
+
1
)
4
(
n
+
2
)
9
n
17
+
1
bằng: A.
+
∞
C. ...
Đọc tiếp
Giá trị của C = l i m ( 2 n 2 + 1 ) 4 ( n + 2 ) 9 n 17 + 1 bằng:
A. + ∞
C. - ∞
C. 16
D. 1
Giá trị của
C
l
i
m
(
2
n
2
+
1
)
4
(
n
+
2
)
9
n
17
+
1
bằng A.
+
∞
B. ...
Đọc tiếp
Giá trị của C = l i m ( 2 n 2 + 1 ) 4 ( n + 2 ) 9 n 17 + 1 bằng
A. + ∞
B. - ∞
C. 16
D. 1
Giá trị của
C
l
i
m
(
2
n
2
+
1
)
4
(
n
+
2
)
9
n
17
+
1
bằng A.
+
∞
B. ...
Đọc tiếp
Giá trị của C = l i m ( 2 n 2 + 1 ) 4 ( n + 2 ) 9 n 17 + 1 bằng
A. + ∞
B. - ∞
C. 16
D. 1
Giá trị của
C
l
i
m
2
n
2
+
1
4
(
n
+
2
)
9...
Đọc tiếp
Giá trị của C = l i m 2 n 2 + 1 4 ( n + 2 ) 9 n 17 + 1 bằng:
A. +∞
B. -∞
C. 16
D. 1