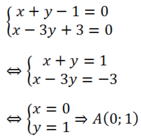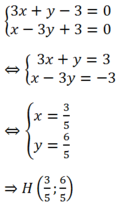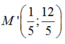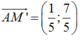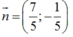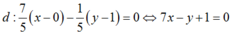1,Lập phương trình đường thẳng \(\Delta\) đi qua điểm d1: x + 3y - 1 = 0 ; d2: x - 3y - 5 = 0 và vuông góc đường thẳng d3:2x - y + 7 =0
2,Đường thẳng \(\Delta\) đi qua giao điểm của 2 đường thẳng d1: 2x + y - 3 = 0 và d2: x - 2y + 1 = 0 đồng thời tạo với đường thẳng d3: y - 1 = 0 một góc 45* của phương trình