viết phương trình đường thẳng Δ đi qua A(-1;2) và cách B(3;5) một khoảng bằng 3.

Những câu hỏi liên quan
Trong mặt phẳng toạ độ Oxy, cho hai điểm A(3;1),B(4;-2) và đường thẳng d: -x+2y+1=0. a) Viết phương trình tham số của Δ đi qua A song song với đường thẳng d b) Viết phương trình tổng quát của Δ đi qua B và vuông góc với đường thẳng d c) Viết phương trình đường tròn có bán kính AB
a: (Δ)//d nên Δ: -x+2y+c=0
=>VTPT là (-1;2)
=>VTCP là (2;1)
PTTS là:
x=3+2t và y=1+t
b: (d): -x+2y+1=0
=>Δ: 2x+y+c=0
Thay x=4 và y=-2 vào Δ, ta được:
c+8-2=0
=>c=-6
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy,cho hai điểm A(2;5); B(5;1) và đường thẳng (Δ):3x+4y-1=0
a)Viết phương trình đường thẳng đi qua hai điểm A,B
b)Viết phương trình đường thẳng (D) vuông góc với đường thẳng (Δ) và (D) cách điểm B một khoảng băng \(\dfrac{1}{5}\)
a.
\(\overrightarrow{AB}=\left(3;-4\right)\Rightarrow\) đường thẳng AB nhận (4;3) là 1 vtpt
Phương trình AB:
\(4\left(x-2\right)+3\left(y-5\right)=0\Leftrightarrow4x+3y-23=0\)b.
Do d vuông góc delta nên d nhận (4;-3) là 1 vtpt
Phương trình d có dạng: \(4x-3y+c=0\)
\(d\left(B;d\right)=\dfrac{\left|4.5-3.1+c\right|}{\sqrt{4^2+\left(-3\right)^2}}=\dfrac{1}{5}\)
\(\Rightarrow\left|c+17\right|=1\Rightarrow\left[{}\begin{matrix}c=-16\\c=-18\end{matrix}\right.\)
Có 2 đường thẳng d thỏa mãn: \(\left[{}\begin{matrix}4x-3y-16=0\\4x-3y-18=0\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Viết phương trình đường thẳng (d) đi qua điểm A\(\left(3;-1\right)\) và song song với đường thẳng (Δ): 2x + 3y - 1 = 0
\(\Delta:2x+3y-1=0.\)
\(\Rightarrow\) VTPT của \(\Delta\) là \(\overrightarrow{n_{\left(\Delta\right)}}=\left(2;3\right).\)
Phương trình đường thẳng \(\left(d\right)\) song song với đường thẳng \(\Delta:2x+3y-1=0.\)
\(\Rightarrow\) VTPT của đường thẳng \(\Delta\) cũng là VTPT của đường thẳng \(\left(d\right).\)
\(\Rightarrow\) VTPT của \(\left(d\right)\) là \(\overrightarrow{n_{\left(d\right)}}=\left(2;3\right).\)
Ta có đường thẳng \(\left(d\right)\) nhận \(\overrightarrow{n_{\left(d\right)}}=\left(2;3\right)\) làm VTPT; đi qua điểm \(A\left(3;-1\right).\)
\(\Rightarrow\) Phương trình đường thẳng \(\left(d\right)\) là:
\(2\left(x-3\right)+3\left(y+1\right)=0.\\ \Leftrightarrow2x-6+3y+3=0.\\ \Leftrightarrow2x+3y-3=0.\)
Đúng 1
Bình luận (0)
Cho điểm A(-1; 2; -3), vectơ
a
→
(6; -2; -3) và đường thẳng d có phương trình:
x
1
+
3
t
y
-
1
+
2...
Đọc tiếp
Cho điểm A(-1; 2; -3), vectơ a → = (6; -2; -3) và đường thẳng d có phương trình: x = 1 + 3 t y = - 1 + 2 t z = 3 - 5 t Viết phương trình đường thẳng Δ đi qua điểm A, vuông góc với a → và cắt đường thẳng d.
(α) ⊥ a →
Δ ⊥ a →
⇒ Δ song song hoặc nằm trong (α).
Mà Δ và (α) cùng đi qua A
⇒ Δ ⊂ (α)
Δ cắt d ⇒ Δ cắt d tại M
⇒ Δ chính là đường thẳng AM.
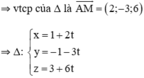
Đúng 0
Bình luận (0)
Cho A(1;-1) và B(3;0) . Viết phương trình đường thẳng d đi qua A và B biết Δ=x-2y-4=0
Phương trình đường thẳng AB có dạng \(y=ax+b\)
Từ giả thiết suy ra \(\left\{{}\begin{matrix}a+b=-1\\3a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=-\dfrac{3}{2}\end{matrix}\right.\)
\(\Rightarrow y=\dfrac{1}{2}x-\dfrac{3}{2}\)
Đúng 1
Bình luận (0)
Đường thẳng Δ có phương trình tham số: \(\left\{{}\begin{matrix}x=1+2t\\y=-3-t\end{matrix}\right.\) và 2 điểm M(2;3), N(4;2)
Viết phương trình đường thẳng d' đi qua O biết (Δ,d')=450
Lời giải:Điểm M,N có vẻ không có vai trò gì trong bài toán.
Ta có: $\overrightarrow{u_{\Delta}}=(2,-1)$
$\overrightarrow{u_{d'}}=(a,b)$
\(\cos (\Delta, d')=\frac{\overrightarrow{u_{\Delta}}.\overrightarrow{u_d'}}{|\overrightarrow{u_{\Delta}}||\overrightarrow{u_d'}|}=\frac{2a-b}{\sqrt{a^2+b^2}.\sqrt{5}}=\cos 45^0=\frac{\sqrt{2}}{2}\)
$\Rightarrow a=3b$ hoặc $a=-\frac{b}{3}$
PTĐT $d'$ là:
$-x+3y=0$ hoặc $3x+y=0$
Đúng 0
Bình luận (1)
Lập phương trình thanh số, phương trình tổng quát của đường thẳng Δ biết: d. Δ đi qua D(2; 5) và E(3; 1)
e. Δ đi qua G(2; 5) và song song với đường thẳng d: 2x-3y-3 = 0
g. Δ đi qua H(2; 5) và vuông góc với đường thẳng d: x + 3y + 2 = 0
trong mặt phẳng tọa độ Oxy cho điểm A(3;5) và đường thẳng Δ có phương trình:
2x - y + 3 = 0.
a) viết phương trình đường thẳng d đi qua điểm A và song song với Δ
b) viết phương trình đường tròn tâm A tiếp xúc với đường thẳng Δ
c) tìm điểm B trên Δ cách điểm A(3;5) một khoảng cách bằng 5
Trong hệ trục tọa đô Oxy. Cho đường tròn (C):(x-1)2+(y-2)2=5
a/Viết phương trình đường thẳng (d) đi qua gốc tọa đố và tâm của đường tròn (C)
b/Viết phương trình đường thẳng(Δ) đi qua M(1;3) cắt đường tròn (C) theo dây cung AB có độ dài bằng \(3\sqrt{2}\)
làm nhanh giúp e vs ạ
Đường tròn (C) tâm I(1;2) bán kính \(R=\sqrt{5}\)
a.
\(\overrightarrow{OI}=\left(1;2\right)\Rightarrow\) đường thẳng OI nhận (2;-1) là 1 vtpt
Phương trình: \(2\left(x-0\right)-1\left(y-0\right)=0\Leftrightarrow2x-y=0\)
b.
Gọi H là trung điểm AB \(\Rightarrow IH\perp AB\Rightarrow IH=d\left(I;\Delta\right)\)
Áp dụng định lý Pitago:
\(IH=\sqrt{IA^2-AH^2}=\sqrt{R^2-\left(\dfrac{AB}{2}\right)^2}=\dfrac{\sqrt{2}}{2}\)
Phương trình \(\Delta\) qua M có dạng:
\(a\left(x-1\right)+b\left(y-3\right)=0\) với \(a^2+b^2>0\)
\(d\left(I;\Delta\right)=\dfrac{\left|a\left(1-1\right)+b\left(2-3\right)\right|}{\sqrt{a^2+b^2}}=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left|\sqrt{2}b\right|=\sqrt{a^2+b^2}\Leftrightarrow2b^2=a^2+b^2\)
\(\Leftrightarrow a^2=b^2\Leftrightarrow\left[{}\begin{matrix}a=b\\a=-b\end{matrix}\right.\)
Chọn \(a=1\Rightarrow\left[{}\begin{matrix}\left(a;b\right)=\left(1;1\right)\\\left(a;b\right)=\left(1;-1\right)\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}1\left(x-1\right)+1\left(y-3\right)=0\\1\left(x-1\right)-1\left(y-3\right)=0\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Lập phương trình đường thẳng y= ax + b,biế
1. Δ đi qua điểm A(3;-2) và B(2;1)
2. Δ đi qua điểm E(3;3) và song song với đường thẳng d : y=-3x+2 3. ΔΔ đi qua điểm G(1;1) và vuông góc với đường thẳng d: y=-x+1
1: Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}3a+b=-2\\2a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=1-2a=1-2\cdot\left(-3\right)=7\end{matrix}\right.\)
2: Vì (d)//y=-3x+2 nên a=-3
Vậy: y=-3x+b
Thay x=3 và y=3 vào y=-3x+b, ta được:
b-9=3
hay b=12
Đúng 3
Bình luận (2)


















