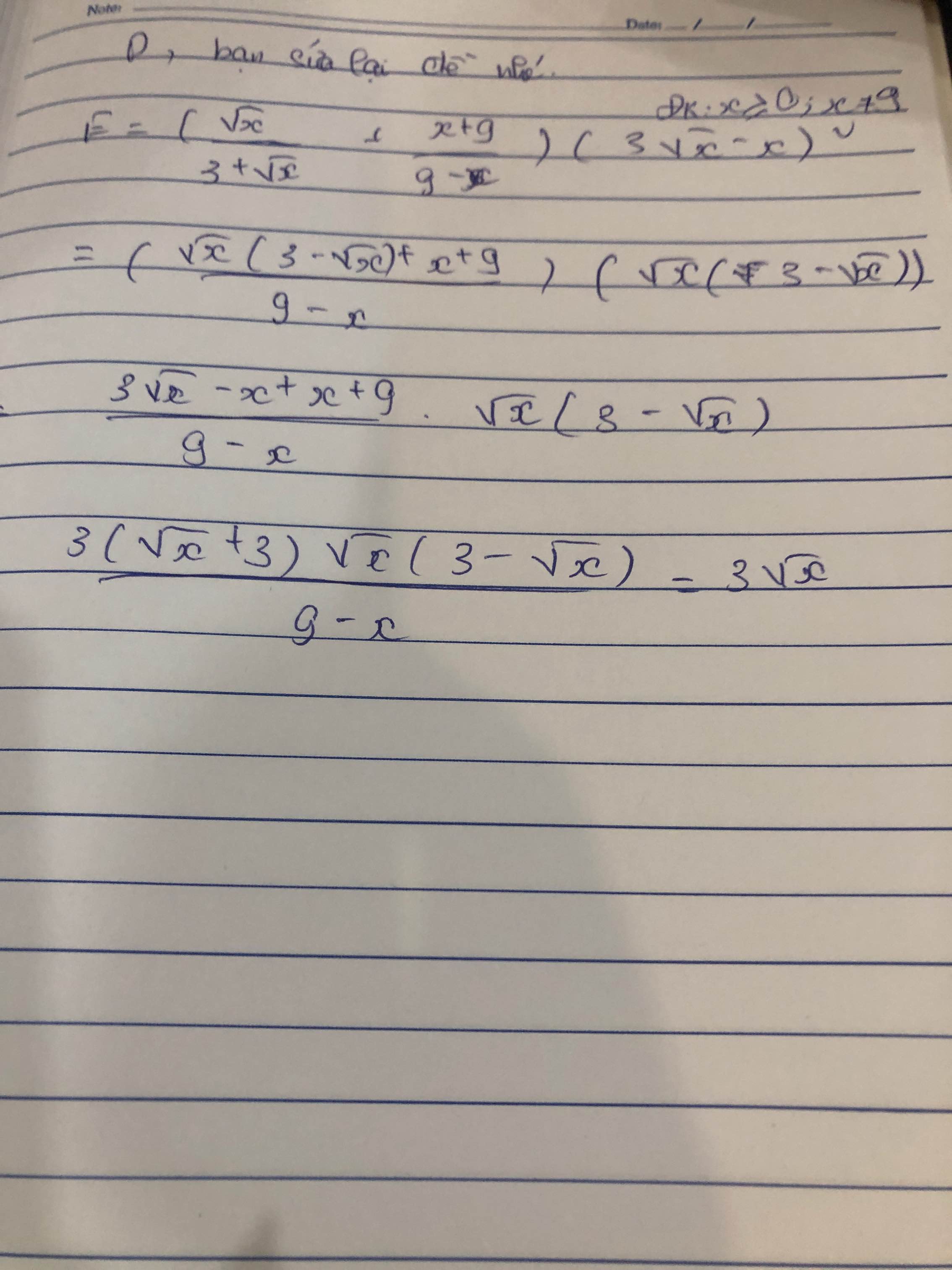\(\sqrt{x^2-9}\left(\frac{3x-1}{x+5}\right)\le x\sqrt{x^2-9}\)

Những câu hỏi liên quan
Bài 1. Tìm điều kiện các BPT sau
a, sqrt{20-x}sqrt{3x-6}+1
b, frac{sqrt{9-x^2}}{x-1}frac{1}{sqrt{x}}+1
c, x+frac{x+1}{sqrt{x-4}}2-frac{2}{x^2-25}
d, sqrt{x}sqrt{-x}
e, 3x+frac{4}{sqrt{x-5}}le9+frac{x}{x-6}
f, frac{x+2}{10+3x^2}ge7+frac{4}{left(3x+9right)^2}
g, frac{sqrt{x+2}}{sqrt{x-2}}+frac{1}{left(x-4right)left(x+6right)}lefrac{3}{sqrt{8-x}}
h, frac{sqrt{x+6}}{left|xright|-sqrt{x+6}}gesqrt{16-2x}
Đọc tiếp
Bài 1. Tìm điều kiện các BPT sau
a, \(\sqrt{20-x}>\sqrt{3x-6}+1\)
b, \(\frac{\sqrt{9-x^2}}{x-1}>\frac{1}{\sqrt{x}}+1\)
c, \(x+\frac{x+1}{\sqrt{x-4}}>2-\frac{2}{x^2-25}\)
d, \(\sqrt{x}>\sqrt{-x}\)
e, \(3x+\frac{4}{\sqrt{x-5}}\le9+\frac{x}{x-6}\)
f, \(\frac{x+2}{10+3x^2}\ge7+\frac{4}{\left(3x+9\right)^2}\)
g, \(\frac{\sqrt{x+2}}{\sqrt{x-2}}+\frac{1}{\left(x-4\right)\left(x+6\right)}\le\frac{3}{\sqrt{8-x}}\)
h, \(\frac{\sqrt{x+6}}{\left|x\right|-\sqrt{x+6}}\ge\sqrt{16-2x}\)
tính tổng các nghiệm thuộc [-5;5] của BPT:
\(\sqrt{x^2-9}\left(\frac{3x-1}{x+5}\right)\le x\sqrt{x^2-9}\)
ĐKXĐ: \(\left[{}\begin{matrix}x\ge3\\x\le-3\end{matrix}\right.\) ; \(x\ne-5\)
- Với \(x=\pm3\) thỏa mãn
- Với \(x\ne\pm3\)
\(\Leftrightarrow\frac{3x-1}{x+5}\le x\Leftrightarrow x-\frac{3x-1}{x+5}\ge0\)
\(\Leftrightarrow\frac{x^2+2x+1}{x+5}\ge0\Leftrightarrow\frac{\left(x+1\right)^2}{x+5}\ge0\)
\(\Rightarrow x>-5\)
Vậy nghiệm của BPT trên \(\left[-5;5\right]\) là: \(\left[{}\begin{matrix}-5< x\le-3\\3\le x\le5\end{matrix}\right.\)
Tính tổng nghiệm hay tổng nghiệm nguyên?
Tổng nghiệm là \(\sum x=5\)
Đúng 0
Bình luận (0)
\(\left(6\right)\dfrac{3\sqrt{x}}{5\sqrt{x}-1}\le-3\)
\(\left(7\right)\dfrac{8\sqrt{x}+8}{6\sqrt{x}+9}>\dfrac{8}{3}\)
\(\left(8\right)\dfrac{\sqrt{x}-2}{2\sqrt{x}-3}< -4\)
\(\left(9\right)\dfrac{4\sqrt{x}+6}{5\sqrt{x}+7}\le-\dfrac{2}{3}\)
\(\left(10\right)\dfrac{6\sqrt{x}-2}{7\sqrt{x}-1}>-6\)
6:ĐKXĐ: x>=0; x<>1/25
BPT=>\(\dfrac{3\sqrt{x}}{5\sqrt{x}-1}+3< =0\)
=>\(\dfrac{3\sqrt{x}+15\sqrt{x}-5}{5\sqrt{x}-1}< =0\)
=>\(\dfrac{18\sqrt{x}-5}{5\sqrt{x}-1}< =0\)
=>\(\dfrac{1}{5}< \sqrt{x}< =\dfrac{5}{18}\)
=>\(\dfrac{1}{25}< x< =\dfrac{25}{324}\)
7:
ĐKXĐ: x>=0
BPT \(\Leftrightarrow\dfrac{\sqrt{x}+1}{2\sqrt{x}+3}>\dfrac{8}{3}:\dfrac{8}{3}=1\)
=>\(\dfrac{\sqrt{x}+1}{2\sqrt{x}+3}-1>=0\)
=>\(\dfrac{\sqrt{x}+1-2\sqrt{x}-3}{2\sqrt{x}+3}>=0\)
=>\(-\sqrt{x}-2>=0\)(vô lý)
8:
ĐKXĐ: x>=0; x<>9/4
BPT \(\Leftrightarrow\dfrac{\sqrt{x}-2}{2\sqrt{x}-3}+4< 0\)
=>\(\dfrac{\sqrt{x}-2+8\sqrt{x}-12}{2\sqrt{x}-3}< 0\)
=>\(\dfrac{9\sqrt{x}-14}{2\sqrt{x}-3}< 0\)
TH1: 9căn x-14>0 và 2căn x-3<0
=>căn x>14/9 và căn x<3/2
=>14/9<căn x<3/2
=>196/81<x<9/4
TH2: 9căn x-14<0 và 2căn x-3>0
=>căn x>3/2 hoặc căn x<14/9
mà 3/2<14/9
nên trường hợp này Loại
9:
ĐKXĐ: x>=0
\(BPT\Leftrightarrow\dfrac{2\sqrt{x}+3}{5\sqrt{x}+7}< =-\dfrac{1}{3}\)
=>\(\dfrac{2\sqrt{x}+3}{5\sqrt{x}+7}+\dfrac{1}{3}< =0\)
=>\(\dfrac{6\sqrt{x}+9+5\sqrt{x}+7}{3\left(5\sqrt{x}+7\right)}< =0\)
=>\(\dfrac{11\sqrt{x}+16}{3\left(5\sqrt{x}+7\right)}< =0\)(vô lý)
10:
ĐKXĐ: x>=0; x<>1/49
\(BPT\Leftrightarrow\dfrac{6\sqrt{x}-2}{7\sqrt{x}-1}+6>0\)
=>\(\dfrac{6\sqrt{x}-2+42\sqrt{x}-6}{7\sqrt{x}-1}>0\)
=>\(\dfrac{48\sqrt{x}-8}{7\sqrt{x}-1}>0\)
=>\(\dfrac{6\sqrt{x}-1}{7\sqrt{x}-1}>0\)
TH1: 6căn x-1>0 và 7căn x-1>0
=>căn x>1/6 và căn x>1/7
=>căn x>1/6
=>x>1/36
TH2: 6căn x-1<0 và 7căn x-1<0
=>căn x<1/6 và căn x<1/7
=>căn x<1/7
=>0<=x<1/49
Đúng 0
Bình luận (1)
Tính tổng các nghiệm nguyên thuộc [-5;5] của bất phương trình \(\sqrt{x^2-9}\left(\frac{3x-1}{x+5}\right)\le x\sqrt{x^2-9}\)
ĐKXĐ: \(\left[{}\begin{matrix}x\ge3\\x\le-3\end{matrix}\right.\); \(x\ne-5\)
Nhận thấy \(x=\pm3\) là 2 nghiệm của BPT đã cho
- Với \(x\ne\pm3\), do \(\sqrt{x^2-9}>0\), chia 2 vế của BPT cho \(\sqrt{x^2-9}\) được:
\(\frac{3x-1}{x+5}\le x\Leftrightarrow\frac{3x-1}{x+5}-x\le0\Leftrightarrow\frac{3x-1-x\left(x+5\right)}{x}\le0\)
\(\Leftrightarrow\frac{-x^2-2x-1}{x}\le0\Leftrightarrow\frac{\left(x+1\right)^2}{x}\ge0\) \(\Rightarrow\left[{}\begin{matrix}x>0\\x=-1\end{matrix}\right.\)
Kết hợp điều kiện xác định ta được: \(\left[{}\begin{matrix}x=-1\\x\ge3\end{matrix}\right.\)
Mà \(x\in\left[-5;5\right]\Rightarrow x=\left\{-3;-1;3;4;5\right\}\)
\(\Rightarrow\sum x=8\)
Đúng 0
Bình luận (0)
\(1.\sqrt{x-1}+\sqrt{x+3}+\sqrt{\left(x-1\right)\left(x^2-3x+5\right)}=4-2x\)
\(2.\frac{x^2}{3+\sqrt{9-x^2}}+\frac{1}{4.\sqrt[2]{9-x^2}}=1\)
1) Đk \(x\ge1\)
Ta có \(\hept{\begin{cases}\sqrt{x-1}\ge0\\\sqrt{x+3}\ge\sqrt{1+3}=2\\\sqrt{\left(x-1\right)\left(x^2-3x+5\right)}\ge0\end{cases}\Rightarrow VT\ge2}\)
Mà \(4-2x\le2\Rightarrow VT\ge VP\)
Dấu = xảy ra <=> x=1
Vậy ...^^
Đúng 0
Bình luận (0)
Ma tai sao \(\sqrt{x-1}+\sqrt{x+3}\ge2\)
Đúng 0
Bình luận (0)
=>
Đk x > 1
Ta có { x - 1 ==>0
x+3 >1+3=^2 =>:Vt>2
x-1 . (x2 - 3x+5) >0
Theo kết luận là
...........
Đúng 0
Bình luận (0)
Rút gọn biểu thức :
a) A = 4\(\sqrt{x}\)- \(\frac{\left(x+6\sqrt{x}+9\right)\left(\sqrt{x}-3\right)}{x-9}\)với 0 ≤ x ≠ 9 ;
b) B = \(\frac{\sqrt{9x^2+12x+4}}{3x+2}\)với x ≠ \(-\frac{2}{3}\)
Lời giải:
a) \(A=4\sqrt{x}-\frac{(\sqrt{x}+3)^2(\sqrt{x}-3)}{x-9}=4\sqrt{x}-\frac{(\sqrt{x}+3)(x-9)}{x-9}=4\sqrt{x}-(\sqrt{x}+3)\)
\(=3\sqrt{x}-3\)
b)
\(B=\frac{\sqrt{9x^2+12x+4}}{3x+2}=\frac{\sqrt{(3x)^2+2.3x.2+2^2}}{3x+2}=\frac{\sqrt{(3x+2)^2}}{3x+2}=\frac{|3x+2|}{3x+2}\)
\(B=1\) nếu $x>\frac{-2}{3}$
$B=-1$ nếu $x< \frac{-2}{3}$
Đúng 0
Bình luận (0)
Điều kiện: $ - frac{1}{3} le x le 6$
Ta nhẩm thấy x 5 là nghiệm của PT, thêm bớt và trục căn thức ta có:
Phương trình $ Leftrightarrow left( {sqrt {3x + 1} - 4} right) - left( {sqrt {6 - x} - 1} right) + left( {3{x^2} - 14x - 5} right) 0$
$ Leftrightarrow frac{{3left( {x - 5} right)}}{{sqrt {3x + 1} + 4}} + frac{{x - 5}}{{sqrt {6 - x} + 1}} + left( {3x + 1} right)left( {x - 5} right) 0$
$ Leftrightarrow left( {x - 5} right)left[ {frac{3}{{sqrt {3x + 1} + 4}} + frac{1}{{sqrt {6 - x} +...
Đọc tiếp
Điều kiện: $ - \frac{1}{3} \le x \le 6$
Ta nhẩm thấy x = 5 là nghiệm của PT, thêm bớt và trục căn thức ta có:
Phương trình $ \Leftrightarrow \left( {\sqrt {3x + 1} - 4} \right) - \left( {\sqrt {6 - x} - 1} \right) + \left( {3{x^2} - 14x - 5} \right) = 0$
$ \Leftrightarrow \frac{{3\left( {x - 5} \right)}}{{\sqrt {3x + 1} + 4}} + \frac{{x - 5}}{{\sqrt {6 - x} + 1}} + \left( {3x + 1} \right)\left( {x - 5} \right) = 0$
$ \Leftrightarrow \left( {x - 5} \right)\left[ {\frac{3}{{\sqrt {3x + 1} + 4}} + \frac{1}{{\sqrt {6 - x} + 1}} + \left( {3x + 1} \right)} \right] = 0 \Leftrightarrow \left( {x - 5} \right)g\left( x \right) = 0$
Với điều kiện trên ta thấy g(x) > 0 vậy x = 5 là nghiệm của PT.
ta có Pfrac{x^2}{xsqrt{y+3}}+frac{y^2}{ysqrt{z+3}}+frac{z^2}{zsqrt{x+3}}gefrac{left(x+y+zright)^2}{xsqrt{y+3}+ysqrt{z+3}+zsqrt{x+3}}mà left(xsqrt{y+3}+...right)^2leleft(x+y+zright)left(xy+yz+zx+3x+3y+3zright)le3left(9+3right)36 ( vì xy+yz+zx3)xsqrt{y+3}+...le6Rightarrow Pgefrac{9}{6}frac{3}{2}dấu xảy ra xyz1
Đọc tiếp
ta có P=\(\frac{x^2}{x\sqrt{y+3}}+\frac{y^2}{y\sqrt{z+3}}+\frac{z^2}{z\sqrt{x+3}}\ge\frac{\left(x+y+z\right)^2}{x\sqrt{y+3}+y\sqrt{z+3}+z\sqrt{x+3}}\)
mà \(\left(x\sqrt{y+3}+...\right)^2\le\left(x+y+z\right)\left(xy+yz+zx+3x+3y+3z\right)\le3\left(9+3\right)=36\) ( vì xy+yz+zx<=3)
=>\(x\sqrt{y+3}+...\le6\Rightarrow P\ge\frac{9}{6}=\frac{3}{2}\)
dấu = xảy ra <=> x=y=z=1
Rút gọn các biểu thức sau:
\(D=\left(\frac{5\sqrt{x-6}}{x-9}-\frac{2}{\sqrt{x}+3}\right):\left(1+\frac{6}{x-9}\right)\)
\(E=\left(\frac{\sqrt{x}}{3+\sqrt{x}}+\frac{9+x}{9-x}\right).\left(3\sqrt{x}-x\right)\)