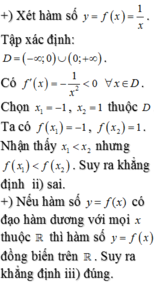nếu cho x không âm và\(\sqrt{x}\)=3 thì x2 bằng

Những câu hỏi liên quan
cho các số thực x, y ,z không âm thoả mãn : x2+y2+z2=1 .
Tìm giá tri nhỏ nhất và giá tri lớn nhất của \(A=\sqrt{x+y}+\sqrt{y+z}+\sqrt{z+x}\)
\(A\le\sqrt{3\left(x+y+y+z+z+x\right)}=\sqrt{6\left(x+y+z\right)}\le\sqrt{6.\sqrt{3\left(x^2+y^2+z^2\right)}}=\sqrt{6\sqrt{3}}\)
\(A_{max}=\sqrt{6\sqrt{3}}\) khi \(x=y=z=\dfrac{1}{\sqrt{3}}\)
Do \(x^2+y^2+z^2=1\Rightarrow0\le x;y;z\le1\)
\(\Rightarrow\left\{{}\begin{matrix}x^2\le x\\y^2\le y\\z^2\le z\end{matrix}\right.\) \(\Rightarrow x+y+z\ge x^2+y^2+z^2=1\)
\(A^2=2\left(x+y+z\right)+2\sqrt{\left(x+y\right)\left(x+z\right)}+2\sqrt{\left(x+y\right)\left(y+z\right)}+2\sqrt{\left(y+z\right)\left(z+x\right)}\)
\(A^2=2\left(x+y+z\right)+2\sqrt{x^2+xy+yz+zx}+2\sqrt{y^2+xy+yz+zx}+2\sqrt{z^2+xy+yz+zx}\)
\(A^2\ge2\left(x+y+z\right)+2\sqrt{x^2}+2\sqrt{y^2}+2\sqrt{z^2}=4\left(x+y+z\right)\ge4\)
\(\Rightarrow A\ge2\)
\(A_{min}=2\) khi \(\left(x;y;z\right)=\left(0;0;1\right)\) và các hoán vị
Đúng 0
Bình luận (0)
cho x,y,z là 3 số dương và không đồng thời bằng nhau. Chứng minh rằng: Nếu\(\sqrt{x}+\frac{1}{\sqrt{y}}=\sqrt{y}+\frac{1}{\sqrt{z}}=\sqrt{z}+\frac{1}{\sqrt{z}}\) thì xyz=1
n+m = số chẵn mà nếu nó cộng chính nó x 2 sẽ bằng n hay trừ chính nó x 3
n-m = n x 1,5 = m x 0,6
n không phải số dương hoặc không phải số lẻ
m chỉ có thể là số chẵn hoặc số âm
Biết rằng nếu n + số chẵn lớn hơn 98 thì n không phải số âm
chứng minh n x m sẽ là một số lẻ nếu m là số âm và nếu n là số dương thì là số chẵn
À lộn n+m = số chẵn mà nếu số đó cộng nó nhân hai bằng n còn nếu nó trừ nó nhân ba bằng m
Đúng 0
Bình luận (0)
Xét các khẳng định sau i) Nếu hàm số yf(x) có đạo hàm dương với mọi x thuộc tập số D thì
f
x
1
f
x
2
∀
x
1
,
x
2
∈
D
,
x
1
x
2
ii) Nếu hàm số yf(x) có đạo hàm âm với...
Đọc tiếp
Xét các khẳng định sau
i) Nếu hàm số y=f(x) có đạo hàm dương với mọi x thuộc tập số D thì f x 1 < f x 2 ∀ x 1 , x 2 ∈ D , x 1 < x 2
ii) Nếu hàm số y=f(x) có đạo hàm âm với mọi x thuộc tập số D thì f x 1 > f x 2 ∀ x 1 , x 2 ∈ D , x 1 < x 2
iii) Nếu hàm số y=f(x) có đạo hàm dương với mọi x thuộc R thì f x 1 < f x 2 ∀ x 1 , x 2 ∈ R , x 1 < x 2
iv) Nếu hàm số y=f(x) có đạo hàm âm với mọi x thuộc R thì f x 1 > f x 2 ∀ x 1 , x 2 ∈ R , x 1 < x 2
Số khẳng định đúng là
A. 1
B. 2
C. 3
D. 4
Cho x và y là hai đại lượng tỉ lệ nghịch và nếu y1 = 9; y2 = 8 thì 3.x1+6.x2= (1/13)^(-1).
Vậy nếu x= -12 thì y bằng bao nhiêu?
Cho x, y không âm và x+y ≤1. Tìm GTLN của \(A=\sqrt{1+4x^2}+\sqrt{1+4y^2}+3\sqrt{x}+3\sqrt{y}\)
Mọi người giúp em với, xin cảm ơn ạ.
CMR nếu tổng các số x, y, z không âm thì : x3+ y3+ z3 lớn hơn hoặc bằng 3xyz
chết mk nhìn nhầm , tổng ko âm chứ ko phải x,y,z ko âm
Đúng 1
Bình luận (0)
Vì x + y + z không âm nên x,y,z không âm
Áp dụng BĐT AM - GM:
\(x^3+y^3+z^3\ge3\sqrt[3]{\left(xyz\right)^3}=3xyz\)
Đúng 1
Bình luận (0)
a) Tìm giá trị của x2 với x lần lượt bằng 2; 3; 4; 5; 10.b) Tìm số thực không âm x với x2 lần lượt bằng 4; 9; 16; 25; 100.
Đọc tiếp
a) Tìm giá trị của x2 với x lần lượt bằng 2; 3; 4; 5; 10.
b) Tìm số thực không âm x với x2 lần lượt bằng 4; 9; 16; 25; 100.
a) x = 2, ta được x2 = 4;
x =3, ta được x2 = 9;
x = 4, ta được x2 = 16;
x =5, ta được x2 = 25;
x = 10, ta được x2 = 100.
b) x2 = 4, ta được x = 2;
x2 = 9, ta được x = 3;
x2 = 16, ta được x = 4;
x2 = 25, ta được x = 5;
x2 = 100, ta được x = 10.
Đúng 0
Bình luận (0)
Cho x2 + y2 = 1
Giải : \(2\sqrt{3}x+4\sqrt{3}xy+4y^2-2y-5=0\)
Cho mình hỏi là nếu như mình đặt x = sina và y = cosa