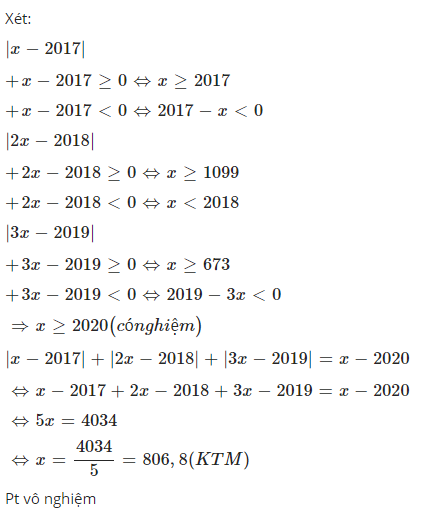\(\Leftrightarrow\left(2x-3\right)\left(2x-\dfrac{7}{2}\right)\left(2x-\dfrac{5}{2}\right)=0\)

\(\Leftrightarrow x\in\left\{\dfrac{3}{2};\dfrac{7}{4};\dfrac{5}{4}\right\}\)

x = 4

\(\Leftrightarrow\left(2x-7\right)^{2017}\left[\left(2x-7\right)^2-1\right]=0\)

=>(2x-7)(2x-6)(2x-8)=0

hay \(x\in\left\{3;\dfrac{7}{2};4\right\}\)

Đi mà hỏi Ông Thắng 

Tham khảo :

Nhận thấy vế trái luôn dương nên \(x-2020\ge0\Leftrightarrow x\ge2020\)

Với \(x\ge2020\Rightarrow\left\{{}\begin{matrix}x-2017\ge0\\2x-2018\ge0\\3x-2019\ge0\end{matrix}\right.\)

PT trở thành: \(x-2017+2x-2018+3x-2019=x-2020\)

Hay kết hợp với điều kiện \(x=\dfrac{4034}{5}\) suy ra PT đã cho vô nghiệm 

\(\left|x-2017\right|+\left|2x-2018\right|+\left|3x-2019\right|=x-2020\)

\(ĐK:x\ge2020\)

\(\Leftrightarrow x-2017+2x-2018+3x-2019=x-2020\)

\(\Leftrightarrow5x=4034\)

\(\Leftrightarrow x=806,8\left(tm\right)\)

Vậy \(S=\left\{806,8\right\}\)

Đặt \(2017-x=m,2019-x=n\)

\(\rightarrow m+n=2x-4036\)

Phương trình ban đầu trở thành :

\(m^3+n^3=\left(m+n\right)^3\)

\(\rightarrow3mn.\left(m+n\right)^3=0\)

\(\rightarrow\left(2017-x\right)\left(2019-x\right)\left(2x-4036\right)=0\)

\(\rightarrow\left[{}\begin{matrix}x=2017\\x=2018\\x=2019\end{matrix}\right.\)

Vậy \(S=\left\{2017;2018;2019\right\}\)

(2017-X)³+(2019-X)³+(2X-4036)³=0

<=>(2017-x).(2018-x).(2019-x)=0

<=>x=2017

x=2018

x=2019

#YQ

TH1: 2x² +2017=2019

2x² =2019-2017

2x² =2

x² =2 : 2

x² =1

=>x=1

TH2: 2x² +2017= -2019

tự tính tiếp nha

\(\left|2x^2+2017\right|=2019\)

\(\Rightarrow\orbr{\begin{cases}2x^2+2017=2019\\2x^2+2017=-2019\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}2x^2=2\\2x^2=-4036\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}x^2=1\\x^2=-2018\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}x=\pm1\\x\in\varnothing\end{cases}}\)

vậy_

Tìm  x , biết : 

| 2x^2 + 2017 | = 2019 

<=> 2x^2 + 2017 = 2019 hoặc 2x^2 + 2017 = -2019 

<=> 2x^2 = 2 hoặc 2x^2 = -4036 

<=> x^2 = 1 hoặc x^2 = -2018 

<=> x = 1 hoặc x = \(\varnothing\)

Vậy x = 1