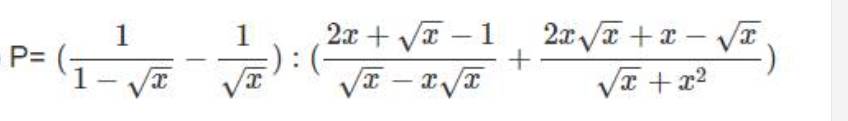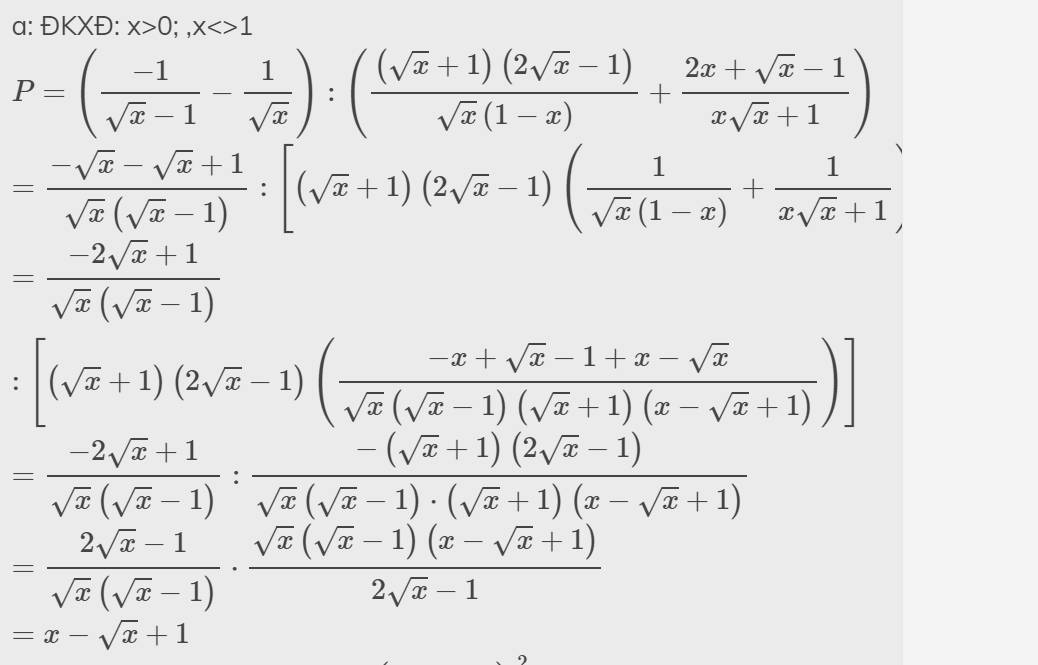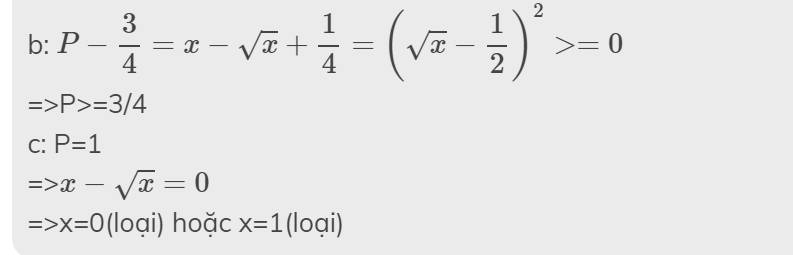a: ĐKXĐ: x>=0; x<>4

\(Q=\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)+2\sqrt{x}\left(\sqrt{x}+2\right)-3x-4}{x-4}\cdot\dfrac{\sqrt{x}-2+2}{2}\)

\(=\dfrac{x-2\sqrt{x}+2x+4\sqrt{x}-3x-4}{x-4}\cdot\dfrac{\sqrt{x}}{2}\)

\(=\dfrac{2\sqrt{x}-4}{x-4}\cdot\dfrac{\sqrt{x}}{2}=\dfrac{\sqrt{x}}{\sqrt{x}+2}\)

b: \(M=P\cdot Q=\dfrac{\sqrt{x}}{\sqrt{x}+2}\cdot\dfrac{1-5\sqrt{x}}{\sqrt{x}+1}=\dfrac{\sqrt{x}\left(1-5\sqrt{x}\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}+1\right)}\)

\(M\left(M-1\right)=\dfrac{\sqrt{x}\left(1-5\sqrt{x}\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}-5x-x-3\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}+1\right)}\)

\(=\dfrac{\sqrt{x}\left(1-5\sqrt{x}\right)\left(-6x-2\sqrt{x}-2\right)}{\left(\sqrt{x}+2\right)^2\cdot\left(\sqrt{x}+1\right)^2}\)

\(=\dfrac{\sqrt{x}\left(5\sqrt{x}-1\right)\left(6x+2\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)^2\left(\sqrt{x}+1\right)^2}\)

TH1: M>=căn M

=>M^2>=M

=>M^2-M>=0

=>5*căn x-1>=0

=>x>=1/25 và x<>4

TH2: M<căn M

=>5căn x-1<0

=>x<1/25

Kết hợp ĐKXĐ, ta được: 0<=x<1/25

1: \(B=\dfrac{\sqrt{x}-1}{\sqrt{x}-2}-\dfrac{5\sqrt{x}-8}{\sqrt{x}\left(\sqrt{x}-2\right)}\)

\(=\dfrac{x-\sqrt{x}-5\sqrt{x}+8}{\sqrt{x}\left(\sqrt{x}-2\right)}=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}-4\right)}{\sqrt{x}\left(\sqrt{x}-2\right)}\)

\(=\dfrac{\sqrt{x}-4}{\sqrt{x}}\)

2: \(P=A\cdot B=\dfrac{x+\sqrt{x}+1}{\sqrt{x}}\)

\(\Leftrightarrow P-2=\dfrac{x-\sqrt{x}+1}{\sqrt{x}}>0\)

=>P>2

\(a,B=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{2}{\sqrt{x}+3}-\dfrac{9\sqrt{x}-3}{x+\sqrt{x}-6}\left(x>0;x\ne6\right)\\ =\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{2}{\sqrt{x}+3}-\dfrac{9\sqrt{x}-3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\\ =\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}+\dfrac{2\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}-\dfrac{9\sqrt{x}-3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\\ =\dfrac{x+3\sqrt{x}+\sqrt{x}+3+2\sqrt{x}-4-9\sqrt{x}+3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\\ =\dfrac{x-3\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\\\)

\(=\dfrac{x-\sqrt{x}-2\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\\ =\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)-2\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\\ =\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\\ =\dfrac{\sqrt{x}-1}{\sqrt{x}+3}\)

`b,` Tớ tính mãi ko ra, xl cậu nha=')

\(P=\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+3}{x-9}\left(ĐKXĐ:x\ge0;x\ne9\right)\)

\(=\dfrac{2\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}-\dfrac{3x+3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)

\(=\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}-3x-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)

\(=\dfrac{-3\sqrt{x}-3}{x-9}\)

\(b,M=P:Q\)

\(=\dfrac{-3\sqrt{x}-3}{x-9}:\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)

\(=\dfrac{-3\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}\)

\(=\dfrac{-3}{\sqrt{x}+3}\)

Ta thấy: \(\sqrt{x}\ge0\forall x\)

\(\Rightarrow\sqrt{x}+3\ge3\forall x\)

\(\Rightarrow\dfrac{1}{\sqrt{x}+3}\le\dfrac{1}{3}\forall x\)

\(\Rightarrow\dfrac{-3}{\sqrt{x}+3}\ge\dfrac{-3}{3}=-1\)

hay \(M\ge-1\)

#Toru

\(A=\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}-1}{2}\left(dkxd:x\ge0;x\ne1\right)\)

\(=\left[\dfrac{x+2}{\left(\sqrt{x}\right)^3-1}+\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{1}{\sqrt{x}-1}\right]\cdot\dfrac{2}{\sqrt{x}-1}\)

\(=\left[\dfrac{x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right]\cdot\dfrac{2}{\sqrt{x}-1}\)

\(=\dfrac{x+2+x-\sqrt{x}-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}-1}\)

\(=\dfrac{\left(x-2\sqrt{x}+1\right)\cdot2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)\cdot\left(\sqrt{x}-1\right)}\)

\(=\dfrac{\left(\sqrt{x}-1\right)^2\cdot2}{\left(\sqrt{x}-1\right)^2\cdot\left(x+\sqrt{x}+1\right)}\)

\(=\dfrac{2}{x+\sqrt{x}+1}\)

Xét: \(A-2=\dfrac{2}{x+\sqrt{x}+1}-2\)

\(=\dfrac{2}{x+\sqrt{x}+1}-\dfrac{2\left(x+\sqrt{x}+1\right)}{x+\sqrt{x}+1}\)

\(=\dfrac{2-2x-2\sqrt{x}-2}{x+\sqrt{x}+1}\)

\(=\dfrac{-2x-2\sqrt{x}}{x+\sqrt{x}+1}\)

\(=\dfrac{-2\left(x+\sqrt{x}\right)}{x+\sqrt{x}+1}\)

Với \(x\ge0;x\ne1\Leftrightarrow\left\{{}\begin{matrix}x+\sqrt{x}\ge0\\x+\sqrt{x}+1>0\end{matrix}\right.\)

\(\Leftrightarrow\dfrac{x+\sqrt{x}}{x+\sqrt{x}+1}\ge0\)

\(\Leftrightarrow\dfrac{-2\left(x+\sqrt{x}\right)}{x+\sqrt{x}+1}\le0\)

\(\Rightarrow A-2\le0\Leftrightarrow A\le2\)

Vậy: \(A\le2\).

a) \(P=\left(\dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\right).\left(\dfrac{1}{2\sqrt{x}}-\dfrac{\sqrt{x}}{2}\right)^2\left(đk:x>0\right)\)

\(=\dfrac{\left(\sqrt{x}-1\right)^2-\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\left(\dfrac{1-x}{2\sqrt{x}}\right)^2=\dfrac{x-2\sqrt{x}+1-x-2\sqrt{x}-1}{x-1}.\dfrac{\left(x-1\right)^2}{4x}=\dfrac{-4\sqrt{x}\left(x-1\right)}{4x}=\dfrac{1-x}{\sqrt{x}}\)

b) \(P-\left(-2\sqrt{x}\right)=\dfrac{1-x}{\sqrt{x}}+2\sqrt{x}=\dfrac{1-x+2x}{\sqrt{x}}=\dfrac{1+x}{\sqrt{x}}>0\)

\(\Rightarrow P>-2\sqrt{x}\)

a, ĐK: \(x\ge0;x\ne1\)

\(P=\left(\dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\right)\left(\dfrac{1}{2\sqrt{x}}-\dfrac{\sqrt{x}}{2}\right)^2\)

\(=\dfrac{\left(\sqrt{x}-1\right)^2-\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}.\dfrac{\left(2-2x\right)^2}{16x}\)

\(=\dfrac{-4\sqrt{x}}{x-1}.\dfrac{4\left(x-1\right)^2}{16x}\)

\(=-\dfrac{x-1}{\sqrt{x}}\)

a: Ta có: \(P=\left(\dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\right)\cdot\left(\dfrac{1}{2\sqrt{x}}-\dfrac{\sqrt{x}}{2}\right)^2\)

\(=\dfrac{x-2\sqrt{x}+1-x-2\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)^2\cdot\left(\sqrt{x}+1\right)^2}{4x}\)

\(=\dfrac{-4\sqrt{x}\left(x-1\right)}{4x}\)

\(=\dfrac{-x+1}{\sqrt{x}}\)

câu 2 rút gọn A và tìm các giá trị nguyên của x để A nhận giá trị âm

1) So sánh:

N = \(\dfrac{5+\sqrt{5}}{\sqrt{5}+1}-\sqrt{6-2\sqrt{5}}\)

\(=\dfrac{\sqrt{5}\left(\sqrt{5}+1\right)}{\sqrt{5}+1}-\sqrt{\left(\sqrt{5}-1\right)^2}\)

\(=\sqrt{5}-\left(\sqrt{5}-1\right)=1\)

M = \(\sqrt{18}-\sqrt{8}\)

\(=3\sqrt{2}-2\sqrt{2}\)

\(=\sqrt{2}\)

Ta có: \(1=\sqrt{1}\)

Mà 1 < 2

\(\Rightarrow\sqrt{1}< \sqrt{2}\)

Hay 1 \(< \sqrt{2}\)

Vậy N < M
 

2) Với \(x>0;x\ne4;x\ne9\), ta có:

A = \(\left(\dfrac{\sqrt{x}}{3+\sqrt{x}}+\dfrac{2x}{9-x}\right):\left(\dfrac{x-4}{x-3\sqrt{x}}-\dfrac{2}{\sqrt{x}}\right)\)

\(=\left[\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}-\dfrac{2x}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\right]:\left[\dfrac{x-4}{\sqrt{x}\left(\sqrt{x}-3\right)}-\dfrac{2\left(\sqrt{x}-3\right)}{\sqrt{x}\left(\sqrt{x}-3\right)}\right]\)

\(=\dfrac{x-3\sqrt{x}-2x}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}:\dfrac{x-4-2\sqrt{x}+6}{\sqrt{x}\left(\sqrt{x-3}\right)}\)

\(=\dfrac{-x-3\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}.\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{x-2\sqrt{x}+2}\)

\(=\dfrac{-\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}.\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{x-2\sqrt{x}+2}\)

\(=\dfrac{-x}{x-2\sqrt{x}+2}\)

Sửa đề: