chứng minh tam giác ABC là tam giác vuông nếu 20AB=15AC=12BC

Những câu hỏi liên quan
Chứng minh tam giác ABC là tam giác vuông nếu biết 20AB=15AC=12BC
Chứng minh tam giác ABC là tam giác vuông trong các trường hợp sau:
1) AB = 3x, AC = 4x, BC = 5x (x > 0).
2) AB/3 = AC/4 = BC/5
3) 20AB = 15AC = 12BC
chứng minh tam giác abc là tam giác vuông biết: a)ab=5x,ac=12x,bc=13x
b)20ab=15ac=12bc
a) Xét \(\Delta ABC\) có:
\(AB^2+AC^2=\left(5x\right)^2+\left(12x\right)^2\)
=> \(AB^2+AC^2=25x^2+144x^2\)
=> \(AB^2+AC^2=169x^2\) (1).
\(BC^2=\left(13x\right)^2\)
=> \(BC^2=169x^2\) (2).
Từ (1) và (2) => \(AB^2+AC^2=BC^2\left(=169x^2\right).\)
=> \(\Delta ABC\) vuông tại \(A\) (định lí Py - ta - go đảo) (đpcm).
Chúc bạn học tốt!
Chứng minh tam giác ABC là tam giác vuông trong các trường hợp sau:
1) AB=3x,AC=4x,BC=5x (x>0)
2) \(\frac{AB}{3}\)=\(\frac{AC}{4}\)=\(\frac{BC}{5}\)
3) 20AB=15AC=12BC
1.
\(AB^2+AC^2=BC^2\\ hay\left(3x\right)^2+\left(4x\right)^2=\left(5x\right)^2\\\Leftrightarrow 9x^2+16x^2=25x^2\\\Leftrightarrow 25x^2=25x^2\left(tm\right)\)
Vậy trong trường hợp này \(\Delta ABC\) là tam giác vuông.
2.
\(\frac{AB}{3}=\frac{AC}{4}=\frac{BC}{5}=a\\ \Rightarrow\left\{{}\begin{matrix}AB=3a\\AC=4a\\BC=5a\end{matrix}\right.\)
Ta có: \(AB^2+AC^2=9a^2+16a^2=25a^2=BC^2=\left(5a\right)^2=25a^2\left(tm\right)\)
Vậy trong TH này tam giác ABC là tam giác vuông (Theo đl PTG đảo)
3.
\(20AB=15AC=12BC\\\Rightarrow \frac{20AB}{60}=\frac{15AC}{60}=\frac{12BC}{60}\\ \Rightarrow\frac{AB}{3}=\frac{AC}{4}=\frac{BC}{5}=a\)
\(\Rightarrow\left\{{}\begin{matrix}AB=3a\\AC=4a\\BC=5a\end{matrix}\right.\)
Ta có: \(AB^2+AC^2=9a^2+16a^2=25a^2=BC^2=\left(5a\right)^2=25a^2\left(tm\right)\)
Vậy trong TH này tam giác ABC là tam giác vuông (Theo định lí Py-ta-go đảo)
Chứng minh tam giác ABC là tam giác vuông trong các trường hợp sau:
a) AB = 3x, AC = 4x, BC = 5x (x > 0)
b) AB = 5x, AC = 12x, BC = 13x (x > 0)
c) AB = 40x, AC = 41x, BC = 9x (x > 0)
d) 20AB = 15AC = 12BC
e) 65AB = 156AC = 60BC
a)Ta có:
\(AB^2+AC^2= \left(3x\right)^2+\left(4x\right)^2=9x^2+16x^2=25x^2=\left(5x\right)^2=BC^2\)Theo định lí Pytago đảo, △ABC vuông tại A (đpcm)
b)Ta có:
\(AB^2+AC^2=\left(5x\right)^2+\left(12x\right)^2=25x^2+144x^2=169x^2=\left(13x\right)^2=BC^2\)
Theo định lí Pytago đảo, △ABC vuông tại A (đpcm)
c)Ta có:
\(AB^2+BC^2=\left(40x\right)^2+\left(9x\right)^2=1600x^2+81x^2=1681x^2=\left(41x\right)^2=AC^2\)
Theo định lí Pytago đảo, △ABC vuông tại B (đpcm)
d)Ta có:
\(20AB=15AC=12BC\Rightarrow\frac{20AB}{60}=\frac{15AC}{60}=\frac{12BC}{60}\Rightarrow\frac{AB}{3}=\frac{AC}{4}=\frac{BC}{5}=k\)\(\Rightarrow\left\{{}\begin{matrix}AB=3k\\AC=4k\\BC=5k\end{matrix}\right.\)
\(\Rightarrow AB^2+AC^2=\left(3k\right)^2+\left(4k\right)^2=9k^2+16k^2=25k^2=\left(5k\right)^2=BC^2\)
Theo định lí Pytago đảo, △ABC vuông tại A (đpcm)
e)Ta có:
\(65AB=156AC=60BC\Rightarrow\frac{65AB}{780}=\frac{156AC}{780}=\frac{60BC}{780}\Rightarrow\frac{AB}{12}=\frac{AC}{5}=\frac{BC}{13}=k\)\(\Rightarrow\left\{{}\begin{matrix}AB=12k\\AC=5k\\BC=13k\end{matrix}\right.\)
\(\Rightarrow AB^2+AC^2=\left(12k\right)^2+\left(5k\right)^2=144k^2+25k^2=169k^2=\left(13k\right)^2=BC^2\)
Theo định lí Pytago đảo, △ABC vuông tại A (đpcm)
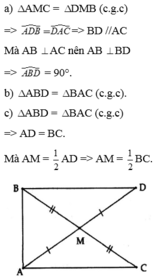
Cho tam giác ABC vuông tại A, trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD MA.a) Tính
A
B
D
^
b) Chứng minh
∆
A
B
D
∆
B
A
C
.
c) Chứng minh
A
M
1
2
B
C
Đọc tiếp
Cho tam giác ABC vuông tại A, trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a) Tính A B D ^
b) Chứng minh ∆ A B D = ∆ B A C .
c) Chứng minh A M = 1 2 B C
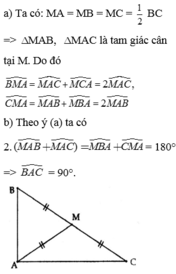
Cho tam giác ABC, trung tuyến
A
M
1
2
B
C
.
a) Chứng minh
B
M
A
^
2
M
A
C
^
và
C
M
A
^
2...
Đọc tiếp
Cho tam giác ABC, trung tuyến A M = 1 2 B C .
a) Chứng minh B M A ^ = 2 M A C ^ và C M A ^ = 2 M A B ^ .
b) Tính B A C ^ ?
Cho tam giác ABC vuông tại A, AH là đường cao.
a) Chứng minh: tam giác HBA đồng dạng với tam giác ABC
b) Chứng minh: tam giác HBA đồng dạng với tam giác HAC. Từ đó suy ra: AH.AH=BH.HC
c) Kẻ HD vuông góc với AB và HE vuông góc với AC. Chứng minh: tam giác AED đồng dạng với tam giác ABC
d) Nếu AB.AC=4AD.AE thì tam giác ABC là tam giác gì?
Mình đã giải xong câu a, b, c. Nhờ các bạn và quý thầy cô giải giúp câu d. Chỉ cần tóm tắt lời giải thôi cũng được ạ.
Đúng 0
Bình luận (0)
d) SADE = 1/2.AD.AE ; SABC = 1/2.AB.AC => SADE / SABC = AD.AE/AB.AC =1/4 (1)
Do tg ADE đồng dạng tg ABC => SADE / SABC = (DE/BC)2 = (AH/BC)2 (2)
Từ (1) và (2) => AH/BC = 1/2 hay AH = !/2 BC. Vậy AH là đường trung tuyến tg ABC, mà AH là đường cao => tg ABC cân tại A
Đúng 0
Bình luận (0)
Vẽ tam giác ABC cân tại A kẻ K vuông góc vưới BC
a,Chứng minh KB=KC
b, từ K kẻ D vuông góc AB ( D thuộc AB),từ K kẻ E vuông góc với AC (E thuộc AC) chứng minh tam giác DEK là tam giác cân
c, Nếu tam giác ABC =120độ thì tam giác KED là tam giác gì ? vì sao ?
MN giúp mk với ạ ! mk cần gấp lắm mk xin cảm ơn ạ:>
a: Ta có: ΔABC cân tại A
mà AK là đường cao
nên K là trung điểm của BC
hay KB=KC
b: Xét ΔADK vuông tại D và ΔAEK vuông tại E có
AK chung
\(\widehat{DAK}=\widehat{EAK}\)
Do đó:ΔADK=ΔAEK
Suy ra: KD=KE
hay ΔKDE cân tại K
Đúng 0
Bình luận (0)