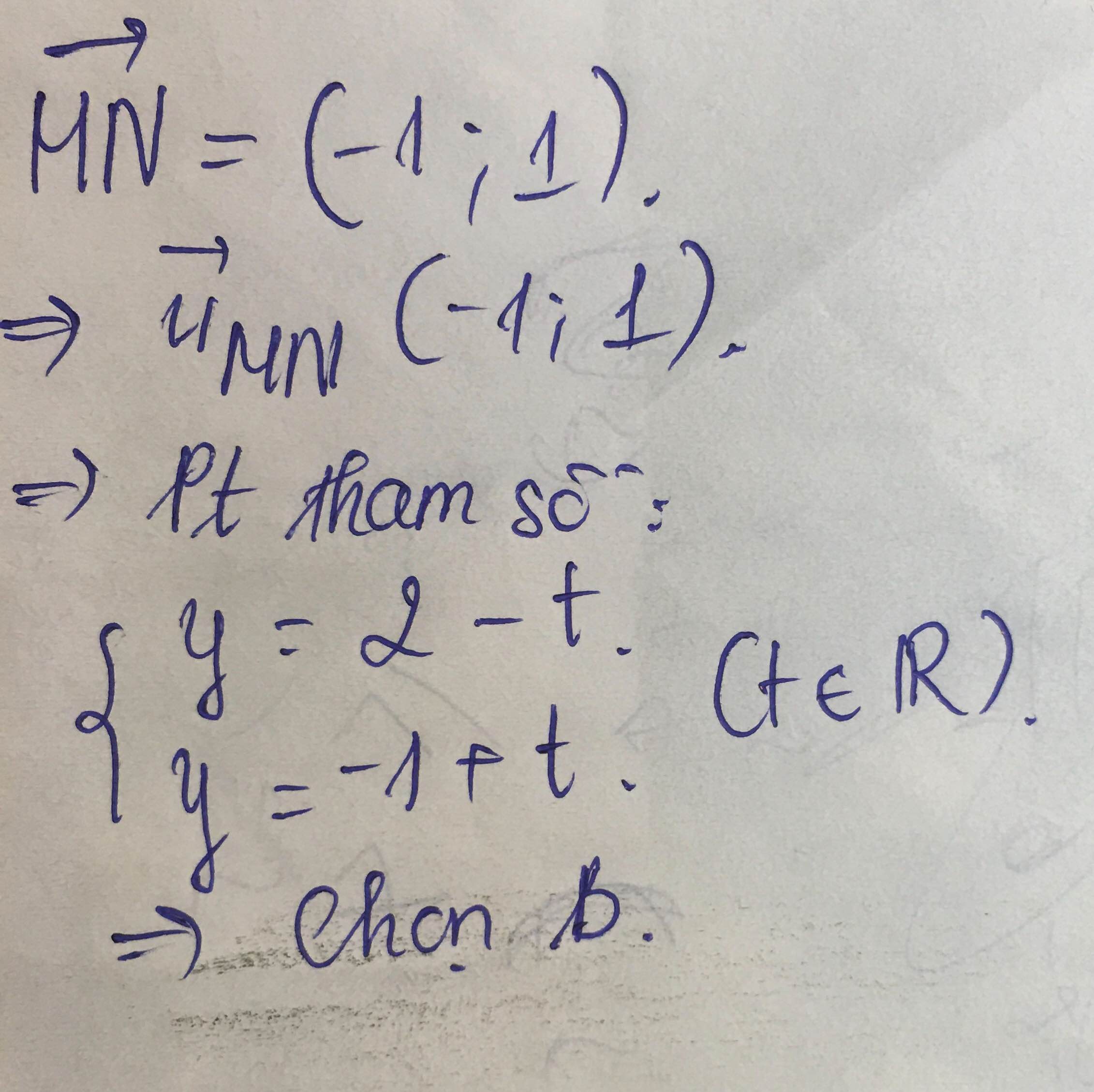Tìm tất cả giá trị của tham số m để khoảng cách từ giao điểm của hai đường thẳng d1: \(\left\{{}\begin{matrix}x=t\\y=2-t\end{matrix}\right.\)(t∈R) và d2: x - 2y + m = 0 đến gốc toạ độ bằng 2

Những câu hỏi liên quan
a) Tìm tất cả các giá trị của tham số m đẻ khoảng cách từ giao điểm của hai đường thẳng d_1:left{{}begin{matrix}xty2-tend{matrix}right. và d_2:x-2y+m0 đến gốc tọa độ bằng 2 b) Trong mp xOy cho hai điểm A(2;3) B(1;4) . Đường thẳng cách đều hai điểm là c) Trong mp xOy cho hai điểm A(0;1) B(12;5) C(-3;0). Đường thẳng cách đều ba điểm là ...
Đọc tiếp
a) Tìm tất cả các giá trị của tham số m đẻ khoảng cách từ giao điểm của hai đường thẳng \(d_1:\left\{{}\begin{matrix}x=t\\y=2-t\end{matrix}\right.\) và \(d_2:x-2y+m=0\) đến gốc tọa độ bằng 2
b) Trong mp xOy cho hai điểm A(2;3) B(1;4) . Đường thẳng cách đều hai điểm là
c) Trong mp xOy cho hai điểm A(0;1) B(12;5) C(-3;0). Đường thẳng cách đều ba điểm là
Gọi giao điểm là A, thay tọa độ tham số d1 vào d2:
\(t-2\left(2-t\right)+m=0\Leftrightarrow3t+m-4=0\Rightarrow t=\dfrac{-m+4}{3}\)
\(\Rightarrow A\left(\dfrac{-m+4}{3};\dfrac{m+2}{3}\right)\)
\(\Rightarrow OA=\sqrt{\left(\dfrac{-m+4}{3}\right)^2+\left(\dfrac{m+2}{3}\right)^2}=2\)
\(\Leftrightarrow m^2-2m-8=0\Rightarrow\left[{}\begin{matrix}m=4\\m=-2\end{matrix}\right.\)
b. Bạn không đưa 4 đáp án thì không ai trả lời được câu hỏi này. Có vô số đường thẳng cách đều 2 điểm, chia làm 2 loại: các đường thẳng song song với AB và các đường thẳng đi qua trung điểm của AB
c. Tương tự câu b, do 3 điểm ABC thẳng hàng nên có vô số đường thẳng thỏa mãn, là các đường thẳng song song với AB
Đúng 2
Bình luận (1)
Tìm tất cả giá trị của tham số m để khoảng cách từ giao điểm của hai đường thẳng d1: \(\left\{{}\begin{matrix}x=t\\y=2-t\end{matrix}\right.\)(t∈R) và d2: x - 2y + m = 0 đến góc toạ độ bằng 2
trong mặt phẳng hệ toạ độ Oxy cho đường thẳng \(d:\left\{{}\begin{matrix}2+t\\1-3t\end{matrix}\right.\) và hai điểm A(1;2), B(-2;m). Tìm tất cả các giá trị tham số m để A và B nằm cùng phía đối với d.
\(\left\{{}\begin{matrix}x=2+t\\y=1-3t\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3x=6+3t\\y=1-3t\end{matrix}\right.\) \(\Rightarrow3x+y=7\Rightarrow3x+y-7=0\)
Vậy (d) có pt tổng quát là: \(3x+y-7=0\)
A và B nằm cùng phía đối với d khi và chỉ khi:
\(\left(3.1+2-7\right)\left(3.\left(-2\right)+m-7\right)>0\)
\(\Leftrightarrow-2\left(m-13\right)>0\)
\(\Rightarrow m< 13\)
Đúng 1
Bình luận (0)
Cho 2 đường thẳng :
d1\(\left\{{}\begin{matrix}x=2-3t\\y=1-t\end{matrix}\right.\)
d2\(\left\{{}\begin{matrix}x=-1-2t\\y=3-t\end{matrix}\right.\)
a, Tìm tọa độ điểm M của d1 và d2
b, Viết phương trình tham số và phương trình tổng quát của đường thẳng đi qua M và vuông góc với d1 d2
a. Md1= (2;1)
Md2 = (-1;3)
b. Gọi d là đường thẳng đi qua M
- Viết PTTS của d ⊥ d1:
Ta có:
M(2;1)
Do d1⊥ d nên VTCP ud1 = (-3;-1) --> VTPT nd = (-1;3)
--> VTCP ud = (3;1)
Vậy PTTS của d:
\(\left\{{}\begin{matrix}x=2+3t\\y=1+t\end{matrix}\right.\)
- Viết PTTQ của d ⊥ d1:
Ta có:
M(2;1)
Do d1 ⊥ d nên VTCP ud1 = (-3;-1) --> VTPT nd = (-1;3)
Vậy PTTQ của d:
-1(x - 2) + 3(y - 1) = 0
<=> -x + 2 + 3y - 3 = 0
<=> -x + 3y - 1 = 0
- Viết PTTS của d ⊥ d2:
Ta có:
M(-1;3)
Do d ⊥ d2 nên VTCP ud2 = (-2;-1) --> VTPT ud = (-1;2)
--> VTCP ud = (2;1)
Vậy PTTS của d:
\(\left\{{}\begin{matrix}x=-1+2t\\y=3+t\end{matrix}\right.\)
Viết PTTQ của d ⊥ d2:
M(-1;3)
Do d ⊥ d2 nên VTCP ud2 = (-2;-1) --> VTPT ud = (-1;2)
Vậy PTTQ của d:
-1(x + 1) + 2(y - 3) = 0
<=> -x - 1 + 2y - 6 = 0
<=> -x + 2y - 7 = 0
Đúng 0
Bình luận (0)
cho đường thẳng △ có phương trình tham số: \(\left\{{}\begin{matrix}x=1+2t\\y=-3-t\end{matrix}\right.\)
a) viết phương trình tổng quát của đg thẳng △
b) cho đg thẳng d1: x+2y-8=0 và d2: x-2y=0. viết phương trình tổng quát của đg thẳng đi qua giao điểm của d1 với d2 và vuông góc với △
giúp mk vs ạ mk cần gấp
a: Δ có vtcp là (2;-1) và đi qua A(1;-3)
=>VTPT là (1;2)
PTTQ là:
1(x-1)+2(y+3)=0
=>x-1+2y+6=0
=>x+2y+5=0
b: Vì d vuông góc Δ nên d: 2x-y+c=0
Tọa độ giao của d1 và d2 là:
x+2y=8 và x-2y=0
=>x=4 và y=2
Thay x=4 và y=2 vào 2x-y+c=0, ta được
c+2*4-2=0
=>c=-2
Đúng 0
Bình luận (0)
Phương trình tham số của đường thẳng d đi qua hai điểm M(2; -1) và N(1; 0) làA. left{{}begin{matrix}text{x}2+ty-1+tend{matrix}right.left(tintext{R}right) B. left{{}begin{matrix}text{x}2-ty-1+tend{matrix}right.left(tin Rright)C. left{{}begin{matrix}text{x}2+2ttext{y}-1+tend{matrix}right.left(tin Rright) D. left{{}begin{matrix}text{x}2+ty-1+2tend{matrix}right.left(tin Rright)
Đọc tiếp
Phương trình tham số của đường thẳng d đi qua hai điểm M(2; -1) và N(1; 0) là
A. \(\left\{{}\begin{matrix}\text{x}=2+t\\y=-1+t\end{matrix}\right.\left(t\in\text{R}\right)\) B. \(\left\{{}\begin{matrix}\text{x}=2-t\\y=-1+t\end{matrix}\right.\left(t\in R\right)\)
C. \(\left\{{}\begin{matrix}\text{x}=2+2t\\\text{y}=-1+t\end{matrix}\right.\left(t\in R\right)\) D. \(\left\{{}\begin{matrix}\text{x}=2+t\\y=-1+2t\end{matrix}\right.\left(t\in R\right)\)
Với giá trị nào của tham số m thì hai đường thẳng\(d_1:\left\{{}\begin{matrix}x=m+1-6t\\y=3t\end{matrix}\right.\) và \(d_2:\left\{{}\begin{matrix}x=-2-2m^2t\\2+\left(2m^2+m-2\right)t\end{matrix}\right.\) trùng nhau?
Lời giải:
Viết lại đt $(d_1)$:
$x+2y=m+1-6t+6t$
$\Leftrightarrow x+2y=m+1$
Ta thấy $M(-2,2)\in (d_2)$. Nếu $(d_2)\equiv (d_1)$ thì:
$M(-2,2)\in (d_1)$
$\Leftrightarrow -2+2.2=m+1$
$\Leftrightarrow m=1$
Thay giá trị $m$ vừa tìm được vào 2 ptđt ban đầu thì:
$(d_1)$: $x+2y=2$
$(d_2)$: \(\left\{\begin{matrix} x=-2-2t\\ y=2+t\end{matrix}\right.\)
$\Rightarrow x+2y=-2-2t+2(2+t)=2$ (trùng với $(d_1)$)
Vậy $m=1$
Đúng 1
Bình luận (0)
bài 1: ko giải hệ phương trình, dự đoán số nghiệm của các hệ phương trình sau:
a) left{{}begin{matrix}3x+2y40x+4y-8end{matrix}right. b)left{{}begin{matrix}0x-5y-112x-0y2sqrt{3}end{matrix}right.
c)left{{}begin{matrix}-2x+ydfrac{1}{2}-3x+dfrac{3}{2}ydfrac{3}{4}end{matrix}right. d) left{{}begin{matrix}2sqrt{2}x+4y3-sqrt{2}x-2ydfrac{3}{2}end{matrix}right.
bài 2: cho hệ phương trình left{{}begin{matrix}x+y1mx+y2mend{matrix}right. xác định các giá trị của t...
Đọc tiếp
bài 1: ko giải hệ phương trình, dự đoán số nghiệm của các hệ phương trình sau:
a) \(\left\{{}\begin{matrix}3x+2y=4\\0x+4y=-8\end{matrix}\right.\) b)\(\left\{{}\begin{matrix}0x-5y=-11\\2x-0y=2\sqrt{3}\end{matrix}\right.\)
c)\(\left\{{}\begin{matrix}-2x+y=\dfrac{1}{2}\\-3x+\dfrac{3}{2}y=\dfrac{3}{4}\end{matrix}\right.\) d) \(\left\{{}\begin{matrix}2\sqrt{2}x+4y=3\\-\sqrt{2}x-2y=\dfrac{3}{2}\end{matrix}\right.\)
bài 2: cho hệ phương trình \(\left\{{}\begin{matrix}x+y=1\\mx+y=2m\end{matrix}\right.\) xác định các giá trị của tham số m để hệ phương trình:
a) có nghiệm duy nhất b) vô nghiệm
c) vô số nghiệm
bài 3: hãy kiểm tra xem mỗi cặp số sau có là nghiệm của hệ phương trình tương ứng hay ko ?
a) (1;2) và \(\left\{{}\begin{matrix}3x-5y=-7\\2x+y=4\end{matrix}\right.\) b) (-2;5) và \(\left\{{}\begin{matrix}2x-3y=-19\\-3x+2y=7\end{matrix}\right.\)
bài 4: cho hệ phương trình \(\left\{{}\begin{matrix}2mx+y=m\\x-my=-1-6m\end{matrix}\right.\) Tìm các giá trị của tham số m để cặp số ( -2;1) là nghiệm của hệ phương đã cho.
bài 5: cho 2 phương trình đường thẳng:
d1: 2x-y=5 và d2: x-2y=1
a) vẽ hai đường thẳng d1 và d2 trên cùng một hệ trục tọa độ.
b) từ đò thị của d1 và d2 tìm nghiệm của hệ phương trình:
\(\left\{{}\begin{matrix}2x-y=5\\x-2y=1\end{matrix}\right.\)
c) cho đường thẳng d3: mx+(2m-1)y=3. Tìm các giá trị của tham số m để ba đường thẳng d1, d2 và d3 đồng quy.
cảm ơn mn nhé !
Bài 5:
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}2x-y=5\\2x-4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1\\x=1+2y=3\end{matrix}\right.\)
c; THay x=3 và y=1 vào (d3), ta được:
3m+1(2m-1)=3
=>5m-1=3
=>5m=4
=>m=4/5
Đúng 0
Bình luận (0)
1.Cho pt 2x+3y300.Pt có bao nhiêu nghiệm nguyên dương?
2.Cho hệ pt left{{}begin{matrix}ax+y3left(1right)x-2y2left(2right)end{matrix}right..Gọi D1,D2 lần lượt là các đường thẳng có pt (1) và (2).Tìm a biết rằng có điểm A trên D1 và điểm B trên D2 t/m left{{}begin{matrix}x_Ax_Bne0y_A+3y_B0end{matrix}right.
3.Cho hệ pt left{{}begin{matrix}left(m+1right)x+8y4mmx+left(m+3right)y3m-1end{matrix}right..Tìm giá trị nguyên của m để hệ có nghiệm duy nhất (x;y) vs x,y có giá trị nguyên
Đọc tiếp
1.Cho pt 2x+3y=300.Pt có bao nhiêu nghiệm nguyên dương?
2.Cho hệ pt \(\left\{{}\begin{matrix}ax+y=3\left(1\right)\\x-2y=2\left(2\right)\end{matrix}\right.\).Gọi D1,D2 lần lượt là các đường thẳng có pt (1) và (2).Tìm a biết rằng có điểm A trên D1 và điểm B trên D2 t/m \(\left\{{}\begin{matrix}x_A=x_B\ne0\\y_A+3y_B=0\end{matrix}\right.\)
3.Cho hệ pt \(\left\{{}\begin{matrix}\left(m+1\right)x+8y=4m\\mx+\left(m+3\right)y=3m-1\end{matrix}\right.\).Tìm giá trị nguyên của m để hệ có nghiệm duy nhất (x;y) vs x,y có giá trị nguyên
1)
2x + 3y = 300
Ta thấy 3y \(⋮\) 3 ; 300 \(⋮\) 3
=> 2x \(⋮\) 3
=> x \(⋮\) 3
đặt x = 3n ( n >0)
=> 2x + 3y = 300
=> 6n + 3y = 300
=> y = \(\dfrac{\left(300-6n\right)}{3}=\left(100-2n\right)\)
Vì y là số nguyên dương => y > 0
=> 100 - 2n > 0
=> 50 > n
=> 0<n<50
=> số nghiệm nguyên dương thoả mãn phương trình là :
(49-1):1+1 = 49 (nghiệm).
Đúng 0
Bình luận (0)