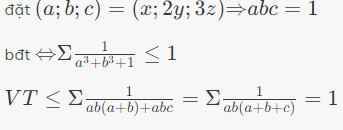Ta có \(\left(\frac{1}{2}x+y\right)\left(...\right)=\frac{x^3+8y^3}{8}\)

\(\Leftrightarrow8\left(\frac{1}{2}x+y\right)\left(...\right)=x^3-8y^3\)

\(\Leftrightarrow4\left(x+2y\right)\left(...\right)=\left(x+2y\right)\left(x^2-2xy+4y^2\right)\)

\(\Rightarrow4\left(...\right)=x^2-2xy+4y^2\)

\(\Rightarrow\left(...\right)=\frac{x^2-2xy+4y^2}{4}\)

Vậy đccm

#Học tốt

Ta có VP = \(\frac{x^3+8y^3}{8}\)

VP=\(\frac{x^3}{8}+y^3\)=\(\left(\frac{x}{2}\right)^3+y^3\)=\(\left(\frac{x}{2}+y\right)\).\(\left(\frac{x^2}{4}-\frac{xy}{2}+y^2\right)\)

Vậy \(\left(\frac{x^2}{4}-\frac{xy}{2}+y^2\right)\)

a/ĐKXĐ: \(y\ne4\)

Đặt \(y-4=x\)

\(1+\frac{45}{x^2}=\frac{14}{x}\Leftrightarrow x^2-14x+45=0\Rightarrow\left[{}\begin{matrix}x=9\\x=5\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}y-4=9\\y-4=5\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}y=13\\y=9\end{matrix}\right.\)

b/ ĐKXĐ: \(x\ne1\)

Đặt \(x-1=y\)

\(\frac{5}{y}-\frac{4}{3y^2}=3\Leftrightarrow9y^2=15y-4\)

\(\Leftrightarrow9y^2-15y+4=0\Rightarrow\left[{}\begin{matrix}y=\frac{4}{3}\\y=\frac{1}{3}\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x-1=\frac{4}{3}\\x-1=\frac{1}{3}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\frac{7}{3}\\x=\frac{4}{3}\end{matrix}\right.\)

c/ ĐKXĐ: \(x\ne5\)

\(\Leftrightarrow2x-5=3x-15\)

\(\Leftrightarrow x=10\)

d/ ĐKXĐ: \(x\ne0\)

\(\Leftrightarrow2\left(x^2-12\right)=2x^2+3x\)

\(\Leftrightarrow3x=-24\Rightarrow x=-8\)

e/ ĐKXĐ: \(x\ne2\)

\(\Leftrightarrow\left(x-2\right)\left(x+2\right)-3\left(x-2\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(x-1\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x=2\left(l\right)\\x=1\end{matrix}\right.\)

f/ DKXĐ: \(x\ne-\frac{1}{2}\)

\(\Leftrightarrow\left(2x-1\right)\left(2x+1\right)=8\)

\(\Leftrightarrow4x^2-1=8\)

\(\Leftrightarrow x^2=\frac{9}{4}\Rightarrow x=\pm\frac{3}{2}\)

\(2,\left\{{}\begin{matrix}x^3-2x^2y-15x=6y\left(2x-5-4y\right)\left(1\right)\\\frac{x^2}{8y}+\frac{2x}{3}=\sqrt{\frac{x^3}{3y}+\frac{x^2}{4}}-\frac{y}{2}\left(2\right)\end{matrix}\right.\)

\(\left(1\right)\Leftrightarrow\left(2y-x\right)\left(x^2-12y-15\right)=0\)\(\Leftrightarrow\left[{}\begin{matrix}2y=x\\y=\frac{x^2-15}{12}\end{matrix}\right.\)

Ta xét các trường hợp sau:

Trường hợp 1:

\(y=\frac{x^2-15}{12}\) thay vào phương trình \(\left(2\right)\) ta được:

\(\frac{3x^2}{2\left(x^2-15\right)}+\frac{2x}{3}=\sqrt{\frac{4x^3}{x^2-15}+\frac{x^2}{4}}-\frac{x^2-15}{24}\)

\(\Leftrightarrow\frac{36x^2}{x^2-15}-12\sqrt{\frac{x^2}{x^2-15}\left(x^2+16x-15\right)}+\left(x^2+16x-15\right)=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}x^2+16x-15\ge0\\6\sqrt{\frac{x^2}{x^2-15}}=\sqrt{\left(x^2+16x-15\right)}\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x^2+16x-15\ge0\\36\frac{x^2}{x^2-15}=x^2+16x-15\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x^2+16x-15\ge0\\36x^2=\left(x^2-15\right)\left(x^2+16x-15\right)\left(3\right)\end{matrix}\right.\)

Ta xét phương trình \(\left(3\right):36x^2=\left(x^2-15\right)\left(x^2+16x-15\right)\)

Vì: \(x=0\) Không phải là nghiệm. Ta chia cả hai vế p.trình cho \(x^2\) ta được:

\(36=\left(x-\frac{15}{x}\right)\left(x+16-\frac{15}{x}\right)\)

Đặt: \(x-\frac{15}{x}=t\Rightarrow t^2+16t-36=0\Leftrightarrow\left[{}\begin{matrix}t=2\\t=-18\end{matrix}\right.\)

+ Nếu như:

\(t=2\Leftrightarrow x-\frac{15}{x}=2\Leftrightarrow x^2-2x-15=0\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-3\end{matrix}\right.\)\(\Leftrightarrow x=5\)

+ Nếu như:

\(t=-18\Leftrightarrow x-\frac{15}{x}=-18\Leftrightarrow x^2+18x-15=0\Leftrightarrow\left[{}\begin{matrix}x=-9-4\sqrt{6}\\x=-9+4\sqrt{6}\end{matrix}\right.\Leftrightarrow x=-9-4\sqrt{6}\)

Trường hợp 2:

\(x=2y\) thay vào p.trình \(\left(2\right)\) ta được:

\(\Leftrightarrow\frac{x^2}{4x}+\frac{2x}{3}=\sqrt{\frac{2x^3}{3x}+\frac{x^2}{4}}-\frac{x}{4}\Leftrightarrow\frac{7}{6}x=\sqrt{\frac{11x^2}{12}}\Leftrightarrow x=0\left(ktmđk\right)\)

Vậy nghiệm của hệ đã cho là: \(\left(x,y\right)=\left(5;\frac{5}{6}\right),\left(-9-4\sqrt{6};\frac{27+12\sqrt{6}}{2}\right)\)

Năm mới chắc bị lag @@ tớ sửa luôn đề câu 3 nhé :v

3, \(\left\{{}\begin{matrix}8\left(x^2+y^2\right)+4xy+\frac{5}{\left(x+y\right)^2}=13\left(1\right)\\2xy+\frac{1}{x+y}=1\left(2\right)\end{matrix}\right.\)

\(\left(1\right)\Leftrightarrow8\left[\left(x+y\right)^2-2xy\right]+4xy+\frac{5}{\left(x+y\right)^2}=13\)

Đặt \(\left\{{}\begin{matrix}x+y=a\\xy=b\end{matrix}\right.\)

\(\left(1\right)\Leftrightarrow8\left(a^2-2b\right)+4b+\frac{5}{a^2}=13\)

\(\Leftrightarrow8a^2-12b+\frac{5}{a^2}=13\)

Ta cũng có \(\left(2\right)\Leftrightarrow2b+\frac{1}{a}=1\)

\(\Leftrightarrow2b=1-\frac{1}{a}\)

Thay vào (1) ta được :

\(8a^2+\frac{5}{a^2}-6\cdot\left(1-\frac{1}{a}\right)=13\)

\(\Leftrightarrow8a^2+\frac{5}{a^2}-6+\frac{6}{a}=13\)

\(\Leftrightarrow8a^2+\frac{5}{a^2}+\frac{6}{a}=19\)

Giải pt được \(a=1\)

Khi đó \(b=\frac{1-\frac{1}{1}}{2}=0\)

Ta có hệ :

\(\left\{{}\begin{matrix}x+y=1\\xy=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=0\\y=1\end{matrix}\right.\\\left\{{}\begin{matrix}x=1\\y=0\end{matrix}\right.\end{matrix}\right.\)

Vậy...

Cần cù thì bù thông minh

Chỉ có lm thì ms có ăn

Ko lm mà mún đòi ăn

Thì có ăn ***** ăn đầu bird

Trích chú của mày

Bài 1: \(T=\sqrt{\frac{x^3}{x^3+8y^3}}+\sqrt{\frac{4y^3}{y^3+\left(x+y\right)^3}}\)

\(=\frac{x^2}{\sqrt{x\left(x^3+8y^3\right)}}+\frac{2y^2}{\sqrt{y\left[y^3+\left(x+y\right)^3\right]}}\)

\(=\frac{x^2}{\sqrt{\left(x^2+2xy\right)\left(x^2-2xy+4y^2\right)}}+\frac{2y^2}{\sqrt{\left(xy+2y^2\right)\left(x^2+xy+y^2\right)}}\)

\(\ge\frac{2x^2}{2x^2+4y^2}+\frac{4y^2}{2y^2+\left(x+y\right)^2}\ge\frac{2x^2}{2x^2+4y^2}+\frac{4y^2}{2x^2+4y^2}=1\)

\(\Rightarrow T\ge1\)

Bài 2:

[Toán 10] Bất đẳng thức | Page 5 | HOCMAI Forum - Cộng đồng học sinh Việt Nam

đặt \(\left(a;b;c\right)=\left(x;2y;3z\right)\)\(\Rightarrow\)\(abc=1\)

bđt \(\Leftrightarrow\)\(\Sigma\frac{1}{a^3+b^3+1}\le1\)

\(VT\le\Sigma\frac{1}{ab\left(a+b\right)+abc}=\Sigma\frac{1}{ab\left(a+b+c\right)}=1\)