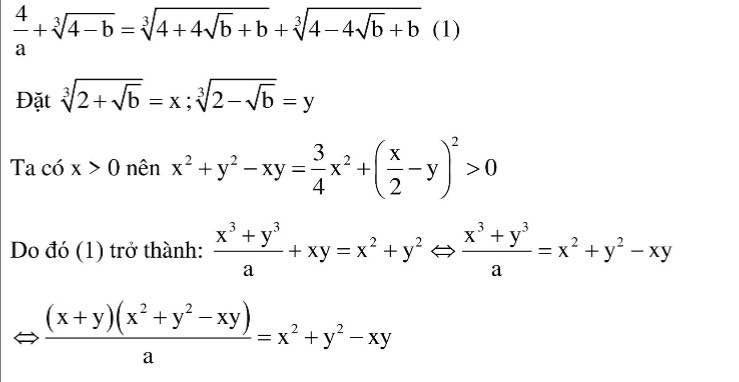tìm nghiệm nguyên dương: \(\sqrt{a}+\sqrt{b}=\sqrt{2012}\)

Những câu hỏi liên quan
Tìm nghiệm nguyên dương của phương trình sau:
\(\sqrt{x}+\sqrt{y}=\sqrt{2012}\)
và \(\sqrt{x}=\sqrt{2012}=2\sqrt{503}-\sqrt{y}\)
=> \(x=2012-4\sqrt{503y}+y\) là số nguyên dương
=> \(\sqrt{503y}\) là số nguyên dương
mà 503 là số nguyên tố và 0 < y < 2012
=> y = 503
=> x = 503
Kết luận:...
Bài đc đăng vào ngày 14/8/2019 mà đến 19/6/2020 mới đc giải?
tìm nghiệm nguyên dương của pt: \(\sqrt{x} +\sqrt{y}=\sqrt{2012}\)
từ đề bài => 0 < x; y < 2012 và
\(\sqrt{y}=\sqrt{2012}-\sqrt{x}\Rightarrow y=\left(\sqrt{2012}-\sqrt{x}\right)^2=2012+x-2\sqrt{2012}\sqrt{x}=2012+x-4.\sqrt{503.x}\)Vì y nguyên nên \(\sqrt{503.x}\) nguyên => x = 503.k2 Mà 0< x < 2012 =>0< 503. k2 < 2012 => 0< k2 < 4 => k2 = 1
=> x = 503 => y = 2012 + 503 - 4.503 = 503
Vậy x = y = 503
Đúng 0
Bình luận (0)
1. Tìm các số nguyên dương a; b sao cho:dfrac{4}{a} + 3sqrt{4-b} 3sqrt{4+4sqrt{b}+b} + 3sqrt{4-4sqrt{b}+b}2. Giải phương trình nghiệm nguyênx^3-y^3-6x^2+12x27
Đọc tiếp
1. Tìm các số nguyên dương a; b sao cho:
\(\dfrac{4}{a}\) \(+\) 3\(\sqrt{4-b}\) \(=\) 3\(\sqrt{4+4\sqrt{b}+b}\) \(+\) 3\(\sqrt{4-4\sqrt{b}+b}\)
2. Giải phương trình nghiệm nguyên
\(x^3-y^3-6x^2+12x=27\)
đăng câu hỏi kiểu j mà đặng đc lên như thế này đấy
Đúng 0
Bình luận (0)
1.
Đặt \(\sqrt[3]{2+\sqrt{b}}=x;\sqrt[3]{2-\sqrt{b}}=y\)
Do \(x>0\Rightarrow x^2+y^2-xy=\dfrac{3}{4}x^2+\left(\dfrac{1}{2}x-y\right)^2>0\)
\(PT\Leftrightarrow\dfrac{x^3+y^3}{a}+xy=x^2+y^2\Leftrightarrow\dfrac{\left(x+y\right)\left(x^2-xy+y^2\right)}{a}=x^2-xy+y^2\\ \Leftrightarrow\left(x^2-xy+y^2\right)\left(\dfrac{x+y}{a}-1\right)=0\\ \Leftrightarrow\dfrac{x+y}{a}=1\\ \Leftrightarrow\sqrt[3]{2+\sqrt{b}}+\sqrt[3]{2-\sqrt{b}}=a\left(1\right)\\ \Leftrightarrow\left(\sqrt[3]{2+\sqrt{b}}+\sqrt[3]{2-\sqrt{b}}\right)^3=a^3\\ \Leftrightarrow4+3a\sqrt[3]{4-b}=a^3\left(2\right)\\ \Rightarrow4-b=\left(\dfrac{a^3-4}{3a}\right)^3\)
Mặt khác \(b\in \mathbb{Z^+}\)
\(\Rightarrow\left(a^3-4\right)⋮3a\Rightarrow\left(a^3-4\right)⋮a\\ \Rightarrow4⋮a\Rightarrow a\in\left\{1;2;4\right\}\)
Với \(a=1\Rightarrow4-b=1\Rightarrow b=5\)
Với \(a=2;a=4\Rightarrow b\notin \mathbb{Z}\)
Vậy \(\left(a;b\right)=\left(1;5\right)\)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
Tìm nghiệm nguyên dương của phương trình : \(\sqrt{x+2\sqrt{3}}=\sqrt{y}+\sqrt{z}\)
\(\Rightarrow x+2\sqrt{3}=y+z+2\sqrt{yz}\)
\(\Rightarrow2\sqrt{yz}=\left(x-y-z\right)+2\sqrt{3}\)
\(\Rightarrow4yz=\left(x-y-z\right)^2+12+4\sqrt{3}\left(x-y-z\right)\)
\(\Rightarrow4\sqrt{3}\left(x-y-z\right)=4yz-12-\left(x-y-z\right)^2\) (1)
\(\sqrt{3}\) là số vô tỉ nên đẳng thức xảy ra khi: \(x-y-z=0\)
Thay ngược vào (1) \(\Rightarrow yz=3\Rightarrow\left(y;z\right)=\left(1;3\right);\left(3;1\right)\)
\(\Rightarrow\sqrt{x+2\sqrt{3}}=\sqrt{4+2\sqrt{3}}\Rightarrow x=4\)
Đúng 0
Bình luận (0)
Tìm nghiệm nguyên dương của phương trình \(\sqrt{x+y+3}+1=\sqrt{x}+\sqrt{y}\).
\(\sqrt{x+y+3}+1=\sqrt{x}+\sqrt{y}\)
Bình phương 2 vế, ta có:
\(x+y+3+1=x+y\)
\(x+y+3+1-x-y=0\)
\(4=0\) (vô lý)
Vậy phương trình vô nghiệm
-Chúc bạn học tốt-
Đúng 0
Bình luận (3)
(x,y) hoán vị của (4,9) . có vẻ hoạt động
Đúng 0
Bình luận (0)
Tìm nghiệm nguyên dương: \(\sqrt{x+3\sqrt{3}}=\sqrt{y}+\sqrt{z}\)
\(\sqrt{x+3\sqrt{3}}=\sqrt{y}+\sqrt{z}\)
\(\Leftrightarrow3\sqrt{3}-2\sqrt{yz}=y+z-x\)
Ta có VP là số nguyên nên VT cũng phải là số nguyên
Giả sử \(yz=a^2\) thì VT không phải số nguyên
Nên yz không phải số chính phương.
Nên để VT là số nguyên thì chỉ có thể là O
\(\Rightarrow3\sqrt{3}=2\sqrt{yz}\)
\(\Rightarrow yz=\frac{27}{4}\) loại vì yz là số nguyên dương
Vậy PT vô nghiệm
Đúng 0
Bình luận (0)
tìm nghiệm nguyên dương của phuong trinh $\sqrt{x}+\sqrt{y}=\sqrt{x+y}+2$
Tìm x,y nguyên dương để: \(\sqrt{x-1}+\sqrt{y+1}=\sqrt{\frac{\left(x-1\right)\left(y+1\right)}{2012}}\)
Mong các bạn ủng hộ cho kênh youtube của mình nha !!
Tên youtube:P Music
Link:https://www.youtube.com/channel/UCs0JKZKs4zoDYqqtAmtiBBA?view_as=subscriber
Nhóm của mình gồm có:
Hậu Trần YTVN
Vanh_GoG_VN
M.Ichibi
P Music(là mình)
Mong các bạn ủng hộ nha !!
Tìm x,y nguyên dương : biết \(\sqrt{x}+\sqrt{y}=2012\)