cho tam giác ABC có AB=7cm BC=11cm AC=13cm.
a) Tính diện tích tam giác
b) tính R, r
Cho tam giác ABC có BC = a, AC = b, AB = c và (I;r) là đường tròn nội tiếp tam giác (Hình 11).
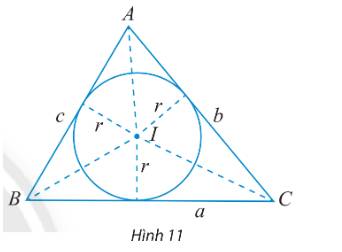
a) Tính diện tích các tam giác IBC, IAC, IAB theo r và a, b, c.
b) Dùng kết quả trên để chứng minh công thức tính diện tích tam giác ABC: \(S = \frac{{r(a + b + c)}}{2}\)
a) Diện tích \({S_1}\) của tam giác IAB là: \({S_1} = \frac{1}{2}r.AB = \frac{1}{2}r.c\)
Diện tích \({S_2}\) của tam giác IAC là: \({S_2} = \frac{1}{2}r.AC = \frac{1}{2}r.b\)
Diện tích \({S_3}\) của tam giác IBC là: \({S_3} = \frac{1}{2}r.BC = \frac{1}{2}r.a\)
b) Diện tích S của tam giác ABC là:
\(\begin{array}{l}S = {S_1} + {S_2} + {S_3} = \frac{1}{2}r.c + \frac{1}{2}r.b + \frac{1}{2}r.a = \frac{1}{2}r.(c + b + a)\\ \Leftrightarrow S = \frac{{r(a + b + c)}}{2}\end{array}\)
Cho tam giác ABC vuông tại a a tính AC biết BC=13cm AB=5cm b tính BC biết AB=4cm AC=7cm
a, Áp dụng định lý Pitago:
`AB^2 + AC^2 = BC^2`
`=> 25 + AC^2 = 169`
`=> AC^2 = 144`
`=> sqrt 144 = 12`.
b. Áp dụng định lý Pytago ta có:
`AB^2 + AC^2 = BC^2`
`16 + 49 = BC^2`
`BC^2 = 65`
`BC = sqrt 65`.
Áp dụng định lí Pitago trong tam giác ABC vuông tại A
AC = BC2 + AB2
= 132 + 52
= \(\sqrt{194}\) = 14 cm
Áp dụng định lí Pitago trong tam giác ABC cân tại A
BC = AB2 + AC2
= 42 + 72
= \(\sqrt{65}\) = 8 cm
Cho tam giác ABC có AB=13cm, AC=20cm. Trên BC lấy điểm D sao cho CD=11cm và AD=13cm. Tính BC
Cho tam giác ABC có góc A bằng 60 độ , AB=2cm, AC= 4cm.
a) Tím diện tích tam giác ABC
b) Tính BC
c) Gọi r là bán kính đường tròn nội tiếp tam giác ABC . Tính r
Cho tam giác ABC có góc B bằng 60 độ, AC=13cm, BC-BA=7cm. Tính AB,BC?
p dụng định lí hàm số cos của tam giác thường ta có:
AC² = AB² + BC² - 2AB.AC.c0s60*
13² = AB² + BC² - AB.BC (1)
giả thiết: BC - AB = 7 --> BC = 7 + AB thay vào (1)
1<=> 169 = AB² + (7 + AB²) - AB(7 + AB)
<=> 169 = AB² + 49 + 14AB + AB² - 7AB - AB²
<=> AB² + 7AB - 120 = 0
<=> AB = 8 --> BC = 15
.......AB = -15 ( LOẠI, cạnh không âm)
Bài 1:
Cho tam giác ABC, góc A=90 độ
a) AB=12cm, AC=15cm. Tính BC
b) AB=7cm, BC=11cm. Tính AC
Bài 2:
Tam giác có độ dài ba cạnh như sau có là tam giác vuông không
a) 17cm, 8cm, 15cm
b) 5dm, 7dm, 9dm
Bài 2:
a: Đây là tam giác vuông
b: Đây ko là tam giác vuông
Cho tam giác ABC vuông tại A có AB = 5cm, BC = 13cm. AH là đường cao.
a) Tính BH, CH, AC và AH.
b) Tính các góc B và C của tam giác ABC.
c) Gọi M là trung điểm của BC tính diện tích tam giác AHM
\(a,AC=\sqrt{BC^2-AB^2}=12\left(cm\right)\left(pytago\right)\)
Áp dụng HTL:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH^2=BH\cdot HC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=\dfrac{25}{13}\left(cm\right)\\CH=\dfrac{AC^2}{BC}=\dfrac{144}{13}\left(cm\right)\\AH=\sqrt{\dfrac{25}{13}\cdot\dfrac{144}{13}}=\dfrac{60}{13}\left(cm\right)\end{matrix}\right.\)
\(b,\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{12}{13}\approx\sin67^0\Leftrightarrow\widehat{B}\approx67^0\\ \Rightarrow\widehat{C}=90^0-\widehat{B}=23^0\)
\(c,\) Vì AM là trung tuyến ứng ch BC nên \(AM=BM=\dfrac{1}{2}BC=\dfrac{13}{2}\left(cm\right)\)
Ta có \(MH=MB-HB=6,5-\dfrac{25}{13}=\dfrac{119}{26}\left(cm\right)\)
Vậy \(S_{AMH}=\dfrac{1}{2}AH\cdot HM=\dfrac{1}{2}\cdot\dfrac{60}{13}\cdot\dfrac{119}{26}=\dfrac{1785}{169}\left(cm^2\right)\)
Cho tam giác ABC có AB=4cm, BC=7cm, AC=9cm. Tính cosA và diện tích tam giác
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2AB.AC}=\dfrac{2}{3}\)
\(sinA=\sqrt{1-cos^2A}=\dfrac{\sqrt{5}}{3}\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}AB.AC.sinA=6\sqrt{5}\)
Cho tam giác ABC có AM là trung tuyến, Trên tia đối của tia AM lấy điểm E sao cho MÀ=ME
a) Chứng minh tứ giác ABRC là hình bình hành
b)tìm điều kiện của tam giác ABC để tứ giác ABEC là hình vuông.
C) nếu tam giác ABC vuông tại A và BC=13cm. AC vad AB hơn kém nhau 7cm. Tính diện tích tứ giác ABEC