cho đa thức f(x)=(x+1)(x2-2)2012
a) tính f(1);f(-1)
b) gọi M và N lần lượt là tổng các hệ số của các hạng tử bậc chẵn của đa thức f(x) sau khi đã khai triển và rút gọn. Tính M và N
Cho đa thức f(x) thỏa mãn f(x)+3.f(1/x)=x2. Tính f(2)
Bài 1: Cho đa thức f(x) = 2x – x2 + 2|x + 1|.
a) Thu gọn đa thức f(x).
b) Tính giá trị của f(x) khi x = –3/2.
Ví dụ 1 (30s): Cho đa thức f(x) = (2x + 1)(x
2 − x + 1). Kết quả của phép chia đa thức f(x)
cho đa thức 2x + 1 là:
A. x
2 + x + 1 B. x
2 − x C. x
2 − x + 1 D. x
2 + 1
\(\dfrac{f\left(x\right)}{2x+1}=\dfrac{\left(2x+1\right)\left(x^2-x+1\right)}{2x+1}=x^2-x+1\)
Chọn C:
\(\dfrac{\left(2x+1\right)\left(x^2-x+1\right)}{2x+1}=x^2-x+1\)
Cho các đa thức f(x) = x5 – 3x2 + x3 – x2 - 2x + 5
g(x) = x5 – x4 + x2 - 3x + x2 + 1
a) Thu gọn và sắp xếp đa thức f(x) và g(x) theo luỹ thừa giảm dần.
b)Tính h(x) = f(x) + g(x)
a: \(F\left(x\right)=x^5-3x^2+x^3-x^2-2x+5\)
\(=x^5+x^3-4x^2-2x+5\)
\(G\left(x\right)=x^5-x^4+x^2-3x+x^2+1\)
\(=x^5-x^4+2x^2-3x+1\)
b: Ta có: \(H\left(x\right)=F\left(x\right)+G\left(x\right)\)
\(=x^5+x^3-4x^2-2x+5+x^5-x^4+2x^2-3x+1\)
\(=2x^5-x^4+x^3-2x^2-5x+6\)
Cho g(x) là 1 đa thức với hệ số nguyên. CM: Đa thức f(x)=x2+x.g(x3)f(x)=x2+x.g(x3) không chia hết cho đa thức: x2−x+1
1. Tính giá trị của đa thức F(x) = 2x2 – 3x – 2 tại x = -1; x = 0 ; x = 1; x = 2. Từ đó hãy tìm một nghiệm của đa thức F(x)
2. Tìm nghiệm của đa thức E(x) = x2 + x.
1. F(-1) = 2.(-1)2 – 3. (-1) – 2 = 2.1 + 3 – 2 = 3
F(0) = 2. 02 – 3 . 0 – 2 = -2
F(1) = 2.12 – 3.1 – 2 = 2 – 3 – 2 = -3
F(2) = 2.22 – 3.2 – 2 = 8 – 6 – 2 = 0
Vì F(2) = 0 nên 0 là 1 nghiệm của đa thức F(x)
2. Vì đa thức E(x) có hệ số tự do bằng 0 nên có một nghiệm là x = 0.
cho đa thức f(x) xác định với mọi x thỏa mãn
x.f(x+2) =( x2
-9).f(x)
1) tính f(5)
2) chứngminh rằng f(x) có ít nhất 3 nghiệm
\(a,f\left(5\right)\Rightarrow x=3\\ 3f\left(5\right)=0f\left(3\right)\Rightarrow f\left(5\right)=0\\ b,x=0\Rightarrow0f\left(2\right)=-9f\left(0\right)\Rightarrow f\left(0\right)=0\)
=> x = 0 là nghiệm
\(x=-3\Rightarrow-3f\left(-1\right)=\left(9-9\right)f\left(-3\right)=0f\left(-3\right)\\ \Rightarrow f\left(-1\right)=0\)
=> x = -1 là nghiệm
Theo ý a) ta có \(x=5\)
\(\Rightarrow f\left(x\right)\) có 3 nghiệm \(=\left\{0;-1;5\right\}\)
Cho hai đa thức:
f(x) = x5 – 3x2 + 7x4 – 9x3 + x2 - 1/4 x
g(x) = 5x4 – x5 + x2 – 2x3 + 3x2 - 1/4
Tính f(x) + g(x) và f(x) – g(x)
* Ta có:
f(x) = x5 – 3x2 + 7x4 – 9x3 + x2 - 1/4 x
= x5 – (3x2 – x2) + 7x4 – 9x3 -1/4.x
= x5 – 2x2 + 7x4 – 9x3 -1/4.x
= x5 + 7x4 – 9x3 – 2x2 - 1/4
g(x) = 5x4 – x5 + x2 – 2x3 + 3x2 - 1/4
= 5x4 –x5+ (x2 + 3x2) – 2x3 – 1/4
= 5x4 – x5 + 4x2 – 2x3 – 1/4
= -x5 + 5x4 – 2x3 + 4x2 - 1/4
* f(x) + g(x)
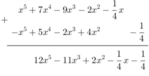
* f(x) - g(x)
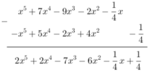
Cho hai đa thức f ( x ) = - x 2 - 2 x - 1 , g ( x ) = x 2 + 3 x - 1 . Tìm nghiệm cúa đa thức f ( x ) + g ( x ) là:
A. x = -2
B. x = -1
C. x = 1
D. x = 2
Ta có: f(x) + g(x) = x - 2. Cho x - 2 = 0 ⇒ x = 2. Chọn D
Tìm dư của phép chia đa thức f(x) cho (x2 +1) (x-2) biết f(x) (chia x-2) dư 7 và f(x) : (x2 +1) dư 3x+5
Để tìm dư của phép chia đa thức f(x) cho (x^2 + 1)(x - 2), chúng ta cần sử dụng định lý dư của đa thức. Theo định lý dư của đa thức, nếu chia đa thức f(x) cho đa thức g(x) và được dư đa thức r(x), thì ta có: f(x) = q(x) * g(x) + r(x) Trong trường hợp này, chúng ta biết rằng f(x) chia cho x - 2 dư 7 và chia cho x^2 + 1 dư 3x + 5. Vì vậy, chúng ta có các phương trình sau: f(x) = q(x) * (x - 2) + 7 f(x) = p(x) * (x^2 + 1) + (3x + 5) Để tìm dư của phép chia f(x) cho (x^2 + 1)(x - 2), ta cần tìm giá trị của r(x). Để làm điều này, chúng ta cần giải hệ phương trình trên. Đầu tiên, chúng ta sẽ giải phương trình f(x) = q(x) * (x - 2) + 7 để tìm giá trị của q(x). Sau đó, chúng ta sẽ thay giá trị của q(x) vào phương trình f(x) = p(x) * (x^2 + 1) + (3x + 5) để tìm giá trị của p(x) và r(x). Nhưng trước tiên, chúng ta cần biết đa thức f(x) là gì. Bạn có thể cung cấp thông tin về đa thức f(x) không?