tìm x , y thỏa mãn
2x+57=y2
Những câu hỏi liên quan
Tìm x,y thỏa mãn 3x2+y2+2x-2y-1=0 và 2x(x+y)=2 ai tich x,y hộ mik với
\(3x^2+y^2+2x-2y-1=0\)
\(\Leftrightarrow x^2+2x\left(x+y\right)-2xy+y^2+2x-2y-1=0\)
\(\Leftrightarrow x^2+2-2xy+y^2+2x-2y-1=0\)
\(\Leftrightarrow\left(x-y\right)^2+2\left(x-y\right)+1=0\)
\(\Leftrightarrow\left(x-y+1\right)^2=0\)
\(\Leftrightarrow x-y+1=0\)
\(\Leftrightarrow y=x+1\)
Thế vào \(x\left(x+y\right)=1\)
\(\Rightarrow x\left(2x+1\right)=1\)
\(\Leftrightarrow2x^2+x-1=0\Rightarrow\left[{}\begin{matrix}x=-1\Rightarrow y=0\\x=\dfrac{1}{2}\Rightarrow y=\dfrac{3}{2}\end{matrix}\right.\)
Đúng 3
Bình luận (0)
tìm số nguyên x,y thỏa mãn
x2-2x+y2+4y-4<0
\(x^2-2x+y^2+4y-4< 0\)
⇔ \(\left(x-1\right)^2+\left(y+2\right)^2< 9\)
Mà \(\left(x-1\right)^2\ge0;\left(y+2\right)^2\ge0\) và 2 số này đều là bình phương của một số nguyên
Nên ta có các trường hơpj
TH1 : \(\left\{{}\begin{matrix}\left(x-1\right)^2=0\\\left(y+2\right)^2=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\) (TM)
TH2 : \(\left\{{}\begin{matrix}\left(x-1\right)^2=1\\\left(y+2\right)^2=1\end{matrix}\right.\) .....
TH3 : \(\left\{{}\begin{matrix}\left(x-1\right)^2=4\\\left(y+2\right)^2=1\end{matrix}\right.\) .....
Thôi tự túc mấy trường hợp còn lại. Nghi đề sai lắm :((
Đúng 1
Bình luận (2)
⇔ \(\left(x-1\right)^2+\left(y+2\right)^2< 1\)
Mà \(\left(x-1\right)^2;\left(y+2\right)^2\ge0\forall x;y\) 2 số này đều là bình phương của một số nguyên
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)^2=0\\\left(y+2\right)^2=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Bài 3*: Tìm các cặp số nguyên (x;y) thỏa mãn xy2 + 2x – y2 =
Bài 3*: Tìm các cặp số nguyên (x;y) thỏa mãn xy2 + 2x – y2 =8
Lời giải:
$xy^2+2x-y^2=8$
$(xy^2-y^2)+(2x-2)=6$
$y^2(x-1)+2(x-1)=6$
$(y^2+2)(x-1)=6$
Vì $y^2+2\geq 0+2=2$ và $y^2+2, x-1$ là các số nguyên nên ta có bảng sau:
Đúng 0
Bình luận (0)
Cho x; y 0 thỏa mãn log 2x+ log2ylog4(x+y) Tìm x; y để biểu thức P x2+y2 đạt giá trị nhỏ nhất. A.
x
y
2
3
B.
x
2
3
;
y
2
C. xy1 D.
y
2
3
;
x
2
2
3
Đọc tiếp
Cho x; y> 0 thỏa mãn log 2x+ log2y=log4(x+y) Tìm x; y để biểu thức P= x2+y2 đạt giá trị nhỏ nhất.
A. x = y = 2 3
B. x = 2 3 ; y = 2
C. x=y=1
D. y = 2 3 ; x = 2 2 3
Theo đầu bài ta có: log 2x+ log2y=log4(x+y) hay 2 log 2(xy) =log2(x+y)
Suy ra x+y=(xy) 2
Đặt u= x+ y; v= xy ta có điều kiện u2-4v≥0; u>0; v>0 .
Mà 
Ta có
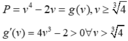
nên minP=
2
4
3
khi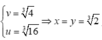 
Chọn A.
Đúng 0
Bình luận (0)
Trong tất cả các cặp (x;y) thỏa mãn
log
x
2
+
y
2
+
2
4
x
+
4
y
-
4
≥
1
. Tìm m để tồn tại duy nhất cặp (x;y) sao cho
x...
Đọc tiếp
Trong tất cả các cặp (x;y) thỏa mãn log x 2 + y 2 + 2 4 x + 4 y - 4 ≥ 1 . Tìm m để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0 .
A. 10 - 2 2
B. 10 - 2 h o ặ c 10 + 2
C. 10 - 2 2 h o ặ c 10 + 2 2
D. 10 - 2
Chọn C.
Phương pháp: Đưa bài toán về tìm m để hệ có nghiệm duy nhất.
Đúng 0
Bình luận (0)
Trong tất cả các cặp (x;y) thỏa mãn
log
x
2
+
y
2
+
2
2
x
-
4
y
+
6
≥
1
, tìm m để tồn tại duy nhất cặp (x;y) sao cho
x...
Đọc tiếp
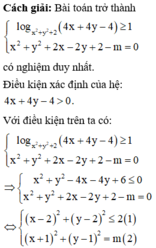
Trong tất cả các cặp (x;y) thỏa mãn log x 2 + y 2 + 2 2 x - 4 y + 6 ≥ 1 , tìm m để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0 .
A. 13 - 3 v à 13 + 3
B. 13 - 3
C. 13 - 3 2
D. 13 - 3 2 và 13 + 3 2
Trong tất cả các cặp (x;y) thỏa mãn
l
o
g
x
2
+
y
2
+
2
4
x
+
4
y
-
4
≥
1
Tìm m để tồn tại duy nhất cặp (x;y) sao cho...
Đọc tiếp
Trong tất cả các cặp (x;y) thỏa mãn l o g x 2 + y 2 + 2 4 x + 4 y - 4 ≥ 1 Tìm m để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0 .
Trong tất cả các cặp (x;y) thỏa mãn
log
x
2
+
y
2
+
2
4
x
+
4
y
-
4
≥
1
. Tìm m n...
Đọc tiếp
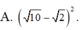
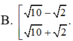
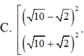
Trong tất cả các cặp (x;y) thỏa mãn log x 2 + y 2 + 2 4 x + 4 y - 4 ≥ 1 . Tìm m nhỏ nhất để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0 .
A. 10 - 2 2
B. 10 + 2
C. 10 + 2 2
D. 10 - 2
log x 2 + y 2 + 2 4 x + 4 y - 4 ≥ 1
⇔ 4 x + 4 y - 4 ≥ x 2 + y 2 + 2 ⇔ x - 2 2 + y - 2 2 ≤ 2
Đây là tập hợp tất cả các điểm nằm trên và trong đường tròn tâm I(2;2) bán kính ℝ ' = m .
Ta có I I ' = 10 . m nhỏ nhất để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0 thì hai đường tròn nói trên tiếp xúc ngoài
⇒ R + R ' = I I ' ⇔ m + 2 = 10 ⇔ m = 10 - 2 2
Đáp án cần chọn là B
Đúng 0
Bình luận (0)
Trong tất cả các cặp (x;y) thỏa mãn
log
x
2
+
y
2
+
2
4
x
+
4
y
-
4
≥
1
. Tìm m nhỏ nhất để tồn tại duy nhất cặp (x;y) sao cho...
Đọc tiếp
Trong tất cả các cặp (x;y) thỏa mãn log x 2 + y 2 + 2 4 x + 4 y - 4 ≥ 1 . Tìm m nhỏ nhất để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0
A. 10 - 2 2
B. 10 + 2
C. 10 + 2 2
D. 10 - 2