trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC với đường cao AH có phương trình:3x+4y+10=0 và đường phân giác trong BE có phương trình:x-y+1=0. điểm M(0;2) thuộc đường thẳng AB và cách đỉnh C một khoảng bằng \(\sqrt{2}\) Tính diện tích tam giác ABC

Những câu hỏi liên quan
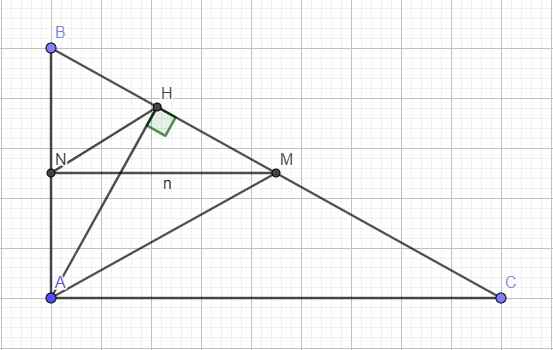
Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có đường cao AH : 3x-y+8=0 và đường trung tuyến AM: 3x+y-2=0 . Biết H, M thuộc BC ,\(\widehat{BAH}=\widehat{MAC}\) và \(BC=3\sqrt{10}\) . Viết phương trình tổng quát của đường thẳng BC.
trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC cân tại a. đường thẳng BC và đường cao kẻ từ B lần lượt có phương trình x+y+1=0, x-2y -2=0, điểm M (2,1) thuộc đường cao kẻ từ C. Xác định tọa độ các đỉnh tam giác ABC
Tọa độ B là nghiệm: \(\left\{{}\begin{matrix}x+y+1=0\\x-2y-2=0\end{matrix}\right.\) \(\Rightarrow B\left(0;-1\right)\)
Gọi vtpt của đường thẳng CM (cũng là đường cao kẻ từ C) có tọa độ \(\left(a;b\right)\)
H là chân đường cao kẻ từ B
\(cos\widehat{HBC}=\dfrac{\left|1.1+1.\left(-2\right)\right|}{\sqrt{1^2+1^2}.\sqrt{1^2+\left(-2\right)^2}}=\dfrac{1}{\sqrt{10}}\)
\(\Rightarrow cos\widehat{MCB}=cos\widehat{HBC}=\dfrac{1}{\sqrt{10}}=\dfrac{\left|a+b\right|}{\sqrt{a^2+b^2}.\sqrt{1^2+1^2}}\)
\(\Leftrightarrow\sqrt{a^2+b^2}=\sqrt{5}\left|a+b\right|\Leftrightarrow a^2+b^2=5\left(a+b\right)^2\)
\(\Leftrightarrow2a^2+5ab+2b^2=0\Leftrightarrow\left(a+2b\right)\left(2a+b\right)=0\)
Chọn \(\left(a;b\right)=\left[{}\begin{matrix}\left(2;-1\right)\\\left(1;-2\right)\end{matrix}\right.\) (trường hợp (1;-2) loại do song song BH)
\(\Rightarrow\) Phương trình đường cao kẻ từ C:
\(2\left(x-2\right)-1\left(y-1\right)=0\Leftrightarrow2x-y-3=0\)
Tọa độ C là nghiệm: \(\left\{{}\begin{matrix}x+y+1=0\\2x-y-3=0\end{matrix}\right.\) \(\Rightarrow C\left(...\right)\)
Gọi N là trung điểm BC \(\Rightarrow\) tọa độ N
Tam giác ABC cân tại A \(\Rightarrow\) AN là trung tuyến đồng thời là đường cao
\(\Rightarrow\) Đường thẳng AN vuông góc BC \(\Rightarrow\) nhận (1;-1) là 1 vtpt và đi qua N
\(\Rightarrow\) Phương trình AN
Đường thẳng AB vuông góc CM nên nhận (1;2) là 1 vtpt
\(\Rightarrow\) Phương trình AB (đi qua B và biết vtpt)
\(\Rightarrow\) Tọa độ A là giao điểm AB và AN
Đúng 1
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có M(2;0) là trung điểm của cạnh AB. Đường trung tuyến và đường cao qua đỉnh A lần lượt có phương trình là 7x-2y-3=0 và 6x-y-4=0. Phương trình đường thẳng AC là:
A.3x-4y-5=0
B.3x+4y+5=0
C.3x-4y+5=0
D.3x+4y-5=0
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có
M
(
2
;
0
)
là trung điểm của cạnh AB. Đường trung tuyến và đường cao qua đỉnh A lần lượt có phương trình là
7
x
-
2
y
-
3
0
và
6
x
-
y
-
4
0
. Phương trình đường thẳng AC...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có M ( 2 ; 0 ) là trung điểm của cạnh AB. Đường trung tuyến và đường cao qua đỉnh A lần lượt có phương trình là 7 x - 2 y - 3 = 0 và 6 x - y - 4 = 0 . Phương trình đường thẳng AC là
A. 3 x - 4 y - 5 = 0
B. 3 x + 4 y + 5 = 0
C. 3 x - 4 y + 5 = 0
D. 3 x + 4 y - 5 = 0
trong mặt phẳng với hệ trục tọa đọ oxy, cho tam giác ABC có phương trình đường cao kẽ từ A, đường phân giác trong kẽ từ C, trung tuyến kẽ từ B lần lượ là d1: 3x - 4y + 27= 0; d2: x +2y-5=0; d3:4x+5y-3=0. Tìm tọa dộ tâm và tính bán kính của của đường tròn ngoại tiếp tam giác ABC
1. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có cạnh AC đi qua điểm M (0;-1). Biết AB 2AM, phương trình đường phân giác trong AD : x-y 0, phương trìn đường cao CH: 2x+y+3 0. Tìm tọa độ các đỉnh A,B,C.2. Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD tâm I (-1;1). Gọi M nằm trên cạnh CD sao cho MC 2 MD. Tìm tọa độ điểm C biết đường thẳng AM có phương trình 2x-y0,điểm A có hoành độ dương
Đọc tiếp
1. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có cạnh AC đi qua điểm M (0;-1). Biết AB =2AM, phương trình đường phân giác trong AD : x-y =0, phương trìn đường cao CH: 2x+y+3 =0. Tìm tọa độ các đỉnh A,B,C.
2. Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD tâm I (-1;1). Gọi M nằm trên cạnh CD sao cho MC =2 MD. Tìm tọa độ điểm C biết đường thẳng AM có phương trình 2x-y=0,điểm A có hoành độ dương
trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC cân tại A, có trọng tâm g(4/3;1/3). Phương trình đường thẳng BC là x-2y-4=0, phương trình đường thẳng BG là 7x-4y-8=0. Tìm tọa độ các đỉnh của tam giác ABC
Trong mặt phẳng với hệ tọa độ Oxy , cho \(_{\Delta ABC}\) có đường cao AH : 3x-y+8=0 , trung tuyến AM: 3x+y-2=0 biết H,M thuộc đoạn BC , \(\widehat{BAH}=\widehat{MAC}\) và \(BC=3\sqrt{10}\) .Viết phương trình tổng quát của đường thẳng BC
Gọi N là trung điểm AB
Trong tam giác vuông ABH, HN là trung tuyến ứng với cạnh huyền
\(\Rightarrow HN=\dfrac{1}{2}AB=AN\Rightarrow\Delta AHN\) cân tại N
\(\Rightarrow\widehat{BAH}=\widehat{AHN}=\widehat{MAC}\) (1)
Trong tam giác ABC, MN là đường trung bình \(\Rightarrow MN||AC\) (2)
\(\Rightarrow\widehat{NMA}=\widehat{MAC}\) (3)
(1);(3) \(\Rightarrow\widehat{AHN}=\widehat{NMA}\) \(\Rightarrow\) tứ giác AMHN nội tiếp
\(\Rightarrow\widehat{ANM}=\widehat{AHM}=90^0\) (cùng chắn AM) hay \(MN\perp AB\) (4)
(2);(4) \(\Rightarrow AB\perp AC\) hay tam giác ABC vuông tại A
Tọa độ A là nghiệm: \(\left\{{}\begin{matrix}3x-y+8=0\\3x+y-2=0\end{matrix}\right.\) \(\Rightarrow A\left(-1;5\right)\)
AM là trung tuyến ứng với cạnh huyền trong tam giác vuông
\(\Rightarrow AM=\dfrac{1}{2}BC=\dfrac{3\sqrt{10}}{2}\)
Từ vecto pháp tuyến của AM và AM ta có:
\(cos\widehat{HAM}=\dfrac{\left|3.3-1.1\right|}{\sqrt{3^2+\left(-1\right)^2}.\sqrt{3^2+1^2}}=\dfrac{4}{5}\)
\(\Rightarrow AH=AM.cos\widehat{HAM}=\dfrac{6\sqrt{10}}{5}\)
Do H thuộc AH nên tọa độ có dạng: \(H\left(a;3a+8\right)\Rightarrow\overrightarrow{AH}=\left(a+1;3a+3\right)\)
\(\Rightarrow\left(a+1\right)^2+\left(3a+3\right)^2=\left(\dfrac{6\sqrt{10}}{5}\right)^2\)
\(\Rightarrow\) Giải ra a \(\Rightarrow\) tọa độ H \(\Rightarrow\) phương trình BC qua H và vuông góc AH nên nhận \(\left(1;3\right)\) là 1 vtpt
Đúng 1
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có trực tâm H(2;3) và phương trình đường tròn đi qua chân các đường cao của tam giác ABC có phương trình (C): x2 + y2 - 4x - 4y +1 =0. Viết phương trình đường tròn ngoại tiếp tam giác ABC
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có C(4;-1), đường cao, trung tuyến kẻ từ đỉnh A có phương trình lần lượt là d1: 2x-3y+12=0, d2: 2x+3y=0. Tìm tọa độ điểm B.
Tọa độ A là:
2x-3y+12=0 và 2x+3y=0
=>x=-3 và y=2
Tọa độ M, M là trung điểm của BC là M(x;-3x/2)
Phương trình BC sẽ là: 3x+2y+c=0
Thay x=4 và y=-1 vào BC, ta được:
3*4+2*(-1)+c=0
=>c+12-2=0
=>c=-10
=>BC: 3x+2y-10=0
=>B(x;5-1,5x); y=5-1,5x
B(x;5-1,5x); C(4;-1); M(x;-3x/2)
Theo đề, ta có: x=(4+x)/2 và -1,5x=(5x-1)/2
=>2x=x+4 và -3x=5x-1
=>x=4 và -8x=-1(loại)
=>Không có điểm B nào thỏa mãn
Đúng 1
Bình luận (0)