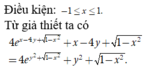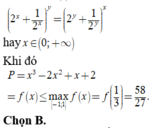Tìm x, y nguyên thỏa mãn: x4+y+4=y2-x2

Những câu hỏi liên quan
Tìm các số nguyên x, y thỏa mãn x 4 + x 2 − y 2 − y + 20 = 0. (1)
Ta có (1) ⇔ x 4 + x 2 + 20 = y 2 + y
Ta thấy: x 4 + x 2 < x 4 + x 2 + 20 ≤ x 4 + x 2 + 20 + 8 x 2 ⇔ x 2 ( x 2 + 1 ) < y ( y + 1 ) ≤ ( x 2 + 4 ) ( x 2 + 5 )
Vì x, y ∈ Z nên ta xét các trường hợp sau
+ TH1. y ( y + 1 ) = ( x 2 + 1 ) ( x 2 + 2 ) ⇔ x 4 + x 2 + 20 = x 4 + 3 x 2 + 2 ⇔ 2 x 2 = 18 ⇔ x 2 = 9 ⇔ x = ± 3
Với x 2 = 9 ⇒ y 2 + y = 9 2 + 9 + 20 ⇔ y 2 + y − 110 = 0 ⇔ y = 10 ; y = − 11 ( t . m )
+ TH2 y ( y + 1 ) = ( x 2 + 2 ) ( x 2 + 3 ) ⇔ x 4 + x 2 + 20 = x 4 + 5 x 2 + 6 ⇔ 4 x 2 = 14 ⇔ x 2 = 7 2 ( l o ạ i )
+ TH3: y ( y + 1 ) = ( x 2 + 3 ) ( x 2 + 4 ) ⇔ 6 x 2 = 8 ⇔ x 2 = 4 3 ( l o ạ i )
+ TH4: y ( y + 1 ) = ( x 2 + 4 ) ( x 2 + 5 ) ⇔ 8 x 2 = 0 ⇔ x 2 = 0 ⇔ x = 0
Với x 2 = 0 ta có y 2 + y = 20 ⇔ y 2 + y − 20 = 0 ⇔ y = − 5 ; y = 4
Vậy PT đã cho có nghiệm nguyên (x;y) là :
(3;10), (3;-11), (-3; 10), (-3;-11), (0; -5), (0;4).
Đúng 0
Bình luận (0)
tìm các số nguyên x,y thỏa mãn y2+3y=x4+x2+18
\(\Leftrightarrow\)\(4y^2+12y=4x^4+4x^2+72\)
\(\Leftrightarrow\left(2y+3\right)^2=\left(2x^2+1\right)^2+80\)
\(\Leftrightarrow\left(2y+3\right)^2-\left(2x^2+1\right)^2=80\)
\(\Leftrightarrow\left(2y+3-2x^2-1\right)\left(2y+3+2x^2+1\right)=80\)
\(\Leftrightarrow\left(y-x^2+1\right)\left(y+x^2+2\right)=20\)
Do \(x,y\in Z\) => \(y+1-x^2;y+x^2+2\in Z\)
=>\(y+1-x^2;y+x^2+2\inƯ\left(20\right)\)
Kẻ bảng làm nốt nha.
Đúng 2
Bình luận (0)
tìm số nguyên x,y thỏa mãn
x2-2x+y2+4y-4<0
\(x^2-2x+y^2+4y-4< 0\)
⇔ \(\left(x-1\right)^2+\left(y+2\right)^2< 9\)
Mà \(\left(x-1\right)^2\ge0;\left(y+2\right)^2\ge0\) và 2 số này đều là bình phương của một số nguyên
Nên ta có các trường hơpj
TH1 : \(\left\{{}\begin{matrix}\left(x-1\right)^2=0\\\left(y+2\right)^2=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\) (TM)
TH2 : \(\left\{{}\begin{matrix}\left(x-1\right)^2=1\\\left(y+2\right)^2=1\end{matrix}\right.\) .....
TH3 : \(\left\{{}\begin{matrix}\left(x-1\right)^2=4\\\left(y+2\right)^2=1\end{matrix}\right.\) .....
Thôi tự túc mấy trường hợp còn lại. Nghi đề sai lắm :((
Đúng 1
Bình luận (2)
⇔ \(\left(x-1\right)^2+\left(y+2\right)^2< 1\)
Mà \(\left(x-1\right)^2;\left(y+2\right)^2\ge0\forall x;y\) 2 số này đều là bình phương của một số nguyên
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)^2=0\\\left(y+2\right)^2=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Tìm cặp số nguyên x,y thỏa mãn : x2 + 4y2 = x2 y2 \(-\) 2xy
\(x^2+4y^2=x^2y^2-2xy\)
\(\Rightarrow x^2+4y^2+4xy=x^2y^2+2xy+1-1\)
\(\Rightarrow\left(x+2y\right)^2=\left(xy+1\right)^2-1\)
\(\Rightarrow\left(xy+1\right)^2-\left(x+2y\right)^2=1\)
\(\Rightarrow\left(xy-x-2y+1\right)\left(xy+x+2y+1\right)=1\)
Vì x,y là các số nguyên nên \(\left(xy-x-2y+1\right),\left(xy+x+2y+1\right)\) là các ước số của 1. Do đó ta có 2 trường hợp:
TH1: \(\left\{{}\begin{matrix}xy-x-2y+1=1\\xy+x+2y+1=1\left(1\right)\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}-xy+x+2y-1=-1\\xy+x+2y+1=1\end{matrix}\right.\)
\(\Rightarrow2\left(x+2y\right)=0\Rightarrow x=-2y\)
Thay vào (1) ta được:
\(-2y^2+1=1\Leftrightarrow y=0\Rightarrow x=0\)
TH2: \(\left\{{}\begin{matrix}xy-x-2y+1=-1\\xy+x+2y+1=-1\left(1\right)\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}-xy+x+2y-1=1\\xy+x+2y+1=-1\end{matrix}\right.\)
\(\Rightarrow2\left(x+2y\right)=0\Rightarrow x=-2y\)
Thay vào (1) ta được:
\(-2y^2+1=-1\Leftrightarrow\left[{}\begin{matrix}y=1\\y=-1\end{matrix}\right.\)
\(y=1\Rightarrow x=-2;y=-1\Rightarrow x=2\)
Vậy các cặp số nguyên (x;y) thỏa điều kiện ở đề bài là \(\left(0;0\right),\left(2;-1\right)\left(-2;1\right)\)
Đúng 2
Bình luận (0)
Tìm tất cả các số nguyên x, y thỏa mãn x2+y2+xy-x-y=1
Tìm số nguyên dương x, y thỏa mãn:
2019 . x2 + y2 = 2023
2019.\(x^2\) + y2 = 2023
Dùng phương pháp đánh giá tìm nghiệm nguyên em nhé.
Vì \(x\), y \(\in\) Z+ => \(x\); y ≥ 1
Với \(x\) = 1; y = 1 => 2019.12 + 12 = 2020 (loại)
Với \(x\) = 1; y = 2 => 2019.12 + 22 = 2023 ( thỏa mãn)
Với \(x\) > 1; y > 2 => 2019.\(x\) + y > 2019.12 + 22 = 2023
Vậy \(x\) = 1; y = 2 là nghiệm nguyên duy nhất thỏa mãn đề bài.
Kết luận: (\(x\); y) =( 1; 2)
Đúng 0
Bình luận (0)
tìm các cặp số nguyên x, y thỏa mãn: y2(x2-x+1)+xy = 3x-1
tìm các cặp số nguyên (x,y) thỏa mãn phương trình sau : x2 - y2= 2017
\(\Leftrightarrow\left(x-y\right)\left(x+y\right)=2017=1.2017\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-y=1\\x+y=2017\end{matrix}\right.\\\left\{{}\begin{matrix}x-y=-1\\x+y=-2017\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=1009\\y=1008\end{matrix}\right.\\\left\{{}\begin{matrix}x=-1009\\y=-1008\end{matrix}\right.\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Cho 2 hai số thực x, y thỏa mãn
e
x
-
4
y
+
1
-
x
2
-
e
y
2
+
1
-
x...
Đọc tiếp
Cho 2 hai số thực x, y thỏa mãn e x - 4 y + 1 - x 2 - e y 2 + 1 - x 2 - y = y 2 - x 4 . Giá trị lớn nhất của biểu thức P = x 3 + 2 y 2 - 2 x 2 + 8 y - x + 2 bằng
A. 2
B. 58 27
C. 115 27
D. 122 27
Tìm tất cả các cặp số nguyên dương (xy) thỏa mãn x2+y2-2(x+y) = xy
\(x^2+y^2+2\left(x+y\right)-xy=0\)
\(\Leftrightarrow4x^2-4xy+4y^2+8\left(x+y\right)=0\)
\(\Leftrightarrow\left(2x-y\right)^2+4\left(2x-y\right)+4+3y^2+12y+12=-16\)
\(\Leftrightarrow\left(2x-y+2\right)^2+3\left(y+2\right)^2=-16\)
Dễ thấy VT \(\ge0\) ; VP < 0 nên phương trình vô nghiệm
Đúng 2
Bình luận (0)
\(x^2+y^2-2\left(x+y\right)=xy\)
\(\Rightarrow x^2-2x+1+y^2-2y+1=2+xy\)
\(\Rightarrow\left(x-1\right)^2+\left(y-1\right)^2=2+xy\)
Ta lại có : \(\left(x-1\right)^2+\left(y-1\right)^2\ge2\left(x-1\right)\left(y-1\right)\) (Bất đẳng thức Cauchy)
Đúng 1
Bình luận (0)
Tiếp tục phần tiếp theo
Dấu bằng xảy ra khi \(\left\{{}\begin{matrix}x=2\\y=2\end{matrix}\right.\)
\(\Rightarrow\left(x-1\right)^2+\left(y-1\right)^2=2+xy\) (vô lý vì 2=2+2.2)
⇒ Không có cặp (x;y) nguyên dương nào thỏa mãn đề bài
Đúng 1
Bình luận (0)