trong mặt phẳng với hệ trục tọa độ Oxy, cho tam giác ABC với A(1;2), B(-3;4), C(3;0) M là trung điểm của BC, G là trọng tâm của tam giác ABC
a) Tìm tọa độ G, \(\overrightarrow{GM}\)
b)Tìm tọa độ điểm D sao cho tứ giác BGCH là hình bình hành
Trong không gian với hệ tọa độ O x y z , cho tam giác ABC có đỉnh C - 2 ; 2 ; 2 và trọng tâm G - 1 ; 2 ; 2 . Tìm tọa độ các đỉnh A, B của tam giác ABC, biết A thuộc mặt phẳng (Oxy) và điểm B thuộc trục cao.
A. A(-1;-1;0), B(0;0;4)
B. A(-1;1;0), B(0;0;4)
C. A(-1;0;1), B(0;0;4)
D. A(-4;4;0), B(0;0;1)
Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC vuông tại A(2;1);điểm B nằm trên trục hoành,điểm C nằm trên trục tung sao cho các điểm B,C có tọa độ không âm.Tìm tọa độ các điểm B;C sao cho tam giác ABC có diện tích lớn nhất.
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(-2;4), B(4;1), C(-2;-1). Tìm tọa độ trực tâm H tam giác.
vecto AH=(x+2;y-4); vecto BC=(-6;-2)
vecto BH=(x-4;y-1); vecto AC=(0;-5)
Theo đề, ta có: -6(x+2)-2(y-4)=0 và 0(x-4)-5(y-1)=0
=>y=1 và -6(x+2)=2(y-4)=2*(1-4)=-6
=>x+2=1 và y=1
=>x=-1 và y=1
Trong mặt phẳng với hệ trục tọa độ Descarter vuông góc Oxy, cho tam giác ABC vuông tại A với B(-3;0) và C(7;0) , bán kính đường tròn nội tiếp tam giác là r= 2√10 -5. Tìm tọa độ tâm I của đường tròn nội tiếp tam giác ABC, biết I có tung độ dương.
Trong mặt phẳng với hệ trục tọa độ Descarter vuông góc Oxy, cho tam giác ABC vuông tại A với B(-3;0) và C(7;0) , bán kính đường tròn nội tiếp tam giác là r=2√10-5
. Tìm tọa độ tâm I của đường tròn nội tiếp tam giác ABC, biết I có tung độ dương.
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với và . a) Tính tọa độ điểm G và vectơ ( với điểm G là trọng tâm tam giác ABC ). b) Tìm tọa độ điểm D là giao điểm của đường thẳng BC với trục hoành.
Đề thiếu hết dữ liệu tọa độ các điểm rồi bạn
Trong mặt phẳng với hệ tọa độ vuông góc Oxy cho điểm M(-1;1). Viết phương trình đường thẳng qua M và tạo với hai trục tọa độ một tam giác vuông cân.
Trong mặt phẳng với hệ tọa độ vuông góc Oxy cho điểm M(-1;1). Viết phương trình đường thẳng qua M và tạo với hai trục tọa độ một tam giác vuông cân.
gọi Pt đường thảng .....y=ax+b(d)
d đi qua M(-1,1) 1=-a+b⇔b=a+1
gọi d cắt Ox tại \(A\left(-\dfrac{b}{a},O\right)\)
d cắt Oy tại \(B\left(O,b\right)\)
\(\Delta AOB\) vuông cân tại o
\(\Rightarrow OA=OB\Rightarrow\left(-\dfrac{b}{a}\right)^2+o^2=o^2+b^2\)
\(\dfrac{b^2}{a^2}=b^2\Leftrightarrow\dfrac{1}{a^2}=1\Leftrightarrow a^2=1\)
\(\Leftrightarrow\left[{}\begin{matrix}a=1\\a=-1\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}b=2\\b=0\left(loại\right)\end{matrix}\right.\)
(do d cắt 2 trục tọa độ nên a,b≠0)
vậy PtT đg thảng d:y=x+2
Gọi pt đường thẳng có dạng \(y=ax+b\)
Đường thẳng qua M tạo 2 trục tọa độ 1 tam giác vuông cân khi nó có hệ số góc \(a=1\) hoặc \(a=-1\)
\(\Rightarrow\left[{}\begin{matrix}y=x+b\\y=-x+b\end{matrix}\right.\)
Thay tọa độ M vào phương trình ta được:
\(\left[{}\begin{matrix}1=-1+b\\1=-\left(-1\right)+b\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}b=2\\b=0\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}y=x+2\\y=-x\end{matrix}\right.\)
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(2;-1), B(4;5) và C(-3;2). Lập phương trình đường cao của tam giác ABC kẻ từ A.
A. 7x + 3y - 11 = 0
B. -3x + 7y + 13 = 0
C. 3x + 7y + 1 = 0
D. 7x + 3y + 13 = 0
Chọn A.
Gọi AH là đường cao của tam giác ABC ⇒ AH ⊥ BC.
B(4;5), C(-3;2) 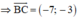
Phương trình đường cao AH đi qua A(2;-1) nhận 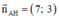 là VTPT là:
là VTPT là:
7.(x - 2) + 3.(y + 1) = 0 ⇔ 7x - 14 + 3y + 3 = 0 ⇔ 7x + 3y - 11 = 0
Vậy phương trình đường cao AH là 7x + 3y - 11 = 0.
Trong mặt phẳng hệ tọa độ oxy, cho tam giác ABC có đỉnh A nằm trên trục õ với 0<xa<2,5. Các đường cao xuất phát từ B và C lần lượt có pt d1:x-y+1=0 à d2:2x+y-4=0. Tìm tọa độ các đỉnh A,B,C sao cho diện tích tam giác ABC bằng 6,75